Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Рассмотрим двухмерный (композиционный) код, изображенный на рисунке 1.

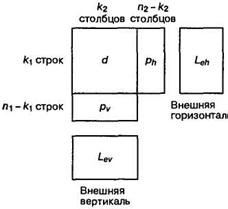
Рис. 1. Структура двухмерного композиционного кода

Структуру этого кода можно представить как массив данных, состоящий из k₁ строк и k₂ столбцов. В k₁ строках содержатся кодовые слова, образованные k₂ битами данных и п₂ - k₂ битами четности. Каждая из k₁ строк представляет собой кодовое слово кода (п₂, k₂). Аналогично k₂ столбцов содержат кодовые слова, образованные из k₁ бит данных и п₁ - k₁ бит четности. Таким образом, каждый из k₂ столбцов представляет собой кодовые слова кода (п₁, k₁). Обозначим различные участки массива следующим образом: d - для данных, p_h - для горизонтальной четности (вдоль строк) и p_v - для вертикальной четности (вдоль столбцов). Фактически получаем, что каждый блок битов данных размером , будет кодирован двумя кодами: горизонтальным и вертикальным.

На рисунке 1 присутствуют блоки L_eh и L_ev,, которые содержат значения внешних LLR. Они получены из горизонтального и вертикального кодов [1]. Код с коррекцией ошибок дает некоторое улучшение достоверности передачи. Внешние LLR представляют собой меру этого улучшения. Такой композиционный код является простым примером каскадного кода. Его структура описывается двумя отдельными этапами кодирования: горизонтальным и вертикальным.

Как показывает уравнение

                        (1)

решение при финальном декодировании каждого бита и его надежности зависит от значения . Опираясь на (1), можно записать алгоритм, дающий финальное  и внешние LLR (горизонтальное и вертикальное). Для композиционного кода алгоритм такого итеративного декодирования имеет следующий вид [2]:

1. Если априорные вероятности битов данных не равны, то устанавливается априорное LLR L(d) = 0.

2. Декодируется горизонтальный код и, на основе уравнения (1), вычисляется горизонтальное LLR.

3. Для этапа 4 вертикального декодирования устанавливается .

4. Декодируется вертикальный код и, на основе уравнения (1), вычисляется вертикальное LLR.

5. Для этапа 2 горизонтального декодирования устанавливается . Затем повторяются этапы 2 - 5.

6. После достаточного для получения надежного решения количества итераций следует перейти к этапу 7.

7. Мягким решением на выходе будет

.                   (2)

Рассмотрим пример, применения этого алгоритма к очень простому композиционному коду, т.е. двухмерному коду с одним разрядом контроля четности.

Пусть в кодере биты данных и биты контроля четности имеют значения, как показано на рисунке 2, а). Связь между битами данных и битами контроля четности внутри конкретной строки или столбца выражается через двоичные цифры 0 и 1 следующим образом:

                                     (3)

и

.                                 (4)

Рис. 2. Пример композиционного кода

Переданные биты представлены последовательностью d₁, d₂, d₃, d₄, p₁₂, p₃₄, p₁₃, p₂₄. На входе приемника биты, искаженные помехами, представляются последовательностью {х_i}, {х_ij}. В этой ситуации для каждого принятого бита данных x_i = d_i + n, для каждого принятого бита контроля четности , а n представляет собой распределение помех, которое статистически независимо от d_i и р_ij. Индексы i и j обозначают позицию в выходном массиве кодера, изображенном на рисунке 2, а). Чтобы было удобно будем также использовать обозначение принятой последовательности в виде {х_k}, где k является временным индексом. Оба типа обозначений будем рассматривать далее. Индексы i и j используются для позиционных отношений внутри композиционного кода, а k для более общих аспектов временной зависимости сигнала. Какое из обозначений должно быть заметно по контексту?

Если основываться на отношениях, установленных в уравнениях (11) - (14) [1], и считать модель каналом AWGN с помехами, LLR для канальных измерений сигнала х_k, принятого в момент k, имеет следующий вид:

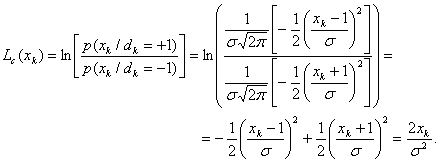                          (5)

Здесь применяется натуральный логарифм. Если помеха имеет дисперсию равную 1, то получим

.                               (6)

Пусть информационная последовательность d₁, d₂, d₃, d₄ образована двоичными числами 1 0 0 1, как показано на рисунке 2, а). Используя уравнение (3), получаем, что контрольная последовательность p₁₂, p₃₄, p₁₃, p₂₄ равна 1 1 1 1. Следовательно, переданная последовательность имеет следующий вид:

{d_i}, { р_ij} = 1 0 0 1 1 1 1 1.           (7)

Если информационные биты выражаются через значения биполярного электрического напряжения +1 и -1, соответствующие логическим двоичным уровням 1 и 0, то переданная последовательность будет следующей:

{d_i}, { р_ij} = +1, -1, -1, +1, +1, +1, +1, +1.

Допустим, что помехи преобразуют эту последовательность информации и контрольных данных в принятую последовательность

{х_i}, {х_ij} = 0.75, 0.05, 0.10, 0.15, 1.25, 1.0, 3.0, 0.5,                                                 (8)

где компоненты {х_i}, {х_ij} указывают переданную информацию и контрольные данные {d_i}, { р_ij}. Следуя позиционному описанию, принятую последовательность можно записать следующим образом:

{х_i}, {х_ij} = х₁, х₂, х₃, х₄, х₁₂, х₃₄, х₁₃, х₂₄.

Применяя уравнение (6) предполагаемые канальные измерения дают следующие значения LLR:

 = 1.5, 0.1, 0.20, 0.3, 2.5, 2.0, 6.0, 1.0.                       (9)

Эти величины показаны на рисунке 2, б) как входные измерения декодера. Заметим, что если принимаются жесткие решения на основе значений {х_k} или , при равной априорной вероятности переданных данных, то такой процесс должен в результате давать две ошибки, т.к. и d₂, и d₃ могут быть неправильно трактованы как двоичная 1.

Внешние функции правдоподобия

При выражении мягкого выхода для принятого сигнала, соответствующего данным d₁, в случае композиционного кода, изображенного на рисунке 2, используется уравнение  [1], так что

 L_c(x₁₂)}                                 (10)

где члены  L_c(x₁₂)} представляют внешнее LLR, распределенное кодом, т.е. прием соответствующих данных d₂ и их априорной вероятности совместно с приемом соответствующей четности p₁₂. В общем случае мягким выходом  для принятого сигнала, соответствующего данным d_i будет

 L_c(x_ij)}                       (11)

где L_c(x_i), L_c(x_j) и L_c(х_ij) - канальное измерение LLR приема соответствующих d_i, d_j и р_ij. L(d_i), L(d_j) - LLR для априорных вероятностей d_i и d_j,  L_c(x_ij)} - внешнее распределение LLR для кода. Уравнения (10) и (11) становятся понятнее при рассмотрении рисунка 2, б). Пусть происходит равновероятная передача сигнала. Тогда в этой ситуации мягкий выход  представляется измерением LLR детектора L_c(x₁) = l.5 для приема, соответствующего данным d₁ плюс внешнее LLR  L_c(x₁₂) = 2,5], получаемое в результате того, что данные d₂ и четность р₁₂ также дают сведения о данных d₁ как это показывают уравнения (3) и (4).

СПИСОК ЛИТЕРАТУРЫ:

1. Ташатов Н.Н. Турбокодирование и функции правдоподобия // В печати.
2. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. - Издательский дом «Вильямс», 2004. - 1104 с. ил.