Если система очень сложна - обладает большим числом степеней свободы, детерминированное описание теряет смысл. Случайность движения обычно ассоциируется с двумя обстоятельствами: с очень «чувствительной» зависимостью от начальных условий и с существованием средних по времени величин. Нас будут интересовать случаи, когда существует средняя величина:
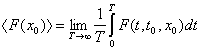, (1)
такая, что 
для большинства начальных условий в заданной области фазового пространства не зависит от x0 .
Перечислим фазовые траектории, которые могут существовать внутри области, из которой фазовые траектории не выходят: неустойчивые состояния равновесия, неустойчивые циклы и незамкнутые траектории, блуждающие внутри области. В консервативных системах существование временных средних (1) следует из эргодической теории динамических систем.
О степени стохастичности движения системы судят по скорости спадания автокорреляционной функции:
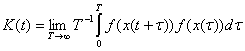. (2)
Присутствие в K(t) периодической или квазипериодической составляющей означает, что в движении есть периодические или квазипериодические компоненты (например, незамкнутая траектория на торе)(2). Развитая стохастичность приводит к тому, что функции f (x(t+
)) и f (x( )) быстро становятся независимыми, т.е. K(t) достаточно быстро стремится к нулю. Спектр реализации в этом случае - сплошной.
Если спадание K(t) экспоненциально, то говорят, что в системе есть перемешивание. Перемешивание есть несомненный признак стохастичности динамических систем [1,2]. Достаточно наглядно процесс перемешивания в фазовом пространстве можно представить следующим образом. Возьмем ансамбль траекторий с начальными условиями внутри маленького фазового объема - «капли фазовой жидкости». Пусть эта «капля» отличается по цвету от остальной жидкости внутри рассматриваемой области фазового пространства. Если в этой области есть, например , предельный цикл, то через некоторое время наша капля растянется вдоль предельного цикла и окрасит лишь узкий поясок в окрестности. Если же все траектории внутри ограниченной области неустойчивы, капля будет непрерывно растягиваться, приобретая все более сложную форму, и при t →∞ она более или менее равномерно окрасит всю область, т.е. перемешивается с неокрашенной жидкостью. Таким образом, в системе с неустойчивыми траекториями начальное распределение вероятностей стремится к некоторому установившемуся - инвариантному вероятностному распределению, которое и определяет статистические свойства стохастических движений детерминированной системы.
Будем говорить, что динамическая система является стохастической, если: 1) существует предельное распределение вероятностей в фазовом пространстве системы, которому стремится любое начальное неравновесное распределение; 2) поведение системы эргодично - среднее по времени для произвольной функции, заданной в фазовом пространстве, равно среднему по предельному (инвариантному ) распределению; 3) движение системы характеризуется сплошным спектром, т.е. спадающей автокорреляционной функцией.
В частности, будем пользоваться критерием стохастичности, в основе которого лежит определение величины h, характеризующей разбегание соседних траекторий в линейном приближении - если эта величина положительна, то движение стохастично ( энтропия Колмогорова - Синая). Математическим образом стохастического движения динамической системы является стохастическое множество траекторий в ее фазовом пространстве. Для гамильтоновых систем и диссипативных систем эти множества обладают различными свойствами.
Согласно теореме Лиувилля фазовая жидкость гамильтоновой системы несжимаема, т. е. начальный поток траекторий сохраняет свой объем в фазовом пространстве. В диссипативных системах ситуация иная - по определению фазовый объем в таких системах в среднем сжимается, т.е. в среднем по фазовому пространству div u < 0 ( u - векторное поле в фазовом пространстве ).
Таким образом, стохастическое множество в диссипативной системе - это замкнутое притягивающее множество траекторий, на котором все принадлежащие ему траектории неустойчивы. Такое множество называют странным аттрактором. Размерность странного аттрактора всегда меньше размерности фазового пространства.
СПИСОК ЛИТЕРАТУРЫ:
- Синай Я.Г. Стохастичность динамических систем. /Под ред. А.В. Гапонова. М.: изд-во «Наука». В кн.: Нелинейные волны.1979. С. 192 - 212.
- Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн./ М.: изд-во «Наука». 1984. С. 355 - 362.