Режим пакетной передачи данных в системах подвижной радиосвязи (СПР) играет существенную роль, особенно в последнее время, когда активно развиваются низкоорбитальные спутниковые системы, пакетные радиосети (включая транкинговые системы радиосвязи), сети мобильного беспроводного широкополосного радио доступа. В этих системах предполагается режим равного доступа любого из M абонентов системы к любому из L предоставляемых каналов, при этом, наряду с речевой передается служебная информация в виде отдельных пакетов данных. Для передачи данных в таких системах используется либо выделенный служебный канал, либо служебная информация передается по свободному информационному каналу.
В этой связи определение возможности обеспечения пакетной передачи данных в совмещенном радиоканале без увеличения очереди у абонентов системы, т.е. определение условий эргодичности процесса передачи информации определяет условия работоспособности системы.
Рассматриваемые системы представим в виде структуры. Каждый абонент системы имеет источник пакетов данных. Генерируемые источником пакеты предназначаются для передачи по освободившимся в данный момент каналам из общего числа L каналов. Все пакеты имеют одинаковую длину, которая принимается за единицу времени. Пакет помимо информационного блока содержит адресный блок, указывающий, от кого и кому предназначается передаваемая информация. Все время передачи дискретной информации разделено на единичные интервалы, равные длине пакета, называемые окнами. Длительность окна может быть выбрана из статистического оценивания времени, в течении которого радиоканал свободен от передачи аналоговой информации. Абоненты точно знают моменты разделения окон t=0,1,... (синхронный доступ) в каждом канале и число свободных каналов. Это обеспечивается передачей служебных команд от центральной станции (ЦС).
После передачи пакета абонент получает подтверждение от ЦС о трех возможных ситуациях в окне: пакет на данном канале не передавался (пустое окно канала), передавался один пакет в канале (успешная передача), одновременно передавались в канале два или более пакетов и произошло их наложение (конфликт). Помимо этого, каждый абонент получает от ЦС информацию о том, свободен канал для передачи пакетов в следующем окне или занимается под передачу аналоговой информации. В отличие от системы АЛОХА в данном случае передача пакетов осуществляется по l освободившимся каналам, т.е. каждый абонент получает «случайный доступ» в один из l освободившихся каналов.
Работа каждого источника не зависит от работы других источников, а также от всех других случайных событий в системе. Пакеты, производимые источниками, образуют вероятностные потоки, которые описываются следующим образом.
Пусть βm (t) - число пакетов, произведенных источником m-го абонента (m = 
) в течении окна (t-1,t). Величины {βm (t);t=0,1,2,...} считаются независимыми, одинаково распределенными случайными величинами, принимающими значения из множества {0,1,2,...}. Обозначим qm (k)=P{ βm =k}; 
(k)=1. Величины β1(t1),...,βm(tm) считаются статистически независимыми при любых t1,...,tm .
Запишем среднее и дисперсию числа пакетов, поступающих от m-го абонента в течение одного окна, в виде
У каждого абонента все готовые для передачи пакеты становятся в очередь. Если очередь пуста в момент начала окна t, то абонент в окне (t,t+1) ничего по каналу не передает (молчит). Если в момент t очередь у m-го абонента содержит nm(t) ≥ 1 пакетов, то независимо от всех других случайных событий в системе этот абонент с некоторой заданной вероятностью pm предпринимает попытку выйти на связь (передает пакет) и "молчит" с вероятностью 1 - pm. При этом он случайным образом с некоторой вероятностью pi попытается занять i-ый канал из l свободных, так, что 
= 1.
Таким образом, вероятность занятия i-го канала при непустой очереди у m-го абонента составит pm pi = pmi.
Первоначально будем считать, что l нам известно. Тогда рассматриваемую систему связи удобно описывать марковской моделью. Состоянием системы в момент t называется случайный вектор 
=( n1(t), n2(t),...,nM(t)), где ni(t) - длина очереди i-го абонента в момент t. Как функция t вектор образует M-мерную цепь Маркова с дискретным временем t=0,1,2,... и дискретным множеством состояний 
{
≥ целые}.
Вероятность перехода за один шаг цепи из состояния 
=( S1,....,SM) ∈
в состояние 
=(k1,....,kM )∈
= 
,
где
а 
-вероятность, зависящая от условной вероятности Pm(S) - вероятности успешной передачи пакета m-ой станции при условии, что (t) = и Sm> 0
Pm( ) = 
,
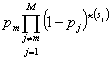где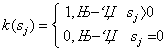 
Цепь обладает свойством ограниченной однородности по состояниям, является неприводимой и апериодической. Нетрудно показать, что для определения достаточных условий эргодичности цепи достаточно рассматривать одномерные цепи Маркова, каждая из которых описывает длину очереди у m-го абонента. Таким образом, если для каждого m=1,2,...,M определить однородную цепь Маркова ηm(t), t=1,2,..., с множеством состояний {1,2,...,} и вероятностями перехода за один шаг
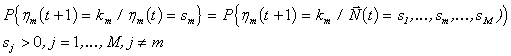
то справедлив результат
. (1)
Неравенство (1) определяет тот факт, что наихудшими условиями работы системы являются такие, при которых очереди непусты у всех M абонентов. Цепь ηm(t) описывает длину очереди m-го абонента в наихудших условиях.
Если обозначить 
- условную вероятность успешной передачи пакета m-м абонентом при наихудших условиях (очереди на всех станциях непустые), то можно воспользоваться достаточными условиями эргодичности n(t):
, m=1,2,...,M. (2)
Следует отметить, что условия, при которых доказывается справедливость (2), в рассматриваемой задаче выполняются. Таким образом, для определения достаточных условий на эргодичность необходимо определить .
Рассмотрим ситуацию, когда у всех абонентов очереди не пусты. Тогда условная вероятность успешной передачи пакета m-м абонентом
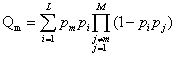, (3)
где 1-й член определяет выход m-го абонента в i-ый канал и его занятие при условии, что все остальные абоненты в этот канал не выйдут (2-ой член).
Существенный практический интерес представляет случай, когда все абоненты находятся в равных условиях (отсутствуют приоритеты) и все свободные каналы занимаются равновероятно
. (4)
Тогда, раскрывая (3), получаем 
.
Определим максимум по вероятности p - предпринятия попытки передачи пакета при фиксированном числе каналов l:
= (1-p/l)-(M-1)p/l = 0 (5)
Из (5) точка экстремума достигается при значении 
.
Таким образом
(6)
Поскольку l - случайная величина, определим среднее число свободных для пакетной передачи каналов.
Для системы с отказами справедливы соотношения:
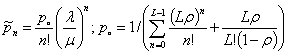(7)
где 
- вероятность освобождения n каналов от передачи аналоговой информации; λ,μ - интенсивности потока телефонных заявок и обслуживания; ρ = λ / Lμ.
Тогда среднее число каналов, которые могут быть использованы для пакетной передачи,
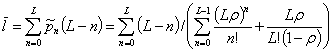. (8)
В этом случае условная вероятность успешной передачи пакета
. (9)
Из сравнения (9) и (6) видно, что одинаковую вероятность успешной передачи пакета можно обеспечить либо закреплением 
каналов, либо случайным доступом в освобождающиеся при =] 
[, где ] [ - ближайшее целое при 
.
Если рассматривать систему с одним закрепленным каналом для передачи пакетов (l =1), то (7) и (8) позволяют рассчитать параметры эквивалентной ей многоканальной системы, использующей режим уплотнения случайным образом освобождающихся каналов.
В связи с этим важно отметить, что достаточное условие (2) эргодичности цепи является сильно избыточным (очень осторожным), что наглядно иллюстрируется в [1] для M=2. Следовательно, и расчеты по (8), (9) дадут параметры многоканальной системы с большим запасом по пропускной способности.
Таким образом, в результате анализа дискретной марковской цепи , описывающей состояние рассматриваемой системы в режиме случайного множественного доступа при передаче пакетов данных, получены условия эргодичности с учетом многоканальности системы.