В последнее время в технике идет переход на цифровые методы обработки информации. Это связано с тем, что цифровую информацию легче хранить (появились дешевые и удобные устройства для хранения информации, такие как жесткие диски компьютеров или лазерные диски), а также с тем, что цифровую информацию легко передавать по современным линиям связи практически без потерь.
Аналоговый сигнал - это в простейшем случае функция x(t), зависящее от времени t. При записи на носитель информации или воспроизведении с него сигнал неизбежно искажается различного рода шумами. Восстановить искаженный сигнал (убрать шумы) нельзя. Можно, конечно, пытаться подавлять шумы, используя некоторую дополнительную информацию (например, можно подавлять частоты, в которых сосредоточены шумы), но при этом мы теряем также и информацию о самом сигнале, т.е. опять же вносим искажения.
При оцифровке сигнала x(t) производятся две операции - дискретизация и квантование. Дискретизация - это замена сигнала x(t) с непрерывным време-нем t на дискретизованный сигнал - последовательность чисел x(ti) для дискретного набора моментов времени t1, t2, ..., ti ..., (чаще всего интервалы между моментами времени Δt = ti - ti-1 берутся одинаковыми). При дискретизации, конечно, часть информации о сигнале теряется. Но если сигнал x(t) за время Δt не сильно изменяется, числа x(ti) и x(t)i-1 близки друг к другу, то поведение x(t) между временами ti и ti-1 нетрудно восстановить (сигнал практически линейно изменяется во времени от x(ti-1) до x(ti) ). При дискретизации мы теряем частотные составляющие сигнала с частотами порядка ![]() и выше.
и выше.
При дискретизации время из аналогового как бы становится цифровым - моменты времени ti можно нумеровать, кодировать. Производится замена непрерывного времени t на нечто, которое может принимать не все значения, а только некоторые, а именно t1, t2, ..., ti ... Квантование сигнала - это нечто похожее, только данная процедура производится не со временем, а со значением сигнала x. Выбирается некий набор возможных значение сигнала x1, x2, ..., xn ... и каждому x(ti) сопоставляется ближайшее число из этого набора.
При наличии априорной информации о функции, описывающей сигналы, обычно строится соответствующая этому закону последовательность интерполяционных полиномов по той или иной базисной системе, в узлах интерполяционного полинома устанавливаются датчики, а сам полином выбирается совпадающим в этих узлах со снятыми с датчиков значениями. Однако в многомерном случае требование совпадения в узлах во многих случаях неоправданно усложняет приближающую функцию, одновременно сужая возможности ее выбора. Поэтому часто отказываются от этого требования (фактически без потери информации, поскольку в узлах сетки информация и так известна) и, для того, чтобы подчеркнуть это обстоятельство, вместо термина «интерполяция» пользуются термином «восстановление».
Подобная задача подробно изучалась и сейчас интенсивно изучается многими математиками и инженерами [1].
Перейдем к постановке задачи восстановления сигналов, которая является переформулировкой задачи восстановления функций на языке теории сигналов и информации.
Пусть X и Y нормированные пространства числовых функций, описывающих сигналы и определенных соответственно на множествах Ω и Ω1. Пусть F (F ⊂ X) - класс функций, описывающий сигналы, и Tf = u(y; f) - есть отображение F в Y.
Для каждого целого положительного N выбирается набор l (N) = (l1, l2, ..., lN) , где lj(f):F→C (j = 1, 2, ..., N) - функционалы носители числовой информации о «полезном» сигнале f , и алгоритм
φN(z1, z2, ..., zN; y):CN×Ω1→C,
переработки полученной информации до «восстановленного» сигнала, и по которым строится последовательность алгоритмов восстановления сигнала
(TNf)(y) = φN(l1(f), l2(f), ..., lN(f); y).
Таким образом, при любом целом положительном N для каждого сигнала f∈F восстановление сигнала Tf = u(y; f) производится в метрике Y пос-редством алгоритма восстановления
(TNf)(y) = φN(l1(f), l2(f), ..., lN(f); y).
Пусть {l (N) } и {φN} - множества всевозможных наборов функционалов l (N) и алгоритмов φN соответственно, и пусть DN⊂ {l (N) } × { φN }, т.е. DN есть фиксированное множество пар (l (N) , {φN).
Положим
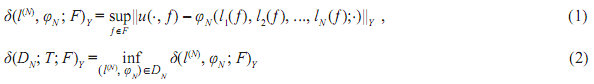
Задача заключается в получении оценок сверху и совпадающих с ними с точностью до констант или близких к ним оценок снизу величин (1) - (2), при различных их конкретизациях и построении алгоритмов φN , реализующих оценки сверху.
Конкретизируя в (1) и (2) операторы Т и множества DN (класс алгоритмов восстановления сигналов), пространства X и Y, классы сигналов F (F⊂X) получаем различные постановки задач.
Нами ниже рассматривается случай восстановления сигналов из классов Е и SW.
Дадим их определения.
1) Анизотропный класс Коробова Er1.....r5( c), Er1,...,r5(1) ≡ Er1,...,r5 (rj >1, j=1 ..., s) состоит из всех 1-периодических по каждой переменной функций ƒ(x) = ƒ(x , ..., xs), тригонометрические коэффициенты Фурье которых удовлетворяют условию
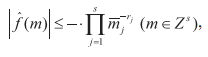
где здесь и всюду ниже полагается ![]()
2) Класс Соболева ![]() есть множество всех функций ƒ(x) = ƒ(x, ..., xs) пред-ставимых в виде свертки
есть множество всех функций ƒ(x) = ƒ(x, ..., xs) пред-ставимых в виде свертки
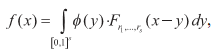
где
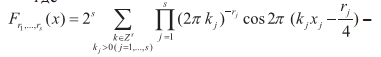
многомерные аналоги ядер Бернулли и ![]() .
.
Одним из авторов настоящей статьи [2] получен оператор восстановления функций многих переменных, который явным образом переносится на случай восстановления сигналов.
В [2] фактически построен алгоритм восстановления s-мерного сигнала f по его дискретизованному сигналу, т.е. последовательности чисел ƒ(ξ ( j )):
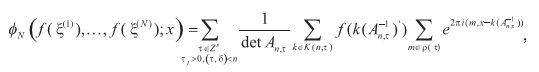
где
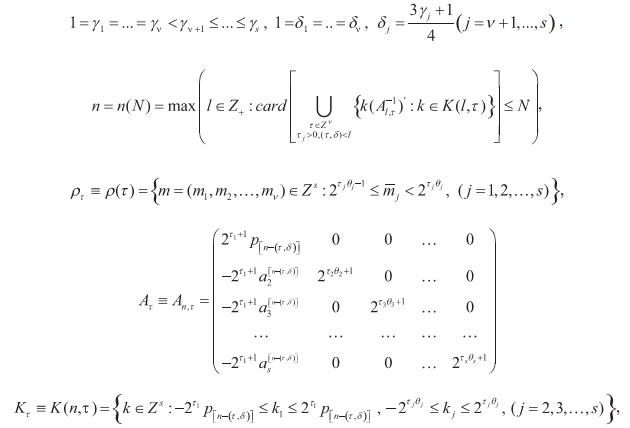
Здесь для каждого целого положительного l через pl обозначено простое число, удовлетворяющее соотношению
2l+3 ≤ pl < 2l+4.
Заметим, что такое число pl найдется всегда, поскольку для всякого действительного числа L>3 между L и 2L имеется простое число p (постулат Бертрана).
Замечание 1. Данный алгоритм восстановления сигнала используется в случае, когда сигнал имеет различные свойства по разным переменным (см. нижеприведенные теоремы 1 и 2). Данный алгоритм восстановления сигналов (функций), когда γ j = 1 (т.е. когда сигнал имеет одинаковые свойства по всем переменным), впервые построен и применен К.Е. Шерниязовым [3].
Замечание 2. Данный алгоритм восстановления сигналов дает неулучшаемые погрешности для периодических сигналов. Поэтому для его применения необходимо вначале периодизировать сигнал. Один из способов периодизации описан в [4].
В [2] доказана следующая теорема о восстановлении сигналов.
Теорема 1. Пусть 1 < r = r1 = r2 = ... = rn < rn+1 ≤ ... ≤ rs , где s (s = 2, 3, ...) целое положительное число. Тогда справедливо соотношение
![]()
для γj = rj / r1 ( j = 1,....,s), а класс F есть каждый из классов ![]()
Также в [2] доказана неулучшаемость погрешности восстановления сигналов при использовании любых линейных алгоритмов восстановления.
Теорема 2. Пусть 1 < r = r1 = r2 = ... = rn < rn+1 ≤... ≤ rs , где s (s = 2, 3, ...) целое положительное число. Тогда справедливо соотношение
![]()
где F есть каждый из классов ![]()
СПИСОК ЛИТЕРАТУРЫ:
- Темиргалиев Н. Теоретико-числовые методы и теоретико-вероятностный подход к задачам Анализа. Теория вложений и приближений, абсолютная сходимость и преобразования рядов Фурье. // Вестник Евразийского государственного университета. - 1997. -№3. - С.90-144. Продолжение 1. // Евразийского национального университета. - 2002. - № 3-4. - С.222-272.
- Ташатов Н.Н. Приближенное восстановление функций и решений уравнения Пуассона с правой частью из анизотропных классов Е и SW. Кандидатская диссертация. КарГУ им. Е.А. Букетова. - Караганда. - 2002.
- Шерниязов К.Е. Приближенное восстановление функций и решений уравнений с функциями распределения начальных температур из классов Е , SW и B. Кандидатская диссертация. КазГУ им. Аль-Фараби. - Алматы. - 1998.
- 4. Коробов Н.М. Теоретико-числовые методы в приближенном анализе. - М.: МЦНМО. - 2004. - 288с.



