Рассмотрим задачу многокритериальной оптимизации поэтапного планирования производства продукции на основе процессной модели.
Обозначим через t - время, причем t0 ≤ t ≤ tn, где tj = t0 + jΔtj - верхняя граница j-го (j = 1, 2, ..., n) временного этапа производства, Δtj - его продолжительность. В случае постоянного шага дискретизации процессов по времени Δtj ≡ Δt имеем tj = t0 + jΔt.
Введем X(t) - искомый план-график производства, кусочно-непрерывную функцию, принимающую для j-го временного этапа постоянное значение xj = X(tj) = const.
Пусть a(t) - динамический план-график выпуска продукции, обусловленный спросом или имеющимся портфелем заказов предприятия. Тогда между валовым объемом заказа и максимально возможным объемом производства S, обусловленным имеющимися мощностями, реализуется зависимость [1]
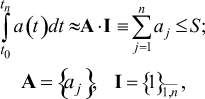(1)
где aj - некоторое осредненное на j-м этапе значение, задаваемое, для определенности, величиной aj = a(tj).
Введем в рассмотрение удельную вектор-функцию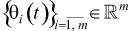 
, каждая компонента которой отражает весовую значимость соответствующей составляющей вектора целей (связанной, например, с доходностью, издержками или уровнем экологичности и т.п.)
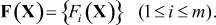(2)
Тогда осредненные за рассматриваемый период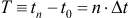 
интегральные взвешенные значения этапных компонент вектора целей (2) можно определить как [2]
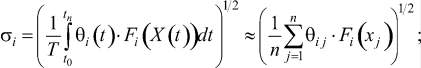
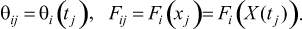
С учётом введенной выше формализации, математическая постановка задачи многокритериальной условной оптимизации, рассматриваемая без сужения общности как минимизация осредненного вектора целей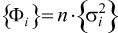 
[3], принимает вид:
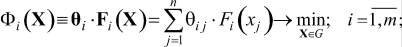(3)
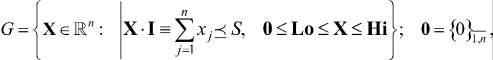(4)
где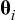
- вектор-строка матрицы весов 
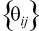, X - вектор переменных модели с интервальными ресурсными ограничениями Lo < Hi, причем
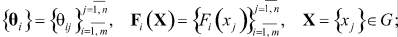(5)
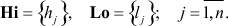
Для области допустимых решений G первое ограничение в (4) определяет отношение порядка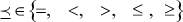 
, обусловливающее взаимосвязь между валовым планом выпуска продукции и максимальным объемом производства S.
Пусть условия ограничений (4) совместны, а каждая i-я скалярная задача (3), (4) разрешима и ее оптимум реализуется в точке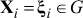 
, где в общем случае 
, 
:
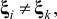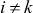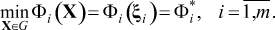(6)
На основе принципа синтеза критериев сведем исходную задачу (3), (4) к однокритериальной условной оптимизации.
Для этого в произвольной точке области допустимых решений X ∈ G определим вектор невязок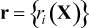 
, с компонентами ri, отражающими неоптимальность реализации каждого скалярного критерия (3) в этой точке, как
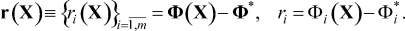(7)
В этом случае общая задача (3), (4) с вектором целей в интерпретации наилучшего компромисса между его отдельными скалярными составляющими критериями как минимума суммы их взвешенных относительных отклонений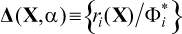 
от своих локальных оптимумов 
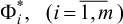с учетом вектора весов 
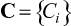может быть представлена как однокритериальная со скалярной функцией цели 
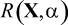в виде:
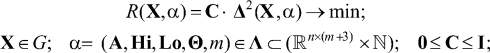(8)
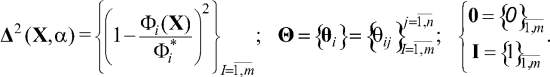
Таким образом, исходная многокритериальная задача (3) с ограничениями (4), определяющими область допустимых решений G, при условии выполнения соотношения баланса (1) сведена к однокритериальной задаче условной параметрической (с вектором параметров α) оптимизации (8), (4). На основе алгоритмизации методов математического программирования разработанная модель реализована в рамках подсистемы ИС оптимального планирования бизнес-процессов с ориентацией на приложение в перерабатывающих отраслях.
Работа поддержана целевой комплексной программой «Научные и научно-педагогические кадры инновационной России».
Список литературы
- Золотарев А.А. Оптимизация издержек конвейерного процесса литейного производства / А.А. Золотарев, Д.О. Дидковский // Системный анализ, управление и обработка информации: сборник научных статей. - Ростов-н/Д.: ДГТУ, Таганрог: ТТИ ЮФУ, 2007. - С. 44-54.
- Золотарев А.А. Оптимизация издержек конвейерного процесса / А.А. Золотарев, Д.О. Дидковский, Ю.Н. Макаров // Инновационные процессы пьезоэлектрического приборостроения и нанотехнологий: сборник трудов VI Международной научно-технической конф. (Анапа, 23‒25 сент. 2008г.) - Ростов-н/Д/, 2008. - С. 269-279.
- Золотарев А.А., Дидковский Д.О. Оптимальная параметризация в задачах распределения ресурсов // Вестник ДГТУ. - 2009. - Т.9, Ч. 2. - С. 5-11.
- Золотарев А.А. Векторная оптимизация распределительных процессов в региональных моделях переработки сырьевых ресурсов // Прикладная и промышленная математика: материалы XI Всерос. Симпозиума. Весенняя сессия (Кисловодск, 1 - 8 мая 2010 г.) [Электронный ресурс]. - Режим доступа: http://www.tvp.ru/conferen/vsppm11/kidag316.pdf (дата обращения: 27.10.2010).
Рецензент ‒
Земляков В.Л., д.т.н., зам. декана факультета высоких технологий Южного федерального университета, зав. кафедрой информационных и измерительных систем ЮФУ, Ростов-на-Дону.