При построении моделей и организации процесса автоматической настройки параметров системы управления необходимым является оценка их влияния на качество переходного процесса. В частных решениях этой задачи предполагается, что все исследуемые параметры могут меняться независимо друг от друга. Однако по мере усложнения систем следует учитывать, что такими свойствами обладают далеко не все параметры. Поэтому одновременная настройка всех варьируемых параметров системы становится затруднительной, что не позволяет говорить о ее действительно оптимальной настройке. Особенно затруднительным становится этот процесс, когда среди варьируемых параметров системы имеются малоинерционные и существенно инерционные либо неуправляемые параметры, при этом некоторые из них взаимосвязаны. Например, при определении модели технологического процесса безынерционные параметры - это расход и давление, а инерционный параметр - температура [2]; при построении моделей показателей качества электроэнергетических систем независимыми параметрами являются только параметры статической нагрузки, а параметры генераторов и асинхронных двигателей, которые приведены в формулярах и технических условиях, коррелированы между собой [3]. Другим примером могут быть нейросетевые системы прогнозирующего управления, в которых число нейронов в скрытом слое (Nc) является безынерционным параметром настройки, а число циклов обучения (Nц) и горизонт прогноза (Nп) относятся к инерционным [5].
Указанный характер варьируемых параметров системы приводит к тому, что если малоинерционные параметры строго выдерживать согласно намеченной ортогональной матрице планирования, а инерционные параметры не обязательно строго выдерживать (так как это дополнительные затраты времени), то получается, что часть матрицы исходных данных, включающая малоинерционные параметры, ортогональна, а другая часть матрицы, включающая инерционные параметры, неортогональна. Вследствие этого при обработке данных проведенного активно-пассивного эксперимента (АПЭ) с использованием методов регрессионного анализа коэффициенты полученного уравнения регрессии оказываются корреляционно связанными между собой. Этого можно избежать, если соблюдается условие ортогональности матрицы независимых переменных [1].
Предположим, что искомая зависимость является линейной вида:
Y = Z0 + b1Z1 + ... + bpZp + bp+1 Zp+1 + ... + bmZm + bm+1 Zm+1 + ... + bnZn.
Тогда соответствующую систему уравнений можно записать в виде
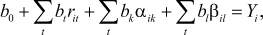 (1)
(1)
где i = 1, ..., N; t = 1,..., p; k = p + 1,...,m; l = m + 1,...,n; rit= ± 1.
В матрице системы (1) столбцы, соответствующие малоинерционным параметрам, т. е. столбцы с t = 1, ..., p, - ортогональные, остальные же столбцы с p + 1 по n - неортогональные. Данную систему уравнений (1) для определения коэффициентов регрессии, независимо друг от друга, можно решить, например, методом ортогонализации столбцов [2], т. е. столбцы, начиная с p + 1 по n, надо доортогонализировать. В случае когда матрица полностью ортогональна, причем уровни варьирования параметров равны ±1, выражение для определения коэффициентов уравнения регрессии сводится к виду
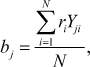
где rij - уровни варьирования параметров, равные ±1; Yi - значение выходного параметра в i-м опыте; N - количество опытов, равное либо полному факторному эксперименту (ПФЭ), либо регулярной реплике от ПФЭ.
Для искусственной ортогонализации столбцов инерционных управляемых и неуправляемых переменных сделаем к ним добавки соответственно Δαik и Δβil таким образом, чтобы сумма (αik + Δαik) и (βil + Δβil) равнялись +1 или -1 в зависимости от того, какие уровни стоят в столбцах ортогональной матрицы планирования (выбранные, например из [4]), к которой сводится исходная матрица. Для того чтобы система (1) не нарушилась, необходимо к правой ее части прибавить соответствующие добавки 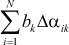 и
и 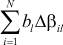 . Тогда система (1) примет вид:
. Тогда система (1) примет вид:
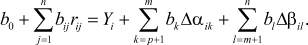 (2)
(2)
Матрица, соответствующая левой части системы (2), является полностью ортогональной, поэтому для решения системы можно использовать формулу:
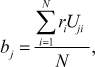 (3)
(3)
где Ui есть соответственно вся правая часть (2).
В результате получаем систему уравнений относительно неизвестных bp+1 ,..., bn :
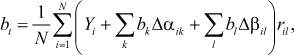
где t = p + 1, ..., n.
Полученная система (4) всегда совместна, так как в матрице системы (2) столбцы ортогональны и, следовательно, линейно независимы. Определив из (4) коэффициенты bp+1 ,..., bn и подставив их в правую часть (2), найдем далее коэффициенты b0, b1, ..., bp по формуле (3).
Таким образом, для построении моделей процессов и систем при наличии переменных с различной динамикой, обусловливающих неортогональность отдельных столбцов матрицы проводимого эксперимента, целесообразно использовать планирование эксперимента. При наличии в составе исследуемых факторов инерционных либо неуправляемых параметров за счет дополнительной ортогонализации столбцов обеспечиваются с помощью метода ортогонализации получение уравнений регрессии и возможность производить независимые оценки отдельным коэффициентам этих уравнений.
Рассмотрим применение изложенной методики для оценки влияния количества нейронов в скрытом слое (Nc), количество циклов обучения (Nц) и величины интервала прогноза (Nп) на показатели качества переходного процесса в системе управления - величину перерегулирования (σ) и степень демпфирования (ξ).
Исходная матрица планирования проведенного активно-пассивного эксперимента с одной управляемой (Nc) и двумя неуправляемыми переменными (Nц, Nп ) имеет вид, представленный в табл. 1. Предположим, что зависимость между факторами x1, x2, x3 (Nc, Nц, Nп) и показателем качества переходного процесса у (перерегулированием) в данной нейросетевой системе управления может быть представлена в виде, линейном относительно искомых коэффициентов b0, b1, b2, b3:
у = b0 + b1x1 + b2x2 + b3x3, (5)
где b0, b1, b2, b3 - коэффициенты регрессии.
Таблица 1
Исходная матрица планирования проведенного АПЭ с одной управляемой (х1)
и двумя неуправляемыми (х1, х2) факторами для оценки перерегулирования
|
Номер опыта |
Уровень фактора xi |
y |
||
|
x1 |
x2 |
x3 |
||
|
1 |
4 |
20 |
10 |
7,2 |
|
2 |
11 |
30 |
14 |
1,2 |
|
3 |
4 |
40 |
5 |
26,6 |
|
4 |
11 |
50 |
15 |
16,5 |
|
5 |
4 |
20 |
16 |
3,0 |
|
6 |
11 |
40 |
20 |
5,0 |
|
7 |
4 |
30 |
5 |
18,7 |
|
8 |
11 |
30 |
25 |
0 |
|
|
|
|
|
|
|
λ1 = 3,5 |
λ2 = 8,1 |
λ3 = 4,4 |
||
Пользуясь методом, описанным выше, найдем линейную модель. Преобразованная матрица, элементы которой находились по формуле , примет вид, представленный в табл. 2.
Таблица 2
Преобразованная матрица планирования АПЭ
|
№ п/п |
Z1 |
Z2 |
Z3 |
y |
|
1 |
-1 |
-1,543 |
-0,857 |
7,2 |
|
2 |
+1 |
- 0,309 |
0,057 |
1,2 |
|
3 |
-1 |
0,926 |
-1,988 |
26,6 |
|
4 |
+1 |
2,160 |
0,286 |
16,5 |
|
5 |
-1 |
-1,543 |
0,514 |
3,0 |
|
6 |
+1 |
0,926 |
1,429 |
5,0 |
|
7 |
-1 |
-0,309 |
-1,988 |
18,7 |
|
8 |
+1 |
-0,309 |
2,557 |
0 |
Таблица 3
Ортогональная матрица планирования АПЭ
|
№ п/п |
Z1 |
Z2 |
Z3 |
U |
|
1 |
-1 |
-1 |
-1 |
7,2 + 0,543b2 - 0,143b3 |
|
2 |
+1 |
-1 |
-1 |
1,2 - 0,691b2 - 1,057b3 |
|
3 |
-1 |
+1 |
-1 |
26,6 + 0,074b2 + 0,988b3 |
|
4 |
+1 |
+1 |
-1 |
16,5 - 1,160b2 - 1,286b3 |
|
5 |
-1 |
-1 |
+1 |
3,0 + 0,543b2 + 0,486b3 |
|
6 |
+1 |
-1 |
+1 |
5,0 - 1,926b2 - 0,429b3 |
|
7 |
-1 |
+1 |
+1 |
18,7 + 1,309b2 + 0,988b3 |
|
8 |
+1 |
+1 |
+1 |
0 + 1,309b2 - 1,557b3 |
Выбрав ортогональную матрицу и сведя к ней предыдущую, сделав к неуправляемым переменным те или иные добавки, получим ортогональную матрицу, представленную в табл. 3.
По формуле (3) находим:
b1 = 1/8(- 32,6 - 4,937b2 - 6,958b3); b2 = 1/8(45,6 + 3,06b2 + 0,276b3);
b3 = 1/8(-24,6 + 2,469b2 + 0,986b3); b3 = - 0,2652;
b2 = 9,2378; b1 = - 9,9951; b0 = 9,775.
Используя вычисленные коэффициенты b0, b1, b2 и b3, получим следующее уравнение:
Z = 9,775 - 9,9951Z1 + 9,2378Z2 - 0,2652Z3.
Выполнив обратное преобразование, получим искомое уравнение регрессии:
у = 9,775 - 9,9951(x1 -7,5)/3,5 + 9,2378(x2 - 32,5)/8,1- 0,2652(x3 -13,75)/4,4
или в окончательном виде
y = - 5,045 - 2,8557x1 + 1,14x2 - 0,0603x3. (6)
Аналогично получено уравнение связи между факторами x1, x2, x3 (Nc, Nц, Nп) и показателем качества переходного процесса - степенью демпфирования (ξ) в нейросетевой системе управления в виде:
ξ = - 0,4837 + 0,0725x1 - 0,0177x2 + 0,0171x3. (7)
Для построения зависимости (7) исходная матрица планирования проведенного АПЭ приведена в табл. 4.
Поскольку расчетные значения перерегулирования и степени демпфирования соответствуют заданным требованиям к переходному процессу, то полученные уравнения линейного приближения можно считать информативными. В результате можно отметить, что увеличение числа нейронов в скрытом слое приводит к уменьшению перерегулирования σ (коэффициент b1 < 0 в уравнении (6)), и увеличению демпфирования ξ (коэффициент b1 > 0 в уравнении (7)). Например, при Nc = 9, Nц = 50 и Nп = 15 расчетные значения σ и ξ равны σ = 25,4 %, ξ = 0,5077; при Nc = 11, Nц = 50 и Nп = 15 расчетные значения σ и ξ равны σ = 19,9 %, ξ = 0,6527. При других значениях Nц = 30 и Nп = 14 и при тех же значениях Nc = 9 и Nc = 11 получаем σ = 2,8 %, ξ = 0,8446 и σ = -2,6 %, ξ = 0,9896. При постоянных значениях Nc = 11 и Nп = 14, изменяя Nц от 40 до 30, получаем уменьшение перерегулирования σ от 8,7 до -2,6 % с изменением характера переходного процесса от апериодического до монотонного.
Таблица 4
Исходная матрица планирования проведенного АПЭ с одной управляемой (х1)
и двумя неуправляемыми (х1, х2) факторами для оценки степени демпфирования ξ
|
Номер опыта |
Уровень фактора xi |
ξ |
||
|
х1 |
x2 |
x3 |
||
|
1 |
4 |
20 |
10 |
0,45 |
|
2 |
11 |
30 |
14 |
0,68 |
|
3 |
4 |
40 |
5 |
0,19 |
|
4 |
11 |
50 |
15 |
1,0 |
|
5 |
4 |
20 |
16 |
1,0 |
|
6 |
11 |
40 |
20 |
1,0 |
|
7 |
4 |
30 |
5 |
0,19 |
|
8 |
11 |
30 |
25 |
1,0 |
|
|
|
|
|
|
|
λ1 = 3,5 |
λ2 = 8,1 |
λ3 = 4,4 |
||
Таким образом, в случае не полностью ортогональной матрицы планирования эксперимента, обусловленной наличием среди исследуемых факторов неуправляемых либо инерционных параметров, использованная методика обработки данных обеспечивает получение нейросетеых моделей и возможность производить независимые оценки отдельным коэффициентам этих моделей.
Список литературы
- Адлер Ю.П. Планирование эксперимента при поиске оптимальных условий / Ю.П. Адлер, Е.В. Маркова, Ю.В. Грановский. - М.: Наука, 1976. - 279 с.
- Бабаянц А.В. Об обработке данных активно-пассивного эксперимента / А.В. Бабаянц, И.А. Мамулов // Автоматизация микробиологических производств (Сборник работ, вып. II ). - Грозный: НИПИнефтехимавтомат, 1976. - С. 85-93.
- Зубарев Ю.Я. Планирование вычислительного эксперимента в электроэнергетике / Ю.Я. Зубарев [и др.]. - СПб.: Энергоатомиздат, 2000. - 328 с.
- Лубенцов В.Ф. Практический математико-статистический анализ биотехнологических систем. - Ставрополь: Изд-во СевКавГТУ, 2000. - 111 с.
- Ноткин Б.С. Эффективная нейросетевая идентификация инверсной динамики объекта управления для синтеза прогнозирующих систем управления / Б.С. Ноткин, К.В. Змеу //
Идентификация систем и задачи управления: труды IV Международной конференции (SICPRO 05), Москва 25‒28 января 2005 г. - М.: ИПУ РАН, 2005. - С. 887-900.
Рецензенты:
Лубенцов В.Ф., д.т.н., профессор кафедры «Информационные системы, электропривод и автоматика» Невинномысский технологический институт (филиал) ГОУ ВПО «Северо-Кавказский государственный технический университет», Невинномысск;
Мочалов В.П., д.т.н., профессор, зав. кафедрой «Автоматизированные системы обработки информации и управления» ГОУ ВПО «Северо-Кавказский государственный технический университет», Ставрополь.




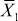 = 7,5
= 7,5
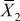 = 32,5
= 32,5
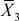 = 13,75
= 13,75
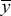 = 9,775
= 9,775