Вводная часть. При разработке моделей сложных пространственно-распределенных социоприродоэкономических систем (СПЭС) [6] возникает задача формирования адекватной структуры математической модели. Проблема моделирования и управления такими объектами связана как с распределенностью системы, так и с наличием нелинейных связей между подсистемами. Обеспечение эффективного взаимодействия предприятий с внешней и окружающей природной средами требует масштабного развития транспортной инфраструктуры и рационального управления грузопотоками. Поэтому особое значение приобретают методы расчета и оптимизации транспортных систем (ТС). Возрастает важность корректного применения методов расчета.
Несмотря на многочисленность предложенных моделей оптимизации, высокую научную и практическую значимость работ по данной проблеме, еще имеется ряд возможностей по совершенствованию организации, планирования и управления транспортными потоками.
Отличительными особенностями автотранспортных систем являются:
1. Транспортная система представляет собой распыленную дискретную систему, состоящую из целого множества элементов, определяющих сложность ее структуры и/или поведения: погрузочно-разгрузочные пункты; транспортные средства; предприятия, осуществляющие грузовые и/или пассажирские перевозки; транспортная сеть; грузовой склад (терминал), логистические центры и т.п.; пассажирские вокзалы (станции, остановки и т.п.); перевозочный (транспортный) процесс; поток транспортных средств и др. Такая система с течением времени меняет свое состояние, последовательно переходя из состояния S0 в состояние Sn.
2. Процессы в транспортных сетях можно рассматривать как случайные события, ход и исход которых зависит от многих причин случайного характера. Переход системы из одного состояния в другое происходит «скачком», а так как каждую ездку, рейс можно перечислить (пронумеровать), то транспортный процесс является процессом с дискретным состоянием.
3. Ежесменно (ежесуточно) такая система приходит в первоначальное состояние S0. Этот переход может осуществляться с любого состояния Si. Следовательно, транспортный процесс, происходящий в автотранспортных системах, является также циклическим случайным процессом с дискретным состоянием.
4. Принятым практикой является использование коэффициентов 0 и 1 при поставках хij в связи c предположением об отсутствии потерь.
5. При невыполнении условия баланса поставки вводится дополнительный узел (отправитель или получатель), которого называют фиктивным.
Если у отправителя груза больше, чем требуется потребителю, то вводится фиктивный узел - грузополучатель, для которого объем завоза груза составит
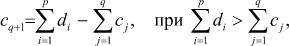(1)
где p - количество пунктов производства; q - количество пунктов назначения; di - фиксированный ресурс груза в пункте производства (i = 1, ..., p); сj - объем потребления груза в пункте назначения (j = 1, ...,q).
Если спрос превышает предложение, то вводится фиктивный узел - грузоотправитель, для которого объем вывоза составит
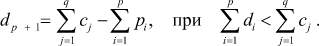(2)
Фиктивный потребитель может являться складом, куда поступает нереализованная продукция, или реальным потребителем, получившим дисконт (скидку) на стоимость продукции, которая превышает спрос.
6. В качестве теоретических основ для моделирования перечисленных объектов применяются чаще всего аппараты теории линейного (нелинейного, динамического) программирования, массового обслуживания, управления запасами, игр и т.д. При этом делаются предположения либо о полностью детерминированном функционировании систем (например, в случае решения разнообразных транспортных задач линейного программирования), либо о вероятностном характере происходящих процессов (в большинстве других случаев).
В статье [1] рассмотрен подход, позволяющий ставить и решать задачи моделирования ТС на макроскопическом уровне, когда представление ТС допускает абстрагирование от описания отдельных элементов. Основной задачей при этом является характеристика поведения системы в целом и анализ особых состояний ТС. В основе описания модели используются положения нелинейной динамики, в рамках которой рассматриваются неравновесные состояния систем. Подход, который используется в теории макросистем, позволяет расширить указанные рамки и допускает детерминированное поведение систем, состоящих из элементов со стохастическим типом поведения. Предложенная модель грузового склада [1] позволяет осуществлять планирование перевозок только из одного распределительного центра.
Автор [1] отмечает, что построенные модели, конечно, не следует считать единственным вариантом рассматриваемых систем, так как набор причинно-следственных связей, описывающих «поведение» участников транспортных процессов, может быть различным. В работе [1] сформулированы проблемы для дальнейшего исследования. Часть из них решается в данной работе:
1) идентификация моделей систем и определение коэффициентов, соответствующих реальным условиям;
2) уменьшение числа параметров в уравнениях до минимально возможного с целью снижения размерности пространства параметров;
3) выявление объектов управления в моделях, постановка и решение задач оптимального управления в соответствии с принятыми критериями.
Ниже рассматривается задача о завозе-вывозе грузов одновременно из нескольких дистрибьюторских центров. Свой метод решения подобной задачи предложил профессор Палагин Ю.И. [7]. Такая задача возникает в тех случаях, когда торговая компания, поставляющая товары своим клиентам, имеет единый центр приема и обработки заказов, который осуществляет планирование доставки и распределяет заказы по исполняющим их распределительным центрам или складам отгрузки.
На наш взгляд, перспективным направлением в моделировании сложных автотранспортных систем являются окрестностные модели. В работах [2‒5] введены и исследованы окрестностные модели, развивающие общие подходы теории систем и являющиеся обобщением для традиционных дискретных моделей таких, как конечные автоматы, клеточные автоматы, транспортные модели и т.д. В вопросе улучшения функционирования системы актуальным является изучение связи значений показателя качества работы системы с окрестностной структурой. Поэтому предложены подходы по оптимизации в данном контексте структуры окрестностей.
Приведем обобщенное определение окрестностных моделей и покажем место транспортных сетей в классе окрестностных моделей.
1. Определение окрестностной модели
Окрестностная модель в общем случае описывается набором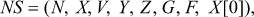 
где:
1) 
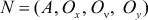- структура окрестностной модели, 
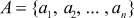- множество узлов, Ox - окрестности связей узлов по состояниям, Ov - окрестности связей узлов по управлениям, Oy - окрестности связей узлов по выходным воздействиям. Для каждого узла 
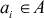определена своя окрестность по состояниям 
,
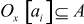управлениям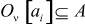 
и выходам 
; 
.
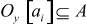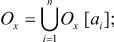
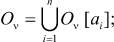
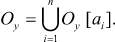2) X ∈ Rn - вектор состояний окрестностной модели в текущий момент времени;
3) V ∈ Rm - вектор управлений окрестностной модели в текущий момент времени;
4) Y ∈ Rl - вектор выходов окрестностной модели в текущий момент времени;
5) 
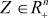‒ вектор временных задержек в узлах,
где R+ - множество неотрицательных действительных чисел;
6) 
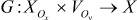- функция пересчета состояний окрестностной модели (в общем случае недетерминированная), где 
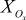- множество состояний узлов, входящих в окрестность Ox; 
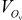- множество управлений узлов, входящих в окрестность Ov;
7) 
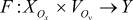- функция пересчета выходов окрестностной модели (в общем случае недетерминированная);
8) X[0] - начальное состояние модели.
В частных случаях для различных дискретных моделей отдельные составляющие окрестностной модели могут отсутствовать.
Функции G и F могут быть произвольными, например линейными, билинейными, квадратичными, полиномиальными и т.д. В линейном случае G и F можно представить в виде системы линейных уравнений:
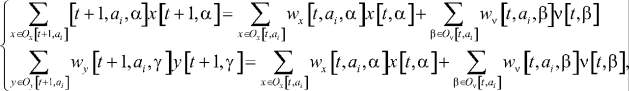(3)
где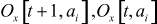 
- окрестности узла ai по x соответственно в моменты времени t + 1 и t, Ov[t, ai] - окрестность узла ai по v в момент времени t, Oy[t + 1, ai] - окрестность узла ai по y в момент времени t + 1, , 
, 
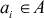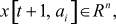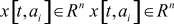- состояния в узле ai модели соответственно в моменты времени t + 1 и t, 
-
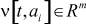вход в узле ai модели в момент времени t,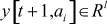 
- выход в узле ai модели в момент времени t + 1, 
, 
, 
, 
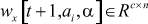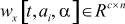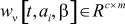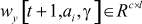- матрицы-параметры, a, β, γ ∈A.
Представим модель (3) в матричном виде. Для этого определим матрицы Wx[t + 1], Wx[t] коэффициентов по состояниям в моменты времени t + 1 и t соответственно, матрицу Wv[t] коэффициентов по входам в момент времени t, матрицу Wy[t + 1] коэффициентов по выходам в момент времени t + 1:
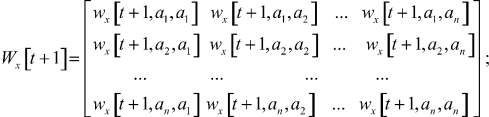
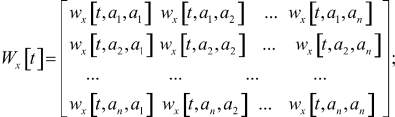
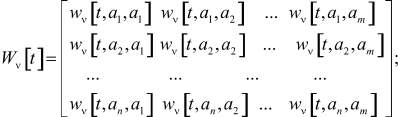
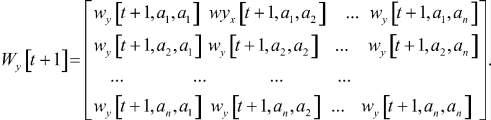
Тогда модель (3) будет иметь вид:
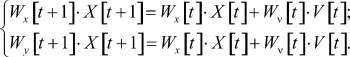(4)
В случае, когда функции W и F являются нелинейными, модель (4) преобразуется к виду:
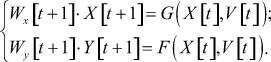(5)
Изменяя составляющие общего описания окрестностной модели, можно получить различные классы дискретных распределенных моделей. Схема связи классов дискретных моделей представлена на рис. 1.
Окрестностные модели можно разделить на детерминированные и недетерминированные. В свою очередь, недетерминированные окрестностные модели делятся на четкие и нечеткие. Связи между узлами могут быть многомерными: стоимость перевозок различными видами транспорта, категория дороги, маршрут доставки, в перевозке может быть задействовано несколько видов транспорта (железнодорожный, автомобильный транспорт). Транспортные сети могут быть четкими или нечеткими; четкие по одним переменным и нечеткие по другим переменным. Нечеткость выражена по окрестностям, по значениям. Транспортные сети делят на детерминированные и недетерминированные.
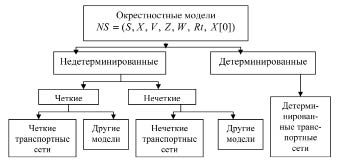
Рис. 1. Схема связи классов дискретных моделей
2. Транспортные сети как частный случай окрестностной модели
Прежде всего, покажем, что дискретные модели, в частности транспортные модели, являются разновидностями окрестностных систем с некоторыми вариациями, и важную роль играет матрица инциденций, отражающая связи между узлами системы.
Структура транспортной системы напоминает структуру нейронной сети с двумя слоями без скрытого слоя: входным и выходным без входного и выходного сигналов. Особенность транспортной системы с точки зрения окрестностного подхода состоит в независимом (в общем случае, одновременном) срабатывании всех окрестностей, описывающих связи узлов поставщиков с узлами потребителями.
Транспортная сеть представляет собой направленный (ориентированный) граф. Модель транспортной сети представляют в виде графа (рис. 2). В графе введена окрестностная структура. Формулировка модели: имеется N= p+ q узлов (см. рис. 2); p пунктов производства с фиксированными ресурсами груза di (i =1, ..., p); q пунктов назначения с заданными объемами потребления данного груза сj (j=1, ...,q); при этом предполагается, что суммарный спрос равен суммарному предложению.
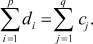(6)
Все пункты связаны транспортной сетью, и для каждой транспортной коммуникации известны удельные показатели эффективности её использования Сij. Требуется организовать систему перевозок, обеспечивающую полное удовлетворение потребностей с наибольшим эффектом.
Рассмотрим алгоритмы решения транспортной задачи с использованием симметричной окрестностной модели
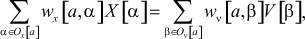(7)
где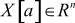 
, 
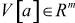-состояние, вход и выход в узле системы; 
, 
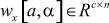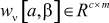- матрицы-параметры; Ox[a], Ov[a] - окрестность узла a по состоянию и входному воздействию соответственно; a, α, β∈A, 
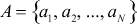- конечное множество значений дискретного аргумента системы, |A| = N.
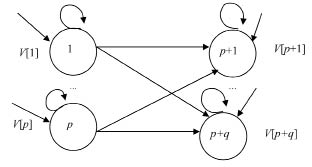
Рис. 2. Схема окрестностной модели из N= p+q узлов
Количество узлов в транспортной задаче при окрестностном подходе равно N = p + q, где p - количество пунктов поставки (производства), а q - количество пунктов потребления (суммирование в (7) по всем N узлам). Структура транспортной системы определена окрестностями Ox[a], Ov[a] и соответствующими матрицами инциденций Rx, Rv, единица (ноль) в которых на месте (i, j) означает наличие (отсутствие) связи i-го узла с j-м по состоянию (входу).
Значения коэффициентов модели wx[a, α] представляют собой связи между узлами по состоянию и в терминах теории транспортных систем могут быть рассмотрены при соответствующем задании векторов X[a], V[a] и матрицы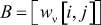 
(в общем случае
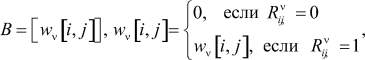
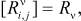
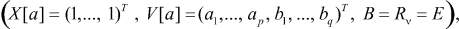
как перевозки из пунктов производства в пункты потребления, т.е.
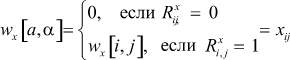
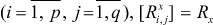
и матрица перевозок совпадает с матрицей связей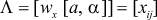 
(при добавочном условии xij = xji).
Таким образом, если уравнение (7) в соответствии с [4, с. 9] представить в матричной форме
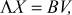(8)
то транспортная модель в окрестностном виде задается набором
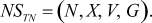
Смена окрестностей (связей поставщиков с потребителями и потребителей с поставщиками) соответствует появлению новой программы перевозок (учёту новых маршрутов поставок). Смене окрестностей соответствует преобразование матрицы инциденций.
Заключение
В работе показано, что транспортные сети в терминах введённого определения являются разновидностями окрестностных систем. Окрестностные модели транспортных сетей отличаются следующими характеристиками: наличием состояний, входов и отсутствием выходных воздействий. В работе рассмотрены предложения по оптимизации в данном контексте структуры окрестностей, показано, что важную роль играет матрица инциденций, отражающая связи между узлами системы.
На основе методологии использования окрестностных моделей для расчета и оптимизации транспортных потоков, принципов автоматизации построения моделей и принципов информационного обеспечения моделей решена научно-техническая проблема автоматизации расчета и оптимизации функционирования транспортных систем, имеющая важное народнохозяйственное значение.
Разработанные алгоритм и процедуры решения задачи не требуют большого объема памяти и вычислений и дают возможность планировать рациональную доставку грузов с любым количеством заказчиков, что отличает рассмотренный подход от [7]. Выполненные исследования и разработанные подходы формируют качественно новый уровень научных основ для оценки проектных решений по развитию транспортных узлов, оптимизации технологических процессов грузодвижения на территории региона.
Показателем эффективности предлагаемой задачи оптимизации является повышение синергетического эффекта для участников цепи поставок. Этот эффект оценивается возможностью получения максимальной прибыли от реализации продукции за счет рационального управления транспортными потоками и высокого уровня взаимодействия между участниками системы.
Список литературы
-
Агуреев И.Е. Нелинейные модели транспортных систем // Мир транспорта и технологических машин. - Орел:ГТУ, 2009. - №2 - С. 3‒16.
-
Блюмин С.Л., Шмырин A.M. Окрестностные системы. - Липецк: ЛЭГИ, 2005. - 132 с.
-
Окрестностное моделирование сетей Петри / С.Л. Блюмин, А.М. Шмырин, И.А. Седых, В.Ю. Филоненко. - Липецк: ЛЭГИ, 2010. - 124 с.
-
Блюмин С.Л., Шмырин А.М., Шмырина О.А.. Билинейные окрестностные системы. - Липецк: ЛГТУ, 2006. - 130 с.
-
Карабутов Н.Н., Шмырин А.М. Окрестностные системы: Идентификация и оценка состояния. - Липецк: ЛГТУ, 2005. - 132 с.
-
Корчагин В.А. Социоприродоэкономические автотранспортные системы // Грузовое и пассажирское хозяйство. - 2008. - №6. - С. 12-16.
-
Палагин Ю.И. Оптимальное планирование задач завоза и вывоза грузов из нескольких распределительных центров // Транспорт: наука, техника, управление / ВИНИТИ. - 2010. - № 2. - С. 12-15.
Рецензенты:
Баженов С.П., д.т.н., профессор, зав. кафедрой «Автомобили и тракторы» ГОУ ВПО «Липецкий государственный технический университет», Липецк;
Московцев В.В., д.э.н., профессор, декан экономического факультета НОУ ВПО «Липецкий эколого-гуманитарный институт», Липецк.