В настоящее время успешно развивается теория принятия решения (ТПР) как часть теории систем искусственного интеллекта, изучающая общие условия, подходы и закономерности в различных предметных областях при исследовании задач принятия решения (ЗПР) [1].
Другой успешно развивающейся областью в настоящее время являются информационные технические системы (ИТС), которые проникают во все сферы деятельности человека. Особенностью современных ИТС является решение задач, которые в недавнем прошлом решались только с помощью интеллекта человека. В работе рассмотрены вопросы применения ЗПР в области выбора цифровых средств реализации алгоритмов обработки информации при проектировании ИТС. К настоящему времени накоплен богатый опыт в методах и средствах реализации алгоритмов цифровой обработки информации (ЦОИ) [2]. Однако выбор этих средств реализации алгоритмов при проектировании ИТС является в большей степени субъективным, при этом невозможно оценить ‒ насколько оптимальным явилось выбранное средство. В этой связи актуальной является задача разработки СППР, реализующей методы объективного выбора средства реализации алгоритмов работы ИТС.
Целью данной работы является применение теории принятия решений для разработки метода объективного выбора цифрового средства реализации алгоритма работы проектируемой информационной технической системы последовательной обработки данных. При этом метод выбора работает с альтернативными вариантами устройств ЦОИ ‒ универсальные ЭВМ с использованием программных средств, микроконтроллеры или программируемые логические интегральные схемы (ПЛИС).
1. Обобщенная структура формирования решения
Основным направлением теории принятия решений является отыскание оптимального решения, которое максимизирует (или минимизирует) целевую функцию, моделирующую степень предпочтительности при принятии решения (рис. 1). Предпочтительность того или иного исхода оценивают величиной специальной числовой функции, значения которой принимаются за тот или иной критерий. Оптимальным считается такой вариант проведения операции, который обеспечивает наилучшее значение критерия или сочетание значений нескольких критериев.
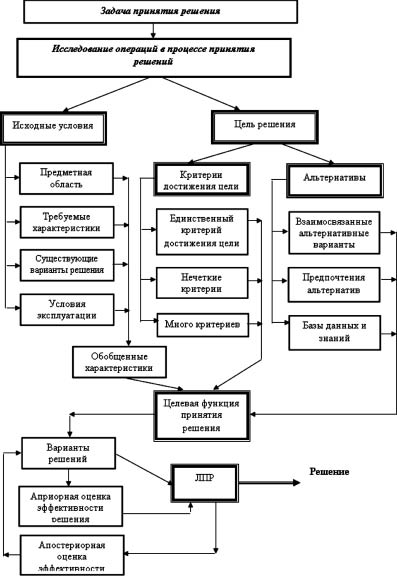
Рис. 1. Структура взаимодействия условий в задаче принятия решения
Ключевым элементом в ЗПР является целевая функция (ЦФ) принятия решения, которая представляет собой математическую модель, в количественном виде объединяющую исходные условия, критерии достижения цели и совокупность альтернатив формируемых решений. Полученные варианты решений оцениваются лицом, принимающим решение (ЛПР), формируя апостериорную оценку эффективности. Кроме того, для полученных вариантов решений может быть оценена эффективность варианта априори. Конечное решение принимает ЛПР, то есть человек, наделенный соответствующими полномочиями и несущий ответственность.
В настоящее время СППР успешно развиваются в области экономики и управления [1]. Применение подходов, используемых в СППР, для решения технических задач развиты слабо. В работе предлагается развить положения ТПР в СППР в области оптимального проектирования специализированных цифровых устройств обработки сигналов, когда требуется реализовать объективный выбор средства реализации ИТС. Это является одним из важных вопросов, решение которого определяет основные взаимосвязанные показатели качества проектируемой ИТС, такие, как быстродействие, надежность, помехоустойчивость, габариты, масса и потребляемая мощность.
2. Общий подход к разработке метода выбора средства реализации алгоритмов
Развитие технологий интегральных схем привело к разнообразию средств реализации алгоритмов ЦОИ, среди которых можно выделить такие, как программные на базе универсальных ЭВМ, микроконтроллерные и средства на базе ПЛИС. Все эти средства ЦОИ в настоящее время являются конкурентами. При разработке метода объективного выбора варианта реализации ИТС необходимо определить вид алгоритма. Им может быть, например, один из трех: управляющий, вычислительный или преобразовательный.
Последовательность действий в методе объективного выбора цифрового средства реализации ИТС состоит в следующем:
определяется множество основных параметров проектируемой ИТС: {X1, X2, ...Xn }, их единицы измерения и их максимальные значения: {γ1, γ2, ... γn };
выполняется нормирование параметров по максимальным значениям для приведения их к безразмерному виду;
формируется обобщенная характеристика как функция частных параметров, которая дает обобщенную характеристику формируемой модели, например, в виде суммы
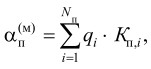
определяются весовые коэффициенты qi, входящие в αп(м), которые назначаются в зависимости от приоритетов коэффициентов параметров Kп,i , исходя из доли влияния каждого параметра на обобщенную характеристику αп(м). Коэффициенты Kп,i определяются при рассмотрении каждого частного параметра с учетом его значимости. Если приоритеты неизвестны, то принимается равномерная значимость параметров;
определяются коэффициенты весомых параметров KВП,i , которые необходимо учитывать отдельно в ЦФ, так как они оказывают существенное влияние на решение задачи. Это может быть коэффициент реального времени KВП,РВ , коэффициент вида алгоритма KВП,ВА и другие;
формируется ЦФ выбора варианта реализации модели ИТС в аналитическом виде, которая определяет поведение модели в зависимости от весомых параметров KВП,i и обобщенной характеристики αп(м) :
;
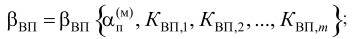для ЦФ выполняется разделение значений на зоны, соответствующие принятым вариантам реализации ИТС. Совокупность зон или интервалов значений функции выбора определяет множество моделей вариантов реализации
ВР(М) = { ВР1 ,ВР2, ....,ВРL, }.
Если неизвестно преобладание какого-либо варианта реализации, то выбирается равномерное разделение области допустимых значений функции выбора на L зон или интервалов. При этом получаем множество интервалов, характеризующих различные варианты реализации ИТС:
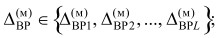
формируется критерий выбора варианта реализации модели ИТС. Попадание значения функции выбора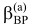 
для конкретных значений обобщенной характеристики αп(м) и весомых параметров KВП,i в соответствующую зону или интервал значений и будет определять вариант реализации ИТС, то есть является решением задачи выбора. Условие попадания в некоторую зону варианта реализации ИТС можно записать в виде: ВР(а) = ВР(м) {ВР1, ВР2, ..., ВРL }, при 
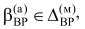, т.е. принимается решение о выборе варианта реализации алгоритма ВР(а), принадлежащего множеству ВР(м) при условии попадания значения функции выбора 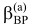интервал значений, соответствующих одной из трех зон функции выбора модели 
.
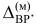Для разработки конкретного метода СППР ограничим предметную область выбором цифрового средства реализации алгоритмов следующими условиями:
1) из всего многообразия ИТС будем рассматривать ИТС с использованием устройств ЦОИ;
2) исходным сигналом для проектируемой ИТС является последовательный временной сигнал S(t), преобразуемый в последовательный поток данных; 3) другим условием является реализация в виде специализированной ИТС, когда проектируется некоторая система с заданными функциями, которые в процессе эксплуатации кардинально не изменяются.
3. Метод выбора цифрового средства реализации алгоритма ЦОИ в ИТС
Рассмотрим модель принятия решения при выборе одного их трех способов реализации алгоритмов: программного на базе универсальной ЭВМ, микроконтроллерного и с использованием ПЛИС. Для конкретизации метода необходимо учесть характеристики обрабатываемого сигнала и алгоритма обработки данных: динамический диапазон входного сигнала DS; скорость потока данных, характеризуемая количеством отсчетов обрабатываемого сигнала в единицу времени ПS; вид преобразования в виде параметра трансформации отсчетов NTO; параметр сложности алгоритма САЛ; количество вычислительных операций NОП; время выполнения операций вычислительного процесса ТВО. После выполнения нормирования проанализированных параметров по множеству характеристических свойств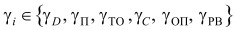 
получено множество безразмерных параметров:
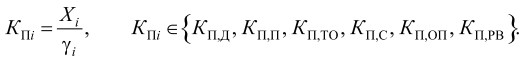
Все множество нормированных параметров в виде коэффициентов (1) необходимо связать некоторой целевой функцией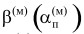 
от обобщенной характеристики αп(м), которая формируется в виде суммы нормированных коэффициентов с использованием весовых коэффициентов:
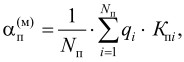
где Nп ‒ число параметров; qi - весовой коэффициент параметра, который определяется исходя из доли влияния данного коэффициента параметра Кп,i на обобщенную характеристику αп(м) модели вычислительного процесса.
Далее в работе обосновываются выражения для коэффициентов параметров Кп,i (1):
1) коэффициент динамического диапазона входных данных:
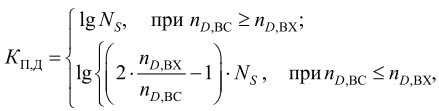
где NS ‒ число уровней квантования входного сигнала, nD,BX ‒ разрядность входного потока данных, nD,BC ‒ разрядность шины даны вычислительной устройства;
2) коэффициент последовательного потока данных:
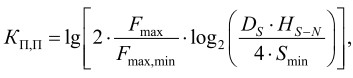
где HS-N ‒ отношение сигнал-шум; Smin ‒ минимальное значение входного сигнала;
3) коэффициент трансформации отсчетов: КП,ТО = lg(1 / NTO) , где NTO = NL,M / NI,J учитывает вид преобразования входных массивов данных в виде отношения количества отсчетов выходного сигнала результата преобразования NL,M к количеству отсчетов входного сигнала NI,J зависит от используемого алгоритма и не связан с технической реализацией преобразования;
4) коэффициент сложности модели алгоритма:
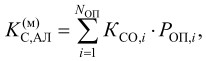
где КСО,i, ‒ коэффициентов сложности операций, NОП,i / NОП = PОП,j i ‒ оценка вероятности появления i-операции;
5) коэффициент реального времени:
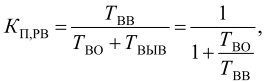
где ТВО ‒ время выполнения операций алгоритма, ТВВ ‒ интервал поступления входных отсчетов, ТВВ = ТВЫВ.
Как было отмечены выше, ядром структуры принятия решения в СППР является целевая функция (ЦФ) (рис. 1), которая включает в себя исходные условия, критерии получаемого решения и возможные варианты решений. При разработке метода выбора цифрового средства реализации алгоритма работы ИТС последовательной обработки данных остановим свой выбор на ЦФ с насыщением, которая является наиболее простой:
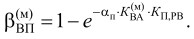
Максимальное значение коэффициента реального времени KП,РВ = 1 , минимальное принято за 0,05. На графиках (рисунок 2) целевой функции моделей алгоритмов отмечены три зоны ‒ области значений целевой функции, соответствующие цифровым средствам реализации: зона 1 ‒ для программных средств реализации (ПР), зона 2 ‒ для микропроцессорных (МП) на базе микроконтроллеров, зона 3 ‒ для программируемой логики (ПЛ) в виде ПЛИС. Получается множество цифровых средств реализации моделей алгоритмов СР(м) = {ПР, МП, ПЛ}.
Выбрано равномерное разделение области допустимых значений целевой функции на 3 зоны, которые характеризуются множеством
,
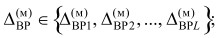где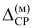 
- интервал средств реализации моделей алгоритмов, причем 0≤ 
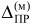< 0,33; 0,33 ≤ 
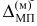< 0,67; 0,67 ≤ 
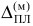≤ 1.
Попадание значения целевой функции для конкретного алгоритма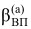 
в соответствующую зону целевой функции модели алгоритма (рис. 2) и определяет средство реализации. Условие попадания в некоторую зону средств реализации можно записать в виде 
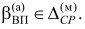В общем виде решение о выборе средства реализации примет вид: СР(а) = СР(м) {ПР, МП, ПЛ}.
Приведем пример, характеризующий совместное влияние как коэффициента реального времени Кп,рв, так и обобщенной характеристики αп(м) на поведение целевой функции. Например, требуется выбрать средство реализации алгоритма по обработке телевизионного сигнала в системе технического зрения. В этом случае требования к параметрам сигнала и алгоритма более высокие. Fmax= 5 МГц, то есть период следования отсчетов ТВВ=100 нс. Время выполнения операций ТВО<100 нc, то есть весь алгоритм обработки должен выполняться в темпе поступлении отсчетов в реальном времени. Высокие требования к параметрам алгоритма и входных сигналов приведут к значению обобщенной характеристики αп(м) > 1, в конечном счете, исходя из целевой функции (рис. 2) получим попадание в зону средств с программируемой логикой. Далее необходимо детализировать поведение обобщенной характеристики в зависимости от входящих в него частных нормированных параметров, определяемых исходя из заданных параметров исходного алгоритма и параметров исходного сигнала. Кроме того, необходимо определить весовые коэффициенты, учитывающие влияние каждого рассмотренного параметра на обобщенную характеристику αп(м). Сделать это удалось после разработки программного обеспечения (ПО) средства, реализующего разработанный метод выбора, и обоснования цифрового средства реализации заданного алгоритма.
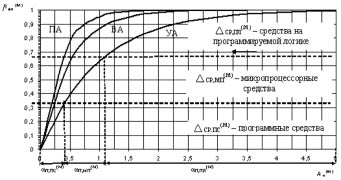
Рис. 2. Целевая функция для выбора цифровых средств реализации алгоритма
Заключение
В работе обобщаются результаты развития теории принятия решений, являющейся основой систем поддержки принятия решений. Рассмотрены структура задач принятия решений, основные этапы, критерии, виды получаемых решений. Сформирована схема последовательности принятия решений, ядром которой является целевая функция, объединяющая исходные условия, цели решения, критерии и альтернативные варианты получаемого решения.
Разработан метод выбора средства реализации исходного алгоритма, основанный на сравнении значения целевой функции для конкретного вычислительного процесса и значения целевой функции соответствующей модели алгоритма. Для модели вычислительного процесса обосновано использование значимых характеристик сигналов и алгоритмов их обработки. Разработанный метод позволяет обоснованно с использованием количественных оценок выбрать базу реализации алгоритма специализированных устройств цифровой обработки в ИТС последовательных потоков данных.
Список литературы
- Черноруцкий И.Г. Методы принятия решений. ‒ СПб.: БХВ-Петербург, 2005.
- Сальников И.И. Растровые пространственно-временные сигналы в системах анализа изображений. ‒ М.: Физматлит, 2009.
- Брукинг А., Джонс П., Кокс Ф. и др. Экспертные системы. Принципы работы и примеры. ‒ М.: Радио и связь, 1987.
Рецензенты:
Светлов Анатолий Васильевич, д.т.н., профессор, зав. кафедрой радиотехники и радиоэлектронных систем Пензенского государственного университета;
Федотов Николай Гаврилович, д.т.н., профессор, зав. кафедрой экономической кибернетики Пензенского государственного университета.