Распределенные информационные системы, построенные на базе вычислительных и телекоммуникационных сетей, занимают в современном мире все более значимое место за счет расширения сферы применения, повышения качества обслуживания пользователей [1-3, 7]. Совершенствование сетевых технологий позволило создавать корпоративные информационные системы и вычислительные сети большой размерности, обслуживающие тысячи пользователей. Развитие этих систем, обслуживающих большое количество пользователей и реализующих большое количество разнообразных прикладных программ, привело к возникновению проблемы [4-6], связанной с прогнозированием уровня нагрузки на сервера приложений.
Коммуникационный сервер системы непрерывного мониторинга состояния сложных технических объектов является ключевым звеном при передаче информации от контролируемых объектов до рабочих мест операторов. Особенностью программной архитектуры коммуникационного сервера является то, что фактически работа модуля взаимодействия с регистраторами не зависит от работы модуля передачи данных. При этом для исследования реакции коммуникационного сервера на входящие потоки данных различной интенсивности достаточно ограничиться использованием схемы, изображенной на рис. 1. Выдача данных регистраторами производится при получении от коммуникационного сервера соответствующей команды в ответ на запрос авторизации. Этот запрос формируется при достижении наличия определенного количества записей во временном хранилище данных. Передача данных со стороны регистратора продолжается до тех пор, пока не будет полностью опустошено хранилище данных или когда соединение с коммуникационным сервером не будет разорвано по таймауту (т.е., в терминах теории массового обслуживания, не будет удалено из очереди входящих сообщений коммуникационного сервера за сроком давности). При переполнении очередей модуля авторизации и диспетчера данных обработка сообщений в корневой очереди приостанавливается.
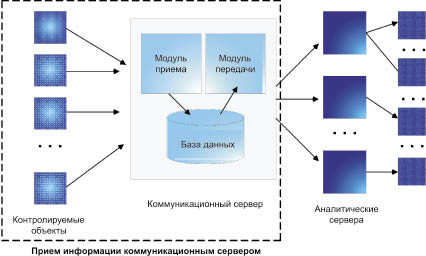
Рис. 1. Принципиальная схема передачи информации в системе непрерывного мониторинга состояния сложных технических объектов
Модельный анализ функционирования коммуникационного сервера, проводимый с учетом положений теории массового обслуживания, позволяет представить сервер как систему, размеченный граф состояний которой изображен на рис. 2.
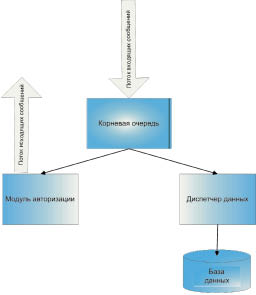
Рис. 2. Модель функционирования принимающего модуля Коммуникационного сервера
Интенсивности переходов системы из одного состояния в другое λ0, λ1, ..., λ g-1 можно интерпретировать как интенсивности возникновения заявок в системе. Аналогично величины μ0, μ1, ..., μ g-1 ‒ интенсивности переходов системы из состояния в состояние справа налево можно интерпретировать как интенсивности выполнения заявок в системе. Зная интенсивности переходов, можно найти величины p1(t), p2(t),..., pg(t) ‒ вероятности нахождения системы S в состояниях S1, S2, ..., Sg соответственно. При этом выполняется
условие
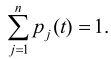 (1)
(1)
Поскольку все состояния являются сообщающимися и существенными, существует [4] предельное распределение вероятностей состояний. Получим систему уравнений для такого случая распределения вероятностей состояний системы. В стационарных условиях для каждого состояния поток, втекающий в данное состояние, равен потоку, вытекающему из данного состояния. Таким образом, имеем:
для состояния S0:
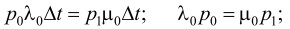
для состояния S1:
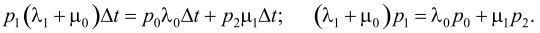
Последнее уравнение с учетом предыдущего можно привести к виду λ1 p1 = μ1p2.
Аналогично можно получить уравнения для остальных состояний системы. В результате состояния системы можно описать системой уравнений
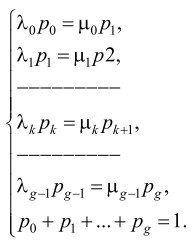 (2)
(2)
Последнее уравнение в (2) является очевидным условием (1).
Решение системы уравнений (2) имеет вид:
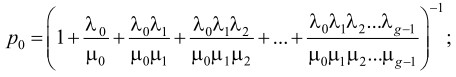 (3)
(3)
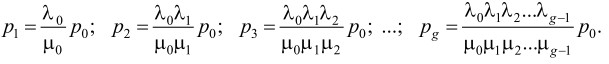 (4)
(4)
Рассмотрим модуль приема сообщений коммуникационного сервера как одноканальную систему массового обслуживания с ограниченной очередью, без ограничения нахождения заявки в очереди по времени. В системе массового обслуживания с ограниченной очередью число мест m в очереди ограничено. Следовательно, заявка, поступившая в момент времени, когда все места в очереди заняты, отклоняется и покидает систему массового обслуживания. Вероятность отказа в обслуживании заявки в такой системе равна:
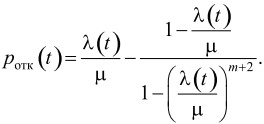 (5)
(5)
Анализируя динамику поступления и выполнения заявок в системе, необходимо отметить, что особенность системы мониторинга и оперативного анализа данных заключается в том, что необработанные сервером заявки накапливаются, увеличивая при этом поток входящих запросов. Обозначим количество поступающих заявок во входную очередь системы как A(t), количество необработанных системой заявок ‒ B(t), а количество обработанных ‒ C(t). Новые заявки, формируемые регистраторами данных, обозначим φ(t). На этой основе получимм систему уравнений:
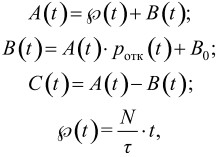 (6)
(6)
где N ‒ количество регистраторов данных; τ ‒ временной интервал между формированием заявок одним регистратором; B0 ‒ количество заявок в системе в начальный момент времени.
Результаты численного эксперимента, представленные на рис. 3, позволяют оценить уровень максимальной допустимой нагрузки на коммуникационный сервер системы при заданных технических характеристиках. Закономерности, полученные в результате проведенных натурных экспериментов (рис. 4), позволяют оценить выход системы на ламинарный режим после резко осциллирующих нагрузок.
Сравнение результатов модельного анализа с показателями работы реально функционирующей системы показывает их достаточное согласование при исследовании загруженности коммуникационного сервера, функционирующего в системе мониторинга автопарков различных предприятий.
Таким образом, разработанный метод расчета максимальной нагрузки на коммуникационные сервера систем оперативного приема и обработки информации, а также оценки их реакции на резко осциллирующие нагрузки, основанный на предложенной математической модели коммуникационного сервера системы непрерывного мониторинга состояния сложных технических объектов, позволяет провести оптимизацию загруженности информационно-вычислительного комплекса автоматизированной системы управления многоагентной технологической средой.
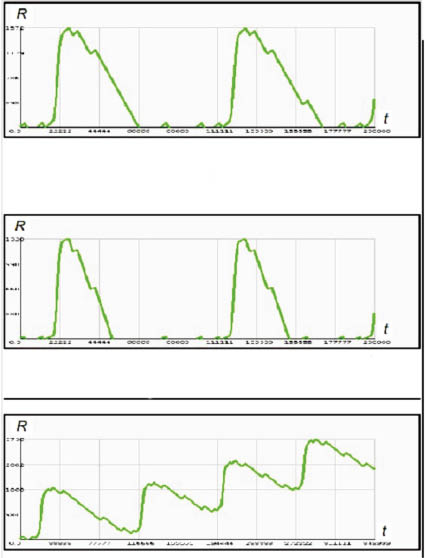
Рис. 3. Реакция серверов на резкое повышение нагрузок при разных пропускных способностях диспетчеров сообщений. Численный эксперимент
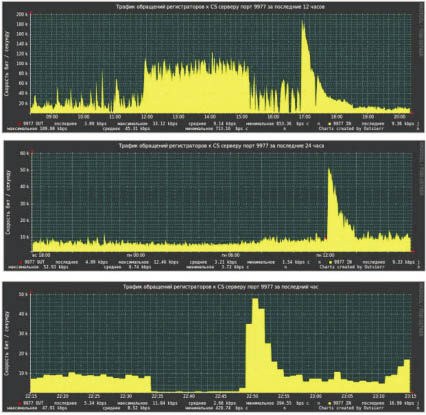
Рис. 4. Реакция серверов на резкое повышение нагрузок при разных пропускных способностях диспетчеров сообщений
Список литературы:
- Афанасьев А.П., Батурин Ю.М., Еремченко Е.Н., Кириллов И.А., Клименко С.В. Информационно-аналитическая система для принятия решений на основе сети распределенных ситуационных центров // Информационные технологии и вычислительные системы. ‒ 2010. ‒ №2.
- Афанасьев А.П., Волошинов В.В., Рогов С.В. и др. Проблемы вычислений в распределенной среде: Развитие концепции распределенных вычислительных сред // Труды института системного анализа РАН. ‒ М.: УРСС, 2004.
- Беневоленский С.Б., Жадан В.Г., Жадан И.В., Истомина Н.Л., Спыну М.В., Спыну С.К. Принципы создания программного обеспечения для систем распределенного вычисления. ‒ Современные наукоёмкие технологии ‒ 2005. ‒ №11. ‒ С. 27‒28.
- Вишневский В.М. Теоретические основы проектирования компьютерных сетей. ‒ М.: Техносфера, 2003.
- Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. ‒ М.: Наука, 1966.
- Григорьев О.Г. Модель работы сервера приложений в распределенной системе // Электросвязь. ‒ 2004. ‒ № 10.
- Хританков А.С. Модели и алгоритмы распределения нагрузки. Алгоритм на основе сетей СМО // Информационные технологии и вычислительные системы. ‒ 2009. ‒ №3.
Рецензенты:
Марсов Вадим Израилевич, д.т.н., профессор Московского автомобильно-дорожного государственного технического университета (МАДИ), кафедра «Автоматизация производственных процессов»;
Галушкин Александр Иванович, д.т.н., профессор, начальник лаборатории «Интеллектуальные информационные системы» Федерального государственного научного учреждения «Центр информационных технологий и систем органов исполнительной власти»;
Попов Федор Алексеевич, д.т.н., профессор, зам. директора по ИТ. Бийский технологический институт (филиал) ГОУ ВПО «Алтайский государственный технический университет им. И.И. Ползунова».



