Марковские цепи используются в теории массового обслуживания для расчета распределения вероятностей числа занятых приборов в системе, состоящей из n приборов с пауссоновским потоком требований и показательным законом времени обслуживания.
Цепь Маркова, используется и в качестве математической модели при изучении поведения определенных стохастических систем. Для коротких отрезков времени можно использовать вычисления абсолютных вероятностей 
. Когда же число переходов неограниченно возрастает (больше k), необходимы иные методы анализа поведения системы.
В неприводимой цепи Маркова, любое состояние Sj может быть достигнуто из любого другого состояния Si за конечное число переходов, т. е. 
, где 
, в такой цепи все состояния будут сообщающимися. Все состояния неприводимой Марковской цепи образуют замкнутое множество состояний и никакое его подмножество состояний не может быть замкнутым.
Рассмотрим Марковскую цепь с матрицей переходных состояний:
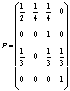
Рассматривая эту матрицу как матрицу сложности вершин некоторого графа (рисунок 1), структурный граф.
Дуги графа намечены вероятностями Pij, т. е. вероятностями перехода 
. Из определения замкнутого множества С состояний следует, что состояние не образуют неприводимой Марковской цепи, ибо состояний 0, 1 и 2 достигнуть из состояния 3 не представляется возможным. Ясно, что состояние 3 образует замкнутое множество состояний, и оно является поглощающим, т.е. состояние 3 можно считать неприводимой цепью.
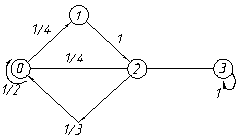
Рис. 1.
Более важной характеристики Марковских цепей применительно к задачам системного анализа является время первого возвращения в любое состояние Sj, выбранное в качестве исходного, его можно характеризовать и соответствующим числом шагов.
Введем в рассмотрение величину 
- вероятность первого возвращения в состояние Sj на m-ом шаге. Построим формулу для вычисления этой характеристики Марковского процесса. Допустим, что задана матрица переходов 
. В этом случае очевидны следующие соотношения:
,
.
Действительно, перейдя из Sj в Sj за два шага можно двумя альтернативными способами, а именно,
а) через некоторое промежуточное состояние 
,
б) перейти из Sj в Sj на первом шаге, а на втором шаге это состояние сохранить.
В первом случае вероятность перехода 
по определению есть 
, во втором случае переход системы в Sj будет повторным и его вероятность, естественно, есть произведение 
.
Таким образом,
.
Рассуждая аналогично, найдем, что
, (1)
где 
- вероятность перехода 
за три шага,
- вероятность первого возвращения в Sj на третьем шаге,
- вероятность появления Sj на третьем шаге,
- вероятность события.
Рассуждая для шага m, получим
(2)
Из (2) определяем вероятность первого появления состояния Sj на m-ом шаге
. (3)
Вероятность возвращения в состояние Sj по крайней мере хотя бы раз можно оценить по формуле
. (4)
Если можно гарантировать, что система, раз побывав в состоянии Sj, обязательно в него вернется без каких-либо ограничений на число шагов, то
.
Среднее время возвращения в состояние Sj сложно оценить средним числом шагов, требуемым для этого возврата в данной системе, т. е. величиной
(5)
Если 
, то не известно, вернется ли вообще система в состояние Sj и, следовательно, можно полагать, что 
.
Исходя из понятия «время первого возвращения в данное состояние» множество всех состояний Марковской цепи можно описать следующим образом:
1) Состояние Sj является невозвратным, если , т. е. 
.
2) Состояние Sj возвратное, если .
3) Возвратное состояние нулевое, если 
, и не нулевым, если 
, т. е. конечно.
4) Состояние периодическим с периодом Т, если возвращение в него возможно только через число шагов, пропорциональных Т, 2Т, 3Т, ..., а это означает, что если m не делится на Т без остатка, то 
.
5) Возвратное состояние является эргодическим, если оно ненулевое и апериодическим.
Из примера видно, что с ростом числа переходов в системе вектор абсолютной вероятности становится независимым от начального распределения 
, и в системе устанавливается некий предельный режим. Существование предельного распределения вероятностей состояний 
в неприводимой апериодической цепи Маркова зависит от типа ее состояний.
СПИСОК ЛИТЕРАТУРЫ:
1. Ларичев О.И. Наука и искусство принятия решений. М., 1979