В настоящее время проблема взаимосвязи "структура - свойство" весьма актуальна. Число полученных веществ непрерывно возрастает. Экспериментальное определение физико-химических свойств нередко сопряжено со значительными техническими трудностями и требует больших затрат материальных средств, квалифицированного труда, времени, да и не всегда возможно. Наличие надежных расчетных методов исследования позволяет предсказывать характеристики вещества (прежде, чем оно синтезировано, а свойство измерено) и тем самым выбирать из многих (еще не изученных и даже не полученных) соединений те, которые (согласно прогнозу) удовлетворяют поставленным требованиям. Это закладывает научные основы создания новых веществ и материалов с заранее заданными свойствами.
За последние десятилетия в теоретической химии широкое распространение получили представления топологии и теории графов. Они полезны при поиске количественных соотношений "структура - свойство" и "структура-активность", а также в решении теоретико-графовых и комбинаторно-алгебраических задач, возникающих в ходе сбора, хранения и обработки информации по структуре и свойствам веществ.
Изучение корреляций "структура-свойство" обычно ведется через топологические индексы (ТИ).
Известно много ТИ (см. [1-4]). Мы рассматривали такие индексы как
- Число Винера
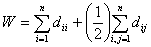
(dii , dij- элементы матрицы расстояний).
- Число
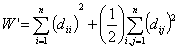
- Индекс Харари
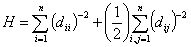
- Индекс полной смежности Бартона
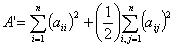
(аii , аij- элементы матрицы смежности).
- число путей длины один
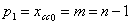 ;
; - число путей длины два
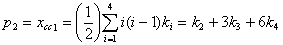
- число троек смежных ребер
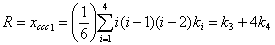
- число путей длины три
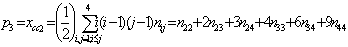
(p3 известно как число полярности р); и др.
Не все ТИ имеют ясный физический смысл и равноценны по своей корреляционной способности со свойствами. Обычно они используются в корреляционных зависимостях вида Р=f(ТИ), например,
Р = a(ТИ) + b ,
Р = a(ТИ)2 + b(ТИ) + с,
Р = b(ТИ)a,
Р = aln(ТИ) + b ,
Р = a(ТИ)1+b(ТИ)2+...+n(ТИ)n+с
и т.п. Здесь а, b, с - некоторые параметры (не следует путать их с параметрами аддитивных схем.), подлежащих определению.
Топологические индексы могут также применяться как числа параметров в построении аддитивных схем. Лучшие результаты получаются при использовании не отдельных ТИ, а их определенных совокупностей.
Например, для алкилсиланов имеем,
![]() ,
,
В табл. 1 представлены, найденные методом наименьших квадратов (МНК) значения энтальпийных параметров и результаты расчета энтальпий образования ряда алкилсиланов по указанным выше схемам.
Из таблицы видно, что в зависимости от полноты учета влияния несвязанных атомов согласие между рассчитанными и экспериментальными значениями ΔfН0(г, 298 К), как и следовало ожидать, улучшается. Существенное улучшение согласия расчёта с экспериментом начинается с учёта невалентных 1,2-взаимодействий.
Рассчитанные величины, в общем, согласуются с экспериментальными и позволяют предсказать (в пределах ошибок опыта) недостающие значения свойств членов исследуемого ряда.
Таблица 1. Параметры схем и результаты расчета энтальпий образования алкилсиланов (кДж/моль) в разных приближениях
|
Пара- метр |
Значения параметров оценки ΔfН0 (г, 298 К) |
||||
|
3 |
6 |
8 |
10 |
12 |
|
|
а0 bcc bcsi
Δccc Δccsi
ωcc ω´cc |
-4,615 -3,029 -39,600 |
13,025 -19,619 -89,936 -17,039 15,917 9,662 |
14,145 -27,443 -96,659 -8,903 24,910 16,448 -9,006 -1,770 |
16,885 -27,750 -75,689 -111,787 -17,330 -9,620 4,674 119,192 10,242 139,507 |
18,058 -29,863 -76,789 -79,552 -11,355 -11,827 10,155 90,831 14,782 84,179 6,650 -7,650 |
|
emax |
26,2 53,6 |
19,4 -60,2 |
19,5 -59,4 |
6,0 18,3 |
3,7 -14,4 |
По значениям 12 параметров табл. 1 выполнен расчёт энтальпий образования алкилсиланов от С1 до С6 [5]. Нами также для алкилсиланов были построены диаграммы «Свойство Р-ТИ», «Свойство Р - номер изомера» и ТИ - номер изомера», позволяющие просто и наглядно оценить корреляционную способность [6].
СПИСОК ЛИТЕРАТУРЫ:
- Виноградова М.Г., Папулов Ю.Г., Смоляков В.М. Количественные корреляции «структура свойство» алканов. Аддитивные схемы расчета. Тверь, 1999. 96 с.
- Химические приложения топологии и теории графов/Под ред.Р.Кинга. М.: Мир,1987.560 с.
- Применение теории графов в химии/Под ред. Н.С. Зефирова и С.И. Кучанова. Новосибирск: Наука, 1988. 306 с.
- Станкевич М.И., Станкевич И.В., Зефиров Н.С. Топологические индексы в органической химии//Успехи химии. 1988. Т.57, №3, С.337-366.
- Виноградова М.Г., Салтыкова М.Н. Теоретико-графовой подход в построении расчетных схем алкилсиланов//Вестник ТвГУ. 2007, №2(30), С.70-75.
- Виноградова М.Г., Салтыкова М.Н. Диаграммы в корреляциях»Структура-свойство» алкилсиланов//Вестник ТвГУ. 2007, №15(43), С.31-38.



