Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

К обратным задачам теории потенциала относятся следующее:

- задача определения области и плотности (задача 1),

- задача плотности (задача 2).

Наиболее сложной является задача 1.

Дадим ее постановку следующим образом (в случае объемного потенциала):

Пусть h(x) - гармоническая функция, заданная в окрестности бесконечности и 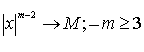 и [h(x) - M ln(x)] → 0; m= 2 (эту функцию в дальнейшем будем называть допустимой).

Пусть h - допустимая гармоническая функция, заданная вне T₀. Требуется определить измеримое множество Т,  такое, что h(x) = U (x,μ,T), x , где μ -мера определения в R^m.

1. Обозначим  внешний объемный потенциал Т, такое же обозначение сохраним и для потенциала, мера которого имеет плотность в смысле меры Лебега, будем также обозначать через μ, где   ,  x,y ∈ R^m.  потенциал простого слоя, ∂T - граница множества Т.

Замечание. Во многих постановках данной задачи требуется, чтобы Т была односвязная жордановая область, причем область T₀  не задается. В работе [3] показано, что в таком варианте задача, как правило, не имеет решения, причем решение задачи существенно зависит от глубины «аналитического» продолжения функции h.

Для данной задачи в «основном» различными авторами (см., например, [1, 2]) была рассмотрена задача «в малом», т.е. при дополнительных предложениях, одно из которых состоит в том, что гармоническая функция «близка» к заданному потенциалу. Эта задача изучена полностью. Доказана единственность решения этой задачи. Для бигармонического потенциала оказалось, что задача может и не иметь решения. В общем случае задача частично рассмотрена в [4], а подробно в работе [3]. В работе [3] эта задача решена в классе односвязных областей для объемного потенциала, а для потенциала простого слоя и в случае многосвязных областей. В этой статье мы коснемся результатов, полученных в работе [3], а также ряд других результатов. Данные результаты справедливы и для полигармонических потенциалов.

При постановке задачи можно рассмотреть такие случаи, когда мера определения только в области D ⊂ R^m ; в этом случае мы будем писать Т, .

Приведем вначале результат, полученный в [3]. Пусть  в окрестности точки x ∂T  не является аналитической поверхностью; в случае  в окрестности точки x, ; .

Сформулируем для объемного потенциала результат в виде теоремы.

Теорема 1. Если область Т односвязная, то решения задачи для положительных мер, вообще говоря, не существует, при этом, если , то множество функций, для которых не существует решения в классе односвязных жордановых областей Т, плотно во множестве тех функций, для которых решение задачи существует.

Приведем пример функций, для которых в Т решения задачи не существует [см. 3]. Пусть Ŋ ={Т∈ R^m /  R (T) = ∂T} Т - односвязная жорданова область, f(x) -аналитическая функция, такая, что  Ŋ. Тогда для h(x)=U(x;f;T),x , решения задачи не существует.

Используя данный класс гармонических функций, доказывается, что этот класс функций плотен для тех функций, для которых решение задачи существует.

В случае μ(х) ≥ а, а>0, данный результат верен и для многосвязных областей для потенциала простого слоя, если

h(x)=аV(x;1;T),x , T ∈ Ŋ ,                            (1),

где T - выпуклая область.

Правда в этом случае множество таких функций уже не будет плотным во множестве функций, для которых существует решение задачи.

Приведём класс многосвязных областей (множеств), для которых можно построить гармонические функции, для которых не существует решения задачи. Обозначим

Λ_c ={T;m(T) ≥  cl(d(T)},                                             (2)

где l(dT) - площадь (длина dT) и h удовлетворяет (1) при а<0, T ∈ Ŋ .

Тогда в Λ_c решение задачи для h не существует.

Рассмотрим семейство функций , , где , Т - выпуклая область, .Тогда в Λ_c для функции h(x) не существует решения задачи.

Заметим, что  плотно в множестве всех односвязных измеримых множеств. С другой стороны, пересечение класса данных функций h(x) есть пустое множество и, поэтому, остаётся открытым вопрос о существовании решения обратной задачи в классе многосвязных множеств.

Если мы избавимся от условия μ ≥ а для потенциала простого слоя, то решение в  Λ_c  может существовать для μ ≥ 0, если мы попробуем выполнения условия на μ (∂T) ≥ сl(∂T).

2. В работе [3], используя теоремы в «малом», доказано, что существует последовательность областей T_t (T₀ -заданная заранее область), что и для h и для произвольной допустимой аналитической функции μ верно равенство

, ,                            (2)

где T_t регулярная аналитическая поверхность, μ_t>0 если  (и даже , что, по-видимому, указывает, что плотность μ была взята «малой»), причём

.

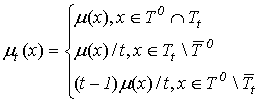Следствие. Для любой допустимой функции существуют последовательности областей T_t и кусочно-постоянные функции μ, что

,

при этом μ_t можно взять следующими:

.

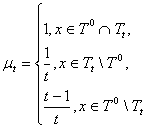Из равенства (2) и теоремы сделаем следующие выводы. Пусть для h μ не существует решение задачи. Какие видоизменения задачи можно сделать, чтобы решение задачи существовало? Для произвольной области Т зададим класс плотностей μ_t для заданной области T⁰, где t -некоторые числа. Поставим задачу определения области T_t по значению h . Тогда существует значение а > 0, что при  t  ∈ (0,a) решение задачи существует и единственно, т.е. для h справедливо равенство (2) и тем самым мы решили задачу в другой постановке. Кроме того мы установили какое преобразование можно осуществить над функцией μ, чтобы решение задачи существовало.

Рассмотрим другой подход к решению задачи. Пусть μ>0 -аналитическая функция, h(x)=MΩ (x,0)+g(x), │ x│^m-2 g(x)→0, │x│→∞.

Покажем, что найдутся области Т₁, Т₂ и число с>c⁰, что

h(x)= c(U(x; μ, Т₁)  -  (U(x; μ, , Т₂)),x ∉  Т₁,  ∪ Т₂                     (3),

Действительно, пусть Т₂ такая область, что h(x),U(x; μ, , Т₂), аналитически продолжаются до области Т₀ , Т₀ ⊂ Т₂ (в качестве Т₂ можно взять шар (круг)). Рассмотрим h₁ (x)=h(x)/c+U(x; μ, , Т₂), x ∉  Т₂ . Выберем с так, что для h₁ (x) выполняются условия теоремы существования в ´´малом´´, то есть h₁ (x)=U(x; μ ; Т₁) ,x ∉ Т₁ ∪ Т₂ . Из этого соотношения получаем равенство (3) для h (x) .

В равенстве (3) выделяется случай Т₂ ⊂ Т₁ , при котором h(x) представляется в виде потенциала двухсвязной области. Вообще говоря, это не так. Если мы берем Т₂ так, что на ∂ Т₂ ∂ μ / ∂ n+K μ ≥ 0 , то такое же представление верно и для потенциала простого слоя.

Рассмотрим ряд частных случаев. Пусть существуют число c и односвязная область T , что

U(x; μ ,Т)=с Ω(x,o),),x ∉ Т.                                (5)

Если Т - круг (кольцо), то μ(х)=К+ß(х) (К=const.), ß(х) создает нулевой потенциал, при этом если Т₁ (3), то для выполнения (5) достаточно чтобы μ(х)/К было близко к единице.

Из теоремы существования задачи в ´´малом´´ следует, что тогда существуют области T и для значений c, расположенных в интервале, содержащим данное значение. Покажем, что найдется число M₀ , что при M>M₀ h(x) можно представить в виде внешнего потенциала односвязной области Т₁ . Рассмотрим то значение c ,при котором существует такая область, что выполнено (5). Пусть функция h₁ (x)=cg(x)/M+c Ω(x,o), где g(x) аналитически продолжается через область Т. Существует число K ,что при M>Kс функция h₁ (x) удовлетворяет теореме существования в ´´малом´´ и отсюда h(x)=M/c U(x; μ ; Т₁) ,x ∉  Т₁.

В случае μ=1 можно уточнить равенство (3), а именно можно доказать справедливость равенства h(x)=U(x; μ₁ , Т₁₎ ,x ∉ Т₁ , где μ₁ =c₁ , x ∈ Т₁ Т₂ , μ₁ =c₂ , x ∈ Т₁, Т₂ некоторый шар (круг), Т₂ ⊂ Т₁ , c₁ определяется как в начале пункта. Т₂ -произвольный шар и следовательно c₂ определяется в зависимости и от Т₁ Такое же представление справедливо и для потенциала простого слоя, то есть любая гармоническая функция представлена в виде потенциала двухсвязной области, причем внутренняя компонента ограничивает некоторый шар (круг) и плотность потенциала, постоянна на каждом компоненте.

Обратим внимание на то, что если g(x) продолжается аналитически через границу шара (круга) массы M (в случае потенциала простого слоя ´´массы M сферы (окружности)), то для h(x,a)=M Ω(x,o)+ag(x), найдется такое значение a₀, что при  | a | ≤ a₀ существует решение обратной задачи для единичной плотности.

Данные рассуждения приводят к ряду проблем, требующих дополнительного изучения. Отметим, что при решении задач прослеживается связь решения с глубиной аналитического продолжения функции g(x). Заметим, что если (5) выполнено для многосвязной области Т, то предыдущие результаты сохраняются и в данном случае.

Если для μ выполнено (3), то важную роль играет следующее неравенство │g(x)/М│≥  a. При этом решение задачи существует при достаточно больших α для функции h . В свою очередь α зависит от глубины аналитического продолжения функции g(x).

СПИСОК ЛИТЕРАТУРЫ:

1. Исаков В.М. О разрешимости обратной задачи теории потенциалов / В.М. Исаков // ДАН СССР. - 1973. - № 2. - С. 66-74.
2. Павлов Г.А. Разрешимость обратных задач теории потенциала / Г.А. Павлов // Дифференциальные уравнения. - 1982. - № 10. - С. 172-179.
3. Павлов Г.А. О существовании и единственности решения внешних обратных задач теории потенциала / Г.А. Павлов // Дифференциальные уравнения. -1995. - № 4. - С. 122-130.
4. Чередниченко В.Г. Оценки потенциалов масс и разрешимость обратной задачи / В.Г. Чередниченко // ДАН СССР. - 1990. - № 4. - С. 820-824.