Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Алданов Е.С. 1 Тлеубергенова М.А. 1

---

1 Актюбинский региональный государственный университет им. К. Жубанова

Закон переноса физических субстанций описывается с использованием дифференциальных уравнений, где искомые функции подчинены заданным краевым условиям. Эти условия зависят от положения, в которой находится исследуемый объект. Такие уравнения можно рассматривать как операторные уравнения, действующие в конкретных функциональных пространствах. Сведения, полученные из такой постановки, могут быть применены для построения эффективных численных методов решения задач с большой практической значимостью. В данной работе рассматривается связь операторного уравнения, рассматриваемая в банаховом пространстве с квадратичным функционалом, и ее применение для построения одной модификации вариационного метода. Рассматриваемая в работе физическая задача: поперечный изгиб балки с постоянной жесткостью, которая лежит на упругом основании. Математическая модель этого процесса описывается дифференциальным уравнением четвертого порядка с заданными краевыми условиями, рассматриваемая как операторное уравнение с положительным оператором в левой части. Решение такого уравнение исследуется с помощью квадратичного функционала специального вида. Доказывается, что задача нахождения решений данного уравнения с заданными краевыми условиями эквивалентна задаче поиска минимума функционала. Далее, строится вариационный метод по минимизации квадратичного функционала, численный расчет которого дает решения исходной физической задачи. Практической значимостью работы является то, что численный расчет поиска минимума функционала легко осуществляется быстро сходящимся численным алгоритмом основанный минимизацию квадратичного функционала.

Статья в формате PDF

894 KB

положительный оператор

операторное уравнение

квадратичный функционал

минимизация функционала

1. Алданов Е.С. Построение приближенных решений задач теории упругости и теплопроводности на основе вариационного метода: автореф. дис. ... канд. физ.-матем. наук. – Алматы, 2004.

2. Власов Е.А., Зарубин В.С., Кувыркин Г.Н. Приближенные методы математической физики. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 700 с.

3. Колмогоров А.И., Фомин С.В. Элементы теорий функций и функционального анализа. – М.: Наука, 1968. – 543 с.

4. Леонтьев Н.Н. Приложение вариационного метода Власова В.З. к расчету фундаментов гидротехнических сооружений: дис. ... канд, физ.-мат. наук. – М., 1952. – 110 с.

5. Мухамбетжанов А.Т., Отелбаев М.О., Смагулов Ш.С. Об одном новом приближенном методе решения нелинейных краевых задач: Препринт ИА РК. – Алматы, 1997. – № 21. – 34 с.

Пусть A дифференциальный оператор

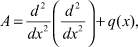(1)

определенный на множестве функций D(A) ∈ L₂ [0, 1] и непрерывные на [0, 1] вместе со своими производными до четвертого порядка включительно и удовлетворяют некоторым граничным условиям, например

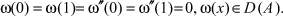(2)

И пусть q(x) ≥ 0 на интервале (0, 1).

Такое множество D(A) является линейным многообразием, всюду плотным в гильбертовом пространстве L₂[0, 1].

Определение. Линейный симметричный оператор A называется положительным, если для любого u ∈ D(A) выполняется неравенство 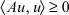, причем 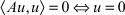[1, 2].

Из определения следует, что A –положительно определенный оператор.

Рассмотрим операторное уравнение в гильбертовом пространстве L2 [0, 1] с оператором (1)

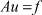. (3)

Теорема. Уравнение (3) с положительным оператором A имеет не более одного решения в D(A).

Доказательство. Допустим, что операторное уравнение (2) имеет два решения u1 и u2. Тогда Au1 = f или

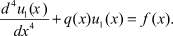
Аналогично Au2 = f или

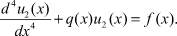
Вычи:

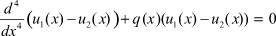
или

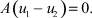
Из последнего равенства следует, что

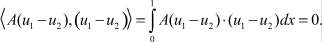
Из приведенного выше определения положительности получаем, что и это равносильно тому что

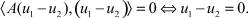
Таким образом, u1 = u2.

Уравнением (1) описывается, например, поперечный прогиб u(x) балки [3] под действием распределенной поперечной нагрузки f(x), f(x) ∈ L2(0, 1), где балка имеет постоянную жесткость на изгиб и лежит на упругом основании, реакцию которого определяет слагаемое q(x)u(x), q(x) ≥ 0 на интервале (0, 1).

При таком физическом смысле постановки задачи граничные условия отражают то, как закреплены ее концы. Так, для консольной балки с жестко защемленным левым и свободным правым концами граничные условия имеют вид

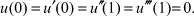
Если балка имеет на концах опоры, допускающие (в отличие от жесткого защемления) поворот ее поперечного сечения, пропорциональный в этом сечении изгибающему моменту, то в этом случае граничные условия принимают следующий вид:

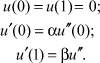
Из этих уравнений при α = β = 0 вытекают условия жесткого защемления, а при α → ∞ и β → ∞ – шарнирного опирания, и условия принимают вид (2).

Рассмотрим функционал вида

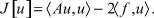(4)

Справедлива следующая теорема о квадратичном функционале.

Теорема. Для того, чтобы элемент u0 ∈ D(A) был решением операторного уравнения (1) необходимо и достаточно, чтобы квадратичный функционал (4) на u0 принимал свое минимальное значение в D(A), т.е.

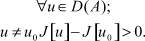
Доказательство: Необходимость. Пусть на элементе u0 функционал (4) принимает минимальное значение в D(A), т.е.

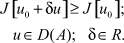
Используя свойства скалярного произведения и симметричности положительного оператора, получаем:

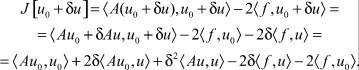
При u ≠ 0;

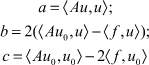
правая часть полученного выражения является квадратным трехчленом

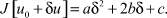
Данный трехчлен свое минимальное значение принимает при δ = 0

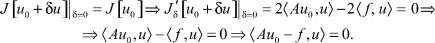
Последнее равенство означает, что элемент Au0 – f ∈ L2[0, 1] является нулевым элементом этого пространства, так как оно верно ∀u ∈ D(A) ⊂ L2[0, 1], т.е. Au0 – f = 0, а значит u0 ∈ D(A) является решением (1).

Достаточность. Функционал (4) определен при всех u ∈ D(A). Пусть u0 удовлетворяет (1): Au0 = f. Подставляя это значение вместо f в (4), получаем:

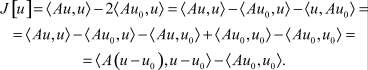
Отсюда

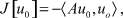
и в силу положительности оператора A имеем

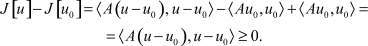
Так как

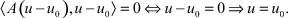
Теорема доказана.

При таком раскладе решения операторного уравнения (3) можно построить итерационный процесс [1] со скоростью геометрической прогрессии, с помощью которого можно найти минимальный элемент специального вида функционала, поиск которого является эквивалентным поиску минимального элемента функционала (4).

Введем оператор А0 следующим образом: обозначим

u(4) = v,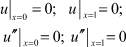

или в операторной форме

A0u = ν,

где 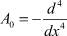 – оператор однозначно разрешим в пространстве L2(0, 1) с заданными краевыми условиями.

Тогда уравнение (3) примет вид

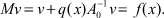(5)

Если v найдено, то u вычисляется по формуле

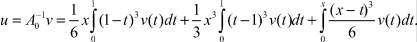
Обозначим

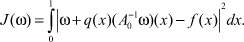(6)

При ω = ν, где ν ‒ решение (5), имеем J(ω) = 0 и наоборот.

Будем предполагать, что уравнение (5) для любой правой части f(x) ∈ L₂(0, 1) имеет единственное решение. Следовательно, из теоремы Банаха вытекает, что

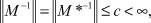(7)

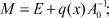где (8)

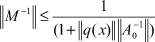
и норма 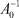 – вычисляется явно в пространстве L2(0, 1).

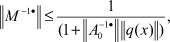
причем

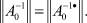
Построим итерационный процесс.

Пусть ω_n n-е приближенное решение уравнения J(ω_n) = 0.

Положим

ω _n+1 = ω_n – εω,

где ε – положительное число.

Тогда

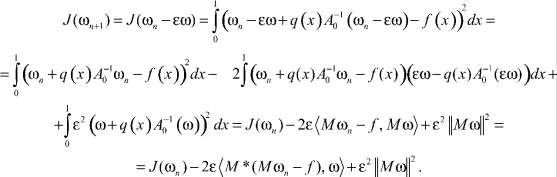
Мы воспользовались линейностью интегрального оператора A0.

Выберем

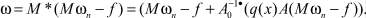
Тогда

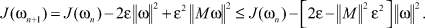(9)

В силу условия (1.11) имеем

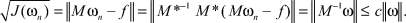
Поэтому из (1.13) следует

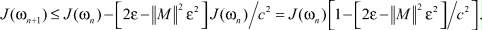
Выберем

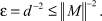
Тогда получим

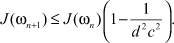(10)

Для разности ωn+1 – ωn имеем

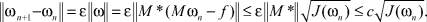
Это неравенство и (10) дают следующий результат:

Теорема 1.2.1. Пусть для любого f(x) ∈ L₂(0, 1) задача (3) имеет единственное решение 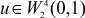, причем оператор M, определенный по (5), удовлетворяет условиям 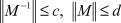, причем справедливо неравенство cd > 1. Тогда для любого ω₀ ∈ L₂(0, 1) последовательность, определяемая по формулам

,

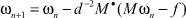сходится к решению ω• уравнения (1.9’), причем выполнены оценки

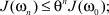
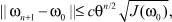
где 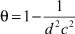. При этом функция u = A^–1 ω_• будет решением задачи (5).

Доказательство. Из (10) и последующих неравенств следует, что

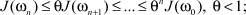
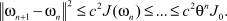
Докажем сходимость приближенного решения к решению исходной задачи:

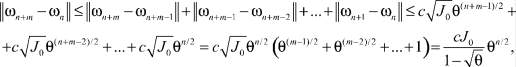
{ω_n} – фундаментальная последовательность, L₂(0, 1) – полное гильбертово пространство, тогда существует такой элемент ω•, что ωn → ω• в L₂(0, 1) и из непрерывности оператора M получим J(ω_n) → J(ω_•). Тогда из первого неравенства теоремы следует, что J(ω_•) = 0, то есть Mω_• = f и u = A^–1ω_•.

Теорема доказана.

Рецензенты:

Оразбаев Б.Б., д.т.н., профессор, Атырауский институт нефти и газа, академик ИА РК, г. Атырау;

Хасанов А., д.ф.-м.н., профессор, Актюбинский университет им. С. Баишева, г. Актобе.

Работа поступила в редакцию 21.05.2014.

Библиографическая ссылка