Использование современных технологий в области повышения надежности транспортно-технологических машин позволяет обеспечивать условия их безопасности, повысить экологическую безопасность машин, сократить расход горюче-смазочных материалов на 5–7 %, повысить долговечность составных частей автомобилей на 30–40 %, сократить простои в ремонте на 15–20 %, уменьшить расход запасных частей и материалов на 12–15 %.
Подробный анализ различных способов поддержания надежности лесотехнических средств [1–3] показал, что единственным способом поддержания жизнестойкости машины является обеспечение заданной надежности. Обеспечить определенный уровень надежности лесотехнической техники необходимо уже на стадии разработки.
Проектирование транспортной техники включает три основных звена: прочность (расчет номинальной σ(t) и предельной [σ(t)] прочности элементов конструкции); долговечность (расчет продолжительности работы в циклах N, километрах пробега L, времени работы до отказа t, срока службы H); надежность (расчет вероятности отказа R(t), вероятности безотказной работы P(t), интенсивности отказов λ(t)). Все три звена расчетного проектирования связаны между собой, как показано на схеме (рис. 1).
Каждый образец данной техники (машина или навесное устройство) представляет собой совокупность конструкционных элементов, объединенных в единую систему связями: конструкционными, энергосиловыми, информационно-управляющими. Связи могут быть описаны системами уравнений, что позволяет построить математическую модель функционирования машины.
Машина может быть представлена как совокупность систем, которые содержат в себе подсистемы (узлы и агрегаты) и элементы (детали). На рис. 2 для примера описания взаимодействия основных узлов машины, приведена укрупненная функциональная схема трелевочного трактора.
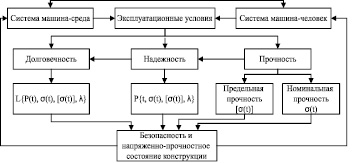
Рис. 1. Схема расчетного проектирования транспортно-технологических машин
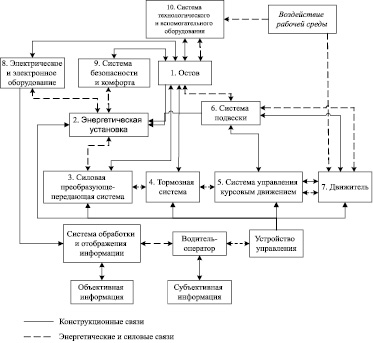
Рис. 2. Функциональная схема трелевочного трактора
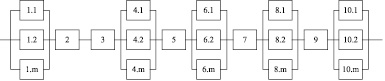
Рис. 3. Модель надежности трелевочного трактора
Каждая деталь машины обладает своей вероятностью отказа. Выход из строя любой системы машины, за исключением резервных систем, приводит к потере работоспособности машины. Для того чтобы рассчитать вероятность отказа всей системы, необходимо построить модель надежности. Модель надежности может быть представлена в виде системы последовательно соединенных блоков, которая изображена на схеме (рис. 3), где обозначения блоков соответствуют функциональной схеме машины (рис. 2).
Цель построения модели надежности состоит в том, чтобы задать надежность систем, подсистем и элементов таким образом, чтобы обеспечивался требуемый уровень надежности машины в целом. Задача оптимизации состоит в том, чтобы максимизировать показатель надежности данной техники при заданных ограничениях на количество имеющихся ресурсов или минимизировать расход ресурсов при достижении требуемого уровня надежности.
Требования по надежности к агрегатам, узлам и деталям техники зависят от таких факторов, как степень их важности, выполняемых ими функций, сложности их конструкции, изменения их надежности в зависимости от характера выполняемых ими функций.
Распределение заданной надежности P(t) по системам, подсистемам и элементам машины требует решения неравенства
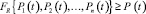, (1)
где Pj (j = 1, 2, ..., n) – заданная вероятность безотказной работы j-й структурной единицы конструкции машины; FR{...} – функциональное соотношение по надежности между структурными единицами конструкции.
Для конструкций, описываемых моделями надежности с последовательным и параллельным соединениями структурных элементов, функциональное соотношение FR(...) хорошо известно [1, 2]:
последовательное соединение –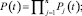 
параллельное соединение –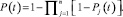 
При других конфигурациях конструкции модели надежности это соотношение является сложным, а для некоторых вариантов его даже нельзя представить в виде простых математических выражений.
Согласно [1], большинство основных моделей распределения требований к надежности основаны на допущениях, что структурные элементы системы выходят из строя независимо друг от друга, что отказ любого конструкционного элемента приводит к отказу всей машины, то есть структурные звенья в модели надежности соединены последовательно. При этом интенсивность отказов λ(t) структурных элементов определяется как
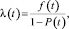(2)
где f(t) – частота отказов, определяется согласно количеству отработанных часов узла.
С учетом названных допущений и схемы, представленной на рис. 3, модель надежности трелевочного трактора, как частный случай, может быть описана неравенством
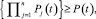(3)
где n – число структурных звеньев конструкции машины.
Если задано требование к равномерному распределению надежности по структурным звеньям конструкции, вероятность безотказной работы j-го звена определяется:
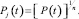(4)
Если машина имеет структурные узлы, различные по сложности и значимости их функций для прямой оценки распределения вероятностей безотказной работы по системам, агрегатам, узлам и деталям, можно воспользоваться соотношением
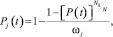(5)
где Nk (k = 1, 2, ...., m) – число модулей в структурном узле конструкции машины; N – общее число структурных узлов;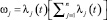 
показатель важности для j-го структурного узла конструкции машины (вероятность отказа машины при выходе из строя j-го структурного узла 
.
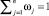Рассмотрим модель надежности проектируемого или модернизируемого образца транспортной техники, состоящей из n последовательно соединенных структурных узлов конструкции машины, для которой справедливо соотношение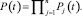 
Допустим, что требуемая вероятность безотказной работы машины P(t) должна превышать некоторое достигнутое на данной стадии проектирования значение Pi(t) i = 1, 2, ..., u. Здесь i – стадия проектирования машины, которых предполагается u. Для того чтобы обеспечить условие P(t) > Pi(t), необходимо повысить вероятность безотказной работы хотя бы одного структурного узла конструкции техники, что потребует определенных затрат (привлечение дополнительной рабочей силы, проведение обширных исследований, применение новой технологии и т.п.).
Таким образом, для каждого структурного узла конструкции машины требуется определить уровень показателя надежности (вероятности безотказной работы), который должен быть достигнут при минимальных затратах.
Примем следующую систему обозначений:
n – число структурных узлов модели надежности, описывающее проектируемый объект автотракторной техники; P(t) – требуемое значение вероятности безотказной работы машины 0 < P(t) < 1;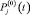 
– уровень показателя надежности (вероятности безотказной работы) j-го структурного элемента конструкции машины при существующем состоянии разработки (начальный уровень), 
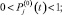Pj(t) – текущий уровень надежности j-го структурного элемента конструкции машины,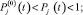 
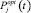– оптимальный уровень показателя надежности (вероятности безотказной работы) j-го структурного элемента конструкции машины, получаемый при минимизации общих затрат на разработку; 
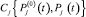– затраты, связанные с повышением показателя надежности (вероятности безотказной работы) j-го структурного элемента конструкции машины от уровня 
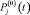до уровня Pj(t), где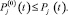 
Тогда задачу оптимизации распределения требований к надежности структурных узлов конструкции машины при минимизации проектировочных затрат можно математически сформулировать следующим образом:
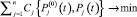(6)
при ограничении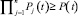 
и условии, что 
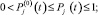(j = 1, 2, ..., n).
Каждое из n структурных звеньев конструкции машины, входящих в модель надежности, определяет этап решения задачи о распределении требований к надежности структурных узлов. Решение принимается последовательно на каждом этапе.
Для оптимизации показателей надежности основных структурных звеньев трелевочного трактора (рис. 2) используем алгоритм ЛП t-поиска [2]. Для определения пробной точки A1 проведем расчет показателей надежности для всех узлов трактора и для машины в целом. В качестве ограничения примем условие Popt(t) > P(t). Критерий качества – величина затрат на повышение уровня надежности машины (руб). Значение данного показателя желательно минимизировать.
Для решения задачи программа задает небольшие пределы варьирования значений показателей надежности структурных блоков машины. Формируется десятимерный параллелепипед П, в центре которого расположена пробная точка A1.
Подсистема генерирует множество точек и отбирает из них те, которые удовлетворяют наложенному ограничению. Оптимальным признается такое значение показателей надежности структурных блоков машины, которому соответствует минимальное значение затрат.
В параллелепипеде П при заданных ограничениях было проведено N′ = 350 испытаний. Количество точек, удовлетворяющих заданному ограничению N = 50 (эффективность отбора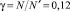 
). Результаты расчетов представлены на рис. 4.
Среди отобранных 42 точек, попавших в таблицу испытаний, необходимо выделить наиболее эффективные. С учетом указанных критериев самой эффективной оказалась точка A42. Следовательно, модель A42 не представляется возможным улучшить по всем критериям.
Из рис. 4 видно, что для достижения требуемого уровня надежности машины (P = 0,8) необходимо обеспечить достаточно высокий уровень надежности всех ее узлов, что вполне очевидно, так как по условию задачи машина состоит из достаточно большого числа узлов (N = 10), соединенных последовательно.
Вывод
Таким образом, предложенный подход позволяет при заданном уровне надежности машины определить оптимальные значения показателей надежности для каждого узла машины, учитывая важность каждого блока и затраты на проведение технического обслуживания.
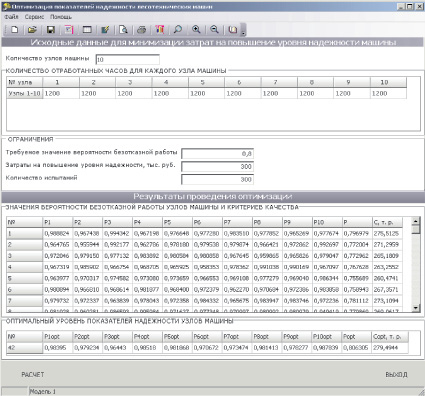
Рис. 4. Оптимизация показателей надежности ЛТС