По теории виброизоляции устройства, направленные на снижение механических колебаний, должны работать согласно эффекту нулевой жесткости, согласно которой идеальная виброизоляция абсолютно твердого тела от произвольных пространственных колебаний будет обеспечена, если в любой момент времени суммы проекций всех приложенных к нему сил на произвольные оси координат и суммы моментов относительно этих осей координат равны нулю [1]:
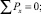 (1)
(1)
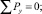 (2)
(2)
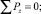 (3)
(3)
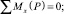 (4)
(4)
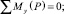 (5)
(5)
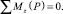 (6)
(6)
Для обеспечения участка нулевой жесткости в пределах размаха колебаний, виброизоляторы должны состоять из упругого элемента и параллельно включенного компенсатора жесткости, обладающего падающей силовой характеристикой той же жесткости, что и упругий элемент, но с обратным знаком. Таким образом, линейно нарастающая характеристика компенсируется убывающей под тем же углом относительно оси абсцисс. Это приведет к тому, что при любых пространственных перемещениях вибрирующего объекта относительно защищаемого будут соблюдаться условия (1)–(6).
В настоящее время существует много различных конструкций корректоров жесткости, представленных в разных исполнениях, основанных на принципах механики, гидравлики, пневматики [3]. Однако наиболее эффективным следует считать электромагнитный компенсатор жесткости, т.к. он обладает множеством преимуществ над предлагаемыми ранее: автоматическая подстройка на изменяющуюся нагрузку, отсутствие сил трения и дополнительной инерции. При всех своих достоинствах применение такого компенсатора жесткости затруднительно из-за значительных габаритов и дополнительного источника энергии. В [2, 6] предложено заменить основные составляющие в компенсаторе жесткости, а именно: электромагнитные катушки с сердечниками на неодимовые магниты, которые представляют собой редкоземельные постоянные магниты, состоящие из сплава неодим-железо-бор. Применение составляющих, обладающих магнитными свойствами, приводит к необходимости решения задач магнитостатики. Для решения подобных задач представляется возможным использовать программный продукт «ELCUT» компании ООО «TOR».
Для построения точной тяговой характеристики компенсатора жесткости на постоянных магнитах необходимо произвести моделирование в программной среде «ELCUT». Создание модели компенсатора позволит с допустимой погрешностью определить силу взаимодействия полей магнитов. Дальнейшее моделирование при различной величине воздушного зазора между телами позволит нам определить силу, действующую на якорь при различных его перемещениях относительно неодимовых магнитов. Эти данные станут основой для построения необходимой силовой падающей характеристики компенсатора жесткости относительно положений якоря на оси.
Данная программа позволяет проводить инженерный анализ и моделировать методом конечных элементов (МКЭ) как двухмерные, так и трехмерные модели различных магнитов, а также компенсаторов жесткости на их основе. Возможности «ELCUT» позволяют определить необходимые свойства и параметры магнитных полей как электромагнитов, так и постоянных магнитов [5]. Данная программа рассматривает неодимовый магнит как элемент, обладающий магнитной проницаемостью, коэрцитивной силой и остаточной индукцией. В системе можно найти напряженность магнитного поля в любой точке пространства около моделируемого объекта, его индукцию, силу и ее направление методом интегрирования по контуру элемента. Одновременно с вышеперечисленным имеется возможность построения графиков изменения индукции, напряженности, магнитной проницаемости и количества энергии вдоль пространственной оси [4].
Используем компьютерную программу «ELCUT» для моделирования цилиндрического неодимового магнита марки N42 и анализа его магнитных свойств.
При моделировании использованы исходные данные:
радиус магнита (стального цилиндра): 2,25 см;
высота магнита (стального цилиндра): 2 см;
остаточная магнитная индукция: 1,36 Т;
коэрцитивная сила магнита: 955 кА/м;
относительная магнитная проницаемость среды: 1;
относительная магнитная проницаемость стали: 1000;
расстояние между магнитом и магнитом (сталью): 1 см.
Первый шаг при моделировании магнитной системы элементов компенсатора жесткости – это построение магнитного поля элементов. На рис. 1, 3, 4 представлены форма и величина магнитных полей, создаваемых: неодимовым магнитом, взаимодействием магнита, стального цилиндра и двух магнитов. На рисунках приведены модели цилиндрических тел, представленных с помощью области с магнитной проводимостью, коэрцитивной силой и остаточной индукцией, причем нижняя граница представляет собой ось вращения этих тел, что позволяет моделировать участок магнитных тел, а полученный результат представляет собой параметр, справедливый для всего тела.
Из рис. 1, 3, 4 видно, что картина магнитного поля в зависимости от параметрических данных изменяется: один магнит, взаимодействие со стальным цилиндром или другим подобным магнитом. Это обусловлено разницей магнитных проводимостей, а также распределением векторов индукции и напряженности, создаваемыми составляющими устройств.
Рассмотрим подробнее эти задачи. Система моделирования «ELCUT» позволяет представить вектор магнитной индукции для одного магнита, а также представить график распределения магнитной индукции вдоль оси. Результаты представлены на рис. 1, 2.
График зависимости, представленный на рис. 2, позволяет заранее рассчитать величину индукции магнитного поля вдоль оси или по контуру. Также можно построить модель поля, создаваемого двумя одинаковыми магнитами со встречно направленными векторами индукции и напряженности магнитного поля, результаты представлены на рис. 3. На основе данной модели можно получить направление и величину векторов индукции и напряженности, а также силы, действующей на эти магниты. Для получения результатов выполнено моделирование двух магнитов по представленным ранее параметрам, с измененным направлением коэрцитивной силы одного из магнитов.
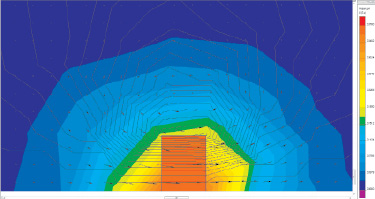
Рис. 1. Распределение и векторы магнитной индукции
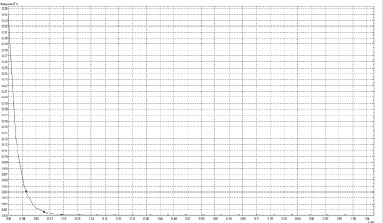
Рис. 2. График распределения магнитной индукции вдоль оси цилиндрического магнита
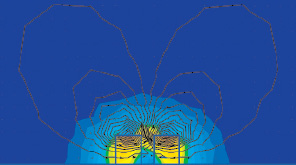
Рис. 3. Распределение и направление векторов индукции
Параметры, получаемые из программы, – точные данные взаимодействия двух магнитов, которые позволяют достаточно точно подобрать необходимое количество магнитов для создания нужной силы их взаимодействия (отталкивания/притяжения), что позволяет подобрать упругие элементы необходимой жесткости для создания компенсатора жесткости с необходимыми характеристиками.
При моделировании магнитов данная программная система позволяет исследовать ферромагнитные материалы, такие как железо и сталь. Результаты моделирования взаимодействия стального цилиндра и неодимового магнита представлены на рис. 4, 5. На этих рисунках показаны линии магнитного поля, создаваемого при взаимодействии магнита и стали, также изображены векторы индукции и напряженности магнитного поля. Данная модель, как и предыдущая, позволяет определить направление и величину вектора силы взаимодействия стали и магнита.
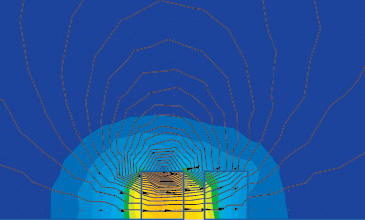
Рис. 4. Распределение и векторы магнитной индукции поля магнита и стального цилиндра
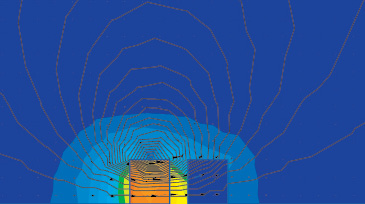
Рис. 5. Распределение и векторы напряженности поля магнита и стального цилиндра
На приведенных рисунках видны линии сетки элементов, построенные в программе. Данная сеть элементов строится автоматически и является основой для решения задач магнитостатики методом конечных элементов. Суть этого метода заключается в том, что область, для которой решаются дифференциальные уравнения, разбивается на конечное количество подобластей (элементов). В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи.
Исходя из результатов исследований, можно сделать вывод, что программный продукт «ELCUT» эффективен для использования решения задач магнитостатики, к которым и относится разработка компенсатора жесткости на неодимовых магнитах. Полученные данные при моделировании взаимодействия различных магнитных элементов станут одной из основ для проектирования компенсаторов жесткости на неодимовых магнитах.
Работа проводится при поддержке гранта РФФИ № 14-01-31386 мол_а.



