Особенностью управления технологическими роботами (ТР) при действии внешних связей является разрывность законов управления. С точки зрения взаимодействия алгоритмов управления позиционно-силовые системы управления (ПСУ) представляются в виде независимого (раздельного), согласованного (совместного) и комбинированного (связанного) управления [4].
Одним из важных условий надежной работоспособности ТР является условие устойчивости их работы на границе свободной зоны, т.е. в момент контакта инструмента и обрабатываемой поверхности. Обычно устойчивая работа систем управления ТР в свободной зоне обеспечивается, поэтому при проектировании электроприводов (ЭП) ТР необходимо проводить анализ устойчивости в режиме работы на «упор» [5] и влияния переключения структуры на условия возникновения автоколебаний.
Структурная схема ЭП при работе на «упор» и переключении структуры по сигналу с датчика моментов представлена на рис. 1, где обозначено
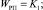
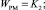
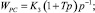
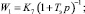
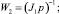
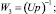
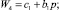
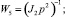
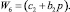
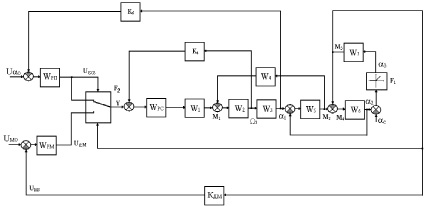
Рис. 1. Структурная схема привода с переменной структурой
Исследование нелинейной системы (рис. 1) может быть проведено с использованием метода гармонической линеаризации [2]. Для исследования периодических колебаний ЭП в режиме переключения структуры исходную структурную схему привода представляют в виде линейной части (ЛЧ) и эквивалентного нелинейного элемента (ЭНЭ) [3]. ЭНЭ содержит два нелинейных элемента НЭ1 – нелинейность типа «упор» и НЭ2 – логическое переключающее устройство (ЛПУ), соединенные между собой линейными звеньями.
Работу ЛПУ можно условно разделить на два режима: первый – переключение структуры с позиционной на моментную по сигналу M3(t), второй – переключение структуры с моментной на позиционную по сигналу Uea(t), определяющему ошибку по положению. Второй режим соответствует работе при постоянном контакте рабочего органа с поверхностью объекта работ, т.е. в линейной зоне нелинейности F1. Работу блока в этих режимах можно описать следующими выражениями:
1 режим
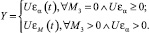(1)
2 режим
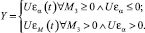(2)
Рассмотрим вначале первый случай (1). Блок переключения структуры ЛПУ представим в виде двух параллельно включенных коммутирующих элементов (КЭ) А и В, которые действуют следующим образом. Если имеется контакт рабочего органа (РО) с объектом работ (ОР), то замкнут КЭ А, а если контакта нет (М3 = 0), то замкнут КЭ В.
Полагаем, что Ua0 = 0, UМо = 0, и определим характеристики ЛПУ элементов на границе свободной зоны
A)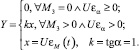 
В)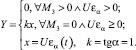 
Коэффициенты гармонической линеаризации для КЭ А определяются по формулам [3]:
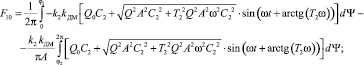
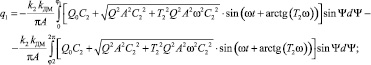
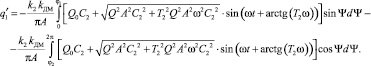
Коэффициенты гармонической линеаризации для КЭ В имеют вид
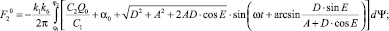
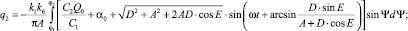
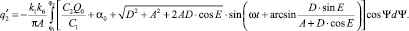
Рассмотрим теперь второй режим, описываемый выражением (2). Блок переключения структуры аналогичным образом представлен в виде двух параллельно включенных коммутирующих элементов С и Д, которые действуют следующим образом. Если при наличии контакта РО с ОР ошибка по положению отрицательная, то замкнут КЭ С, в противном случае замкнут КЭ Д.
Так же как и в первом режиме, полагая, что Ua0 = 0, Uмо = 0, a2 = aс + A∙sin wt определим характеристики коммутирующих элементов:
С)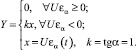 
D)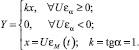 
Коэффициенты гармонической линеаризации для КЭ С:
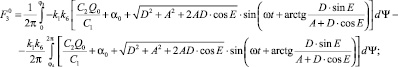
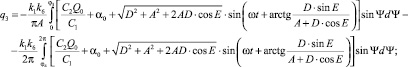
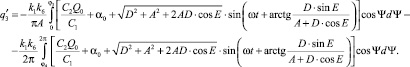
Коэффициенты гармонической линеаризации для КЭ Д:
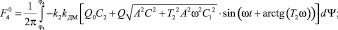
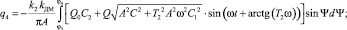
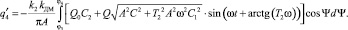
Из анализа частотных характеристик определено [1], что в первом режиме введение нелинейного звена ЛПУ уменьшает устойчивость системы, так как его ФЧХ имеет отрицательный фазовый сдвиг в области средних частот. С увеличением частоты уменьшается амплитуда сигнала, проходящего через нелинейный элемент. С ростом амплитуды коэффициент усиления нелинейного звена (КЭ А) увеличивается и увеличивается отрицательный фазовый сдвиг. Для КЭ В, наоборот, уменьшается коэффициент усиления и уменьшается отрицательный фазовый сдвиг. Во втором режиме ФЧХ имеет в основном положительные фазовые сдвиги и c увеличением частоты уменьшается усиление нелинейного звена, что повышает запасы устойчивости в нелинейной системе.
Таким образом, только в первом режиме работы ЛПУ может ухудшаться устойчивость нелинейного привода. Из анализа частотных характеристик определено [5], что в первом режиме введение нелинейного звена ЛПУ уменьшает устойчивость системы, так как его ФЧХ имеет отрицательный фазовый сдвиг в области средних частот. С увеличением частоты уменьшается амплитуда сигнала, проходящего через нелинейный элемент. С ростом амплитуды коэффициент усиления нелинейного звена (КЭ А) увеличивается и увеличивается отрицательный фазовый сдвиг. Для КЭ В, наоборот уменьшается коэффициент усиления.
Для качественного анализа колебательных движений в ЭП второго порядка с переменной структурой целесообразно воспользоваться методом фазовой плоскости. Cобственное движение такого ЭП описывается системой нелинейных дифференциальных уравнений:
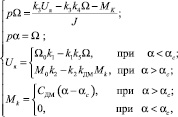(3)
где J – суммарный момент инерции, приведенный к валу двигателя.
Структурная схема ЭП, соответствующая системе уравнений (3), показана на рис. 2.
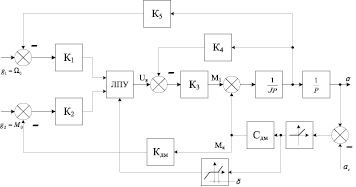
Рис. 2. Структурная схема двухканального ЭП с переменной структурой
При a < ac из (3) получаем уравнение вида
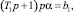(4)
где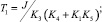 
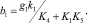
Проинтегрировав уравнение (4), получим уравнение фазовых траекторий
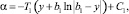
где C1 – постоянная интегрирования.
При a > ac из (3) получаем уравнение динамики привода:
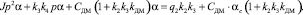
Вводя новые обозначения
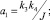
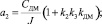
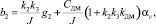
преобразуем это уравнение к следующему виду:
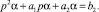(5)
При условии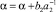 
это уравнение совпадает с уравнением
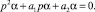(6)
Следовательно, фазовые траектории для уравнения (5) соответствуют фазовым траекториям уравнения (6) с началом координат в точке aс:
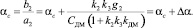
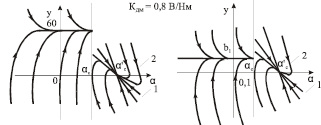
а б
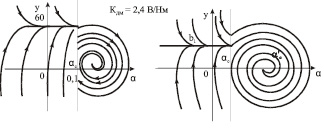
в г
Рис. 3. Фазовые портреты двухканального ЭП с переменной структурой: а – g1 = 1 В; g2 = 0,3 В; б – g1 = 0,25 В; g2 = 0,75 В; в – g1 = 1 В; g2 = 0,5 В; г – g1 = 0,25 В; g2 = 1,25 В
Здесь Da соответствует деформации датчика силы при установившемся значении Mk. Исходная система уравнений может быть представлена в виде уравнений (4) и (5). Изменение структуры приводов происходит при a = aс. Подставляя данные ЭП в уравнения (4) и (5) при aс = 0,1 рад и изменяя g1 и g2, получим фазовые траектории привода, отражающие наиболее характерные движения изображающей точки (рис. 3 а, б).
Рис. 3 в, г отражают фазовые траектории при увеличении параметров Cдм и Kдм по величине, соответственно до 1,5 Нмрад–1 и 2,4 В(Нм)–1.
Из полученных фазовых портретов ЭП можно сделать следующие выводы.
1. При a < ac качественно фазовый портрет не изменяется, движение изображающей точки изменяется лишь количественно.
2. При a > ac изменение параметров привода приводит к трем качественно отличным друг от друга фазовым траекториям:
а) a и y изменяются по апериодическому закону при следующих параметрах привода (рис. 3 а, б, прямые 1)
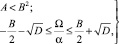(7)
где
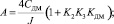
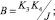
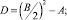
б) a и y изменяются по апериодическому закону (рис. 3 а, б, кривые 2) если
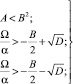(8)
в) имеют место затухающие колебания с одним или несколькими переключениями ЛПУ (рис. 3 в, г) при В2 << A.
Количество переключений зависит от соотношения корней уравнения (6) и значений b1 и Da. Если В2 << A, то привод стремится к незатухающим колебаниям, не выходя за пределы границы устойчивости.
Важными вопросами проектирования рассматриваемых ЭП являются учет времени срабатывания ЛПУ при переключении от датчика контакта, учет запаздывания сигнала с датчика контакта, а также организация скользящих режимов в двухканальных приводах с переменной структурой. Эти направления проектирования ЭП рассмотрены в [2].
Работа выполнена при финансовой поддержке РФФИ (проект № 13-08-01364).
Рецензенты:
Морозов В.В., д.т.н., профессор, заведующий кафедрой «Технология машиностроения», Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, г. Владимир;
Кобзев А.А., д.т.н., профессор, заведующий кафедрой «Мехатроника и электронные системы автомобилей», Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, г. Владимир.