Детонационное горение – основные понятия и термины
Дозвуковые режимы горения объединяются общим термином «дефлаграция». Зона реакции при послойном (меделенном) горении сосредоточена в тонком слое – фронте пламени. Пламенем принято называть область горения, испускающую видимый свет. Механизм распространения послойного горения – тепловой или диффузионно-тепловой. Воспламенение свежих слоев вещества происходит за счет их прогрева теплом, поступающим из зоны химической реакции, и за счет диффузии химически активных частиц. Скорость фронта пламени относительно исходного вещества всегда дозвуковая.
В газовых смесях фронт нормального горения (ламинарное пламя, рис. 1) распространяется со скоростями от десятков сантиметров до десятка метров в секунду. При турбулизации газового потока скорость горения и эффективная толщина его фронта возрастают за счет конвективного переноса пламени местными пульсационными течениями. Такое горение называют турбулентным (рис. 1, справа).
Начальная стадия развития экзотермической реакции в некотором объеме вещества, завершающаяся резким ростом температуры за счет тепловыделения и появления пламени, носит название воспламенения. Различают самовоспламенение, возникающее за счет самопроизвольных внутренних процессов при определенных начальных термодинамических параметрах системы и граничных условиях, и вынужденное воспламенение (зажигание), производимое с помощью постороннего источника, например, нагретого тела, электрической искры, лазера или путем подвода горячих продуктов сгорания.
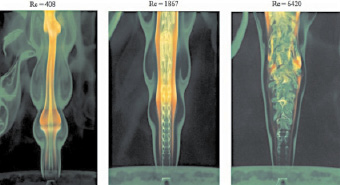
Рис. 1. Ламинарное, переходное и турбулентное горение
Законы динамической совместности на ударной волне и детонационной волне
Газодинамические разрывы (ГДР) бывают нулевого порядка Ф0 (центр волны разрежения/сжатия, скачок уплотнения, ударная волна, детонационная волна и поверхность скольжения), на которых терпят разрыв газодинамические параметры течения (P, v, ϑ) и первого порядка, называемые также слабыми разрывами (разрывные характеристики, слабые тангенциальные разрывы) Ф1, на которых терпят разрыв первые производные газодинамических переменных. Можно определить особенности (разрывы) Фi пространства газодинамических переменных любого порядка.
Условия динамической совместности (УДС) на ГДР Ф0, связывающие параметры течения до разрыва и за ним, выводятся из законов сохранения потока вещества, потока энергии, компонент потока импульса, записанных перед разрывом и за ним. В качестве параметра в этих соотношениях выступает интенсивность разрыва J (чаще всего она определяется как отношение давления за разрывом к давлению перед ним).
Дифференциальные условия динамической совместности (ДУДС) Ф0 связывают неравномерности течения перед скачком и за ним
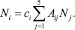
Коэффициенты Аij, сi опубликованы в работе В.Н. Ускова [1]. В целях общности в уравнения добавлены N4 = δ/y (δ = 0 в плоском течении) и N5 = Kσ (кривизна скачка уплотнения). УВС удобно изучать на плоскости ударных поляр lnJ – β, прозванных за характерный вид (рис. 2) сердцевидными кривыми (β – угол разворота потока на скачке).
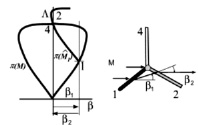
Рис. 2. Сердцевидная кривая и тройная конфигурация ударных волн
Анализ режимов медленного и детонационного горения по аналогии со скачками и ударными волнами удобно производить на плоскости адиабат (рис. 3) с помощью кривой Гюгонио (КГ), связывающей давление и удельный объем при различных режимах горения в предположении, что протяженность фронта горения (дефлаграции или детонации) мала и может быть заменена бесконечно тонким экзотермическим скачком.
Ударная адиабата связывает параметры идеального газа до ударной волны и за ней. Исходное состояние вещества до ударной волны и зоны горения характеризуются параметрами Р0, V0. Прямая, проведенная через точку Р0, V0 и какую-либо точку на КГ, называется прямой Михельсона или прямой Рэлея. На КГ имеются две точки касания с прямыми Михельсона, по одной на каждой ветви, причем верхней точке соответствует минимальная скорость распространения волны для верхней ветви, нижней точке касания – максимальная скорость волны для нижней.
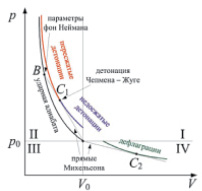
Рис. 3. Ударная адиабата (черная) и кривая Гюгонио (разноцветная)
Скорость волны для всех точек верхней ветви КГ сверхзвуковая, а для нижней ветви – дозвуковая. Таким образом, детонационным волнам соответствует только верхняя ветвь КГ. Ее называют детонационной адиабатой. Нижняя ветвь (на рис. 3 – зеленая) отвечает волнам горения, иначе, дефлаграции.
В точках касания скорость продуктов превращения относительно скачка равна местной скорости звука. Установившаяся детонация, соответствующая точке касания прямой Михельсона к детонационной адиабате, называется детонацией Чепмена–Жуге. Детонации, отвечающие участку КГ выше точки Чепмена‒Жуге (на рис. 3 – красный), называют пересжатыми, так как плотность продуктов детонации за их фронтом выше, чем в точке ЧЖ. На участке КГ ниже точки Чепмена‒Жуге (на рис. 3 – синий) детонации соответственно называют недосжатыми. Чепмен и Жуге предполагали, что реальные самоподдерживающиеся детонации отвечают именно точке касания. Но известны также различные виды устойчивой пересжатой детонации.
Из сказанного выше следуют два вывода:
– «оставленная в покое» детонационная волна стремится к детонации Чепмена–Жуге, т.е. реализовать более высокие параметры продуктов сгорания за фронтом детонационной волны возможно только в устойчивой пересжатой детонации;
– целью конструирования оптимальной УВС для организации детонационного горения с возможно более высокими параметрами является отыскание множества пересечения областей существования устойчивых экстремальных ТК УВС и устойчивых пересжатых детонаций.
О задаче конструирования устойчивой экстремальной УВС
УДС и ДУДС позволяют составить полный перечень возможных конфигураций взаимодействующих ГДР, а также исследовать область их существования, но они ничего не могут сказать о структурной устойчивости и возможных перестройках УВС при изменении параметра (J). Эта задача решается с помощью теории особенностей гладких отображений. Проектируя оптимальную УВС (в смысле достижения максимума некоторого функционала), мы ставим задачу, например, добиться максимального повышения статического давления за УВС при минимальных потерях полного давления. При этом УВС должна быть структурно устойчива к малым возмущениям.
Структурная устойчивость и возможные перестройки УВС стали предметом исследований в 80-е и 90-е годы. Допустимые перестройки УВС обусловлены выпуклостью ограничения на пространство импульсов функции Гамильтона уравнений типа уравнения Бюргерса [6]. Большой вклад в создание полной классификации возможных перестроек УВС внесли Богаевский [7], Гурбатов и Саичев [9] (1983 г.). Ими выявлено, что, начиная с размерности 2, пространства газовой динамики с четной и нечетной размерностью описываются разными типами геометрий, симплектической и контактной. Таким образом, классификация устойчивых УВС распадается на нетождественные подмножества в зависимости от размерности пространства.
Критической точкой гладкой функции называется точка, в которой дифференциал функции равен 0. Критическая точка называется невырожденной, если второй дифференциал – невырожденная квадратичная форма. Всякая вырожденная критическая точка при малом «шевелении» (Лемма Морса [4]) распадается на несколько невырожденных.
Закон Морса – функции общего положения (структурно устойчивые) имеют лишь невырожденные критические точки. Вырожденные критические точки появляются естественным образом только в тех случаях, когда функция зависит от параметра [12].
Итак, при исследовании УВС на структурную устойчивость, необходимо на плоскости поляр выявить вырожденные критические точки [5], а при исследовании возможных перестроек УВС при изменении параметра (интенсивности скачка) – дважды вырожденные точки. Соответствующие им УВС и их перестройки на практике реализоваться не должны.
Заключение
Таким образом, зная начальное положение УВС и направление ее изменения, можно точно предсказать, как она будет трансформироваться, будет ли течение газа за ней стационарным, нестационарным или колебательным. Используя этот математический аппарат, российские математики нашли все возможные последовательности перестроек ударных волн вплоть до трехмерного случая включительно. Видимо, первыми нашли подтверждение данной теории в ходе вычислительных экспериментов корейские ученые [13]. Они вычисляли трансформацию плоской волны детонации, распространяющейся по круглой трубе. В вычислениях задавались симметричные малые возмущения в начальный момент времени. Картина в точности повторяет схемы перестройки волновых фронтов, приведенные в работе В.И. Арнольда [3]. Таким образом, была создана теория и математический аппарат, достаточный для проектирования оптимальных УВС в детонационной камере сгорания, работающей как в стационарном, так и в импульсном режиме.
С помощью описанного математического аппарата автор решил задачу об отыскании диска Маха в сверхзвуковой струе, а также о колебательном движении тройных конфигураций ударных волн при взаимодействии с перпендикулярной преградой.
Рецензент:Усков В.Н., д.т.н., профессор Балтийского государственного технического университета «Военмех», г. Санкт-Петербург;
Емельянов В.Н., д.т.н., профессор, зав. кафедрой «Плазмогазодинамика и теплотехника» Балтийского государственного технического университета «Военмех», г. Санкт-Петербург;
Криштоп В.В., д.ф.-м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Университета Kwangwoon University, Korea.
Работа поступила в редакцию 05.12.2013.



