Неравномерные осадки наружного контура днища являются одной из причин снижения эксплуатационной надежности резервуара. Обычно разрушение происходит в сварных швах днища в окраечной зоне и стыке стенки с днищем [4]. Вопрос о влиянии неравномерных осадок оснований на напряженно-деформированное состояние резервуаров до конца не исследован, а полученные результаты иногда противоречат друг другу [1, 2, 3,6, 7]. На ри. 1 продемонстрированы примеры недопустимой осадки наружного контура днища РВС.
В работе [1] автор рассчитал напряженно-деформированное состояние нижнего узла резервуара при неравномерных осадках. Для этого был использован программный комплекс ЛИРА. Как выяснилось впоследствии, решение в «упругой» постановке, без учета жесткости крыши и кольца жесткости, привело к серьезным ошибкам в расчетах. Нами предлагается учитывать влияние центральной части днища, окрайки, колец жесткости, кровли на изменение напряженно-деформированного состояния резервуара при неравномерных осадках. Ранее перечисленные выше элементы не учитывались в расчетных схемах большинства авторов.
В [8] была проверена адекватность предлагаемой модели путем решения известной аналитической осесимметричной задачи в линейной постановке. Результаты численного решения, реализованного в программном комплексе ANSYS, и аналитического отличаются на величину не более 2 %, что говорит о возможности применения предложенной модели для более сложных расчетов в неосесимметричной постановке.
Расчетная схема (рис. 2) включает в себя действие нагрузки от веса стационарного покрытия и оборудования, снегового покрова и собственного веса стенки резервуара. Фундаментное кольцо является абсолютно жестким и опирается на основание со значением коэффициента постели 200 МПа/м3. В [3] указано, что железобетонное фундаментное кольцо не получает угловых деформаций с изменением жесткости основания, а лишь испытывает плоскопараллельное вертикальное смещение. Поэтому выбор значения коэффициента постели не влияет на результаты расчетов в рамках предложенной расчетной схемы. Контактное взаимодействие требует назначения контактной пары (contactpair) поверхностей или твердых тел, где один из объектов – контактный (contact), а другой – целевой (target). Зона контакта фундаментного кольца и грунтового основания, а также контакта центральной части днища и основания задается условием «упругое закрепление» (elasticsupport). Контакты стенки и окрайки (manual contact region «surface body to edge»), окрайки и фундаментного кольца (manual contact region «surface body to solid»), окрайки и центральной части днища (manual contact region «surface body to surface body») моделируются конечными элементами CONTA175 и TARGE170. На рис. 2 представлена расчетная схема.


Рис. 1. Примеры недопустимой неравномерной осадки наружного контура днища РВС
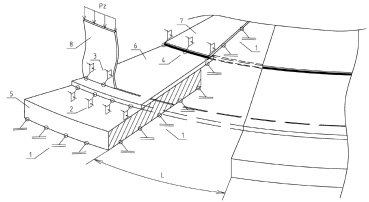
Рис. 2. Расчетная схема: 1 – упругое закрепление «elastic support»; 2 – контакт фундаментного кольца и окрайки (manual contact region «surface body to solid»); 3 – контакт листов стенки и окрайки (manual contact region «surface body to edge»); 4 – контакт окрайки и центральной части днища (manual contact region «surface body to surface body»); 5 – кольцевой фундамент; 6 – окрайка; 7 – центральная часть днища; 8 – стенка; Pz – суммарная нагрузка от веса стационарного покрытия и оборудования, снегового покрова и собственного веса стенки резервуара; L – дуговой размер зоны просадки
Геометрическая модель резервуара построена в соответствии со значениями, принятыми в типовом проекте для РВС-20000 (ТП 704-1-60). Радиус резервуара составляет 22,85 м, высота стенки 11,92 м. Толщина стенки для первого пояса – 13 мм, для 2–8 поясов – 11 мм. Листы стенки выравниваются по внутреннему краю. В предлагаемой модели стенка, окрайка, днище, кольцо жесткости представлены оболочечными конечными элементами SHELL181. Кровля моделируется балочными конечными элементами BEAM4 и состоит из 48 двутавров, профиль I35Б1 по ГОСТ 8239-89.
Материал металлоконструкций – сталь конструкционная низколегированная 09Г2С с пределом текучести σ0,2 = 300 МПа.
Рассмотрим 3 случая деформирования стенки РВС-20000 вследствие действия нагрузок, обусловленных неравномерной осадкой фундаментного кольца резервуара. В первом случае рассмотрим деформацию стенки резервуара без кольца жесткости и стационарной крыши. Во втором – с кольцом жесткости. В третьем – со стационарной крышей и кольцом жесткости. Неравномерная осадка резервуара моделируется путем вырезки сегмента фундаментного кольца размером L (рис. 3).
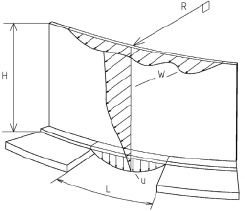
Рис. 3. Схема нагружения оболочек: L – дуговой размер зоны просадки; R – радиус резервуара; H – высота резервуара; W – радиальные перемещения стенки; u – вертикальные перемещения стенки и окрайки
Автором предлагается расчет НДС резервуара при значениях n = 2...6.
Для удобства представления результатов расчетов предлагается использовать безразмерный, принятый в теории оболочек параметр n, который учитывает размер зоны нагружения (осадки резервуара):
n = πR/L, (1)
где L – дуговой размер зоны просадки; R – радиус резервуара.
В табл. 1 представлена схема планирования эксперимента. Опыт предполагает наличие двух факторов. Первым фактором (a) является геометрическая модель резервуара с тремя комбинациями: без кольца жесткости и стационарной крыши (a1), с кольцом жесткости без стационарной крыши (a2), с кольцом жесткости и стационарной крышей (a3). Вторым фактором (b) является значение коэффициента n, при этом автором предлагается 5 возможных комбинаций: n = 2 (b1), n = 3 (b2), n = 4 (b3), n = 5 (b4), n = 6 (b5).
Таблица 1
|
Фактор a |
Фактор b |
|||||
|
I |
II |
III |
IV |
V |
||
|
I |
a1 b1 |
a1 b2 |
a1 b3 |
a1 b4 |
a1 b5 |
|
|
II |
a2 b1 |
a2 b2 |
a2 b3 |
a2 b4 |
a2 b5 |
|
|
III |
a3 b1 |
a3 b2 |
a3 b3 |
a3 b4 |
a3 b5 |
|
На рис. 4 изображена эпюра перемещений конструкций резервуара в случае a3b1 (с учетом кольца жесткости и стационарной крыши). Обозначена зона наибольших перемещений балок, которая находится над просадочной зоной.
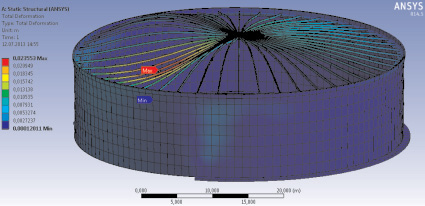
Рис. 4. Эпюра перемещений конструкций РВС
Для РВС-20000 зависимость безразмерного параметра n от величины зоны просадки выглядит следующим образом (табл. 2):
Таблица 2
|
n |
L, дуговой размер зоны просадки |
|
|
м |
рад |
|
|
2 |
36,11 |
(1/2)πR ≈ 90° |
|
3 |
24,07 |
(1/3)πR ≈ 60° |
|
4 |
18,05 |
(1/4)πR ≈ 45° |
|
5 |
14,44 |
(1/5)πR ≈ 35° |
|
6 |
12,03 |
(1/6)πR ≈ 30° |
В табл. 3 приведены результаты вертикальных, радиальных перемещений стенки резервуара в трех рассматриваемых случаях, а также максимальные эквивалентные напряжения. Максимальные радиальные перемещения (а также эквивалентные напряжения) стенки во всех случаях достигаются на максимальной высоте h = 11,92 м, причем точка наибольшего отклонения лежит на образующей, проходящей через середину вырезанного сегмента. Наибольшие вертикальные перемещения достигаются в уторном шве посередине вырезанного сегмента.
Таблица 3
|
n |
Без кольца жесткости и стационарной крыши |
С кольцом жесткости без стационарной крыши |
Со стационарной крышей и кольцом жесткости |
||||||
|
W, мм |
u, мм |
Max σэкв по Фон-Мизесу |
W, мм |
u, мм |
Max σэкв по Фон-Мизесу |
W, мм |
u, мм |
Max σэкв по Фон-Мизесу |
|
|
2 |
594 |
142,6 |
195 |
10,86 |
5,21 |
40,3 |
5,67 |
3,22 |
28,8 |
|
3 |
658 |
84,8 |
138,8 |
4,91 |
1,97 |
22,5 |
3,51 |
1,56 |
23,67 |
|
4 |
366 |
29,4 |
88,3 |
2,86 |
1,15 |
20,6 |
2,47 |
1,06 |
20,29 |
|
5 |
136 |
8,26 |
39,5 |
1,38 |
0,64 |
20 |
1,84 |
0,66 |
17,12 |
|
6 |
91 |
5,02 |
26,8 |
1,09 |
0,55 |
19,8 |
1,7 |
0,58 |
16,55 |
Выводы
– Получены результаты расчета НДС вертикального стального резервуара при неравномерных осадках наружного контура днища с учетом жесткости таких конструктивных элементов, как кольцо жесткости, окрайка, центральная часть днища, кровля.Авторами учтена физическая и геометрическая нелинейность модели.
– В случае отсутствия кольца жесткости и стационарной кровли максимальные прогибы составляют 658 мм в радиальном направлении и 142,6 мм в вертикальном направлении. При учёте кольца жесткости максимальные значения радиальных прогибов уменьшаются в 60 раз, а вертикальных – в 40 раз. При учете стационарной крыши и кольца жесткости значения радиальных прогибов уменьшаются в 120 раз, а вертикальных – в 50 раз, при этом замечены относительно большие перемещения балок кровли над просадочной зоной (до 25 мм в вертикальном направлении).
– Наличие кольца жесткости и стационарной крыши обеспечивают наименьшие значения вертикальных и горизонтальных перемещений. Даже при значении n = 2 значения радиальных прогибов не превышают 6мм, а вертикальных – 4 мм. Таким образом, для получения адекватных результатов при расчете влияния неосесимметричных нагружений на НДС резервуара необходимо учитывать приведенные выше элементы в расчетной схеме.
– Предложенная авторами модель позволяет в неосесимметричной постановке моделировать различные случаи неравномерной осадки с учетом конкретных технико-эксплуатационных условий.
– Возникает вопрос об изменении подходов к диагностике, а именно об ужесточении требований к техническому состоянию кольца жесткости и стационарной крыши, жесткость и геометрические характеристики которых значительно влияют на надежность конструкции всего резервуара в целом.
Рецензенты:Обухов А.Г., д.ф-м.н., профессор кафедры «Высшая математика», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень;
Мерданов Ш.М., д.т.н., профессор, зав. кафедрой «Транспортные и технологические системы», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», Почетный работник высшего профессионального образования Российской Федерации, г. Тюмень.
Работа поступила в редакцию 05.12.2013.



