Задачи фильтрации жидкости в пористых средах приводят к дифференциальным уравнениям с нелокальным нелинейным источником:
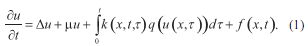
Уравнение типа(1) встречается также при описании различных процессов, в которых учитываются эффекты памяти, близкие уравнения возникает в математической биологии, где подобными уравнениями (уравнения Вольтерра) описываются некоторые процессы динамики популяции. Для уравнения (1) имеют место теоремы сравнения решений задачи Коши и начально-краевых задачи.
При математическом моделировании распределения примеси вдоль русла реки, при изучении динамики возрастной структуры популяции, а также при рассмотрении популяционной модели с пространственной диффузией приходим к краевым задачам для дифференциальных уравнений с нелокальным источником или, так называемым нагруженным дифференциальным уравнениям. В области
D ≡ {(τ, x): 0 < τ < 1,0 < x < L}
рассмотрим задачу
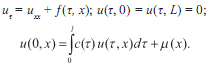
Следует заметить, что сеточные уравнения, соответствующие нагруженному уравнению теплопроводности с локальными и нелокальными условиями, приводятся к оному алгоритму, который является одним из вариантов метода циклической прогонки.



