Современное промышленное предприятие имеет в своем составе сложные технологические, теплотехнические, электрические, телефонные и другие сети. Это комплексное хозяйство является системой нового типа, где свойства системы не вытекают из совокупности свойств ее отдельных элементов. Подобные системы такой сложности рассматриваются в других направлениях науки как ценозы (биогеоценозы, техноценозы, бизнесценозы, ценозы в социальной сфере и т.д.).
Например, электрическое хозяйство крупного предприятия можно охарактеризовать следующими цифрами: максимум нагрузки достигает сотен МВт; количество установленных двигателей - десятки тыс. шт., сотни силовых трансформаторов, тысячи низковольтных аппаратов, десятки тысяч километров проводов и кабелей.
По мере роста и усложнения промышленных предприятий актуальными становятся проблемы их построения и обеспечения функционирования. Решение этих проблем основывается на объективных законах, отражающих закономерности развития природы. Законы развития техники, включающей отдельные элементы, и живой природы, состоящей из отдельных особей, имеют много общего. Поэтому представляется возможным описывать сложные технические системы на основе ценологических понятий [1].
В системе понятий «ОБЬЕКТ - СОСТОЯНИЯ-СВЯЗИ - ЗАКОН - ТЕОРИЯ» представления об обьекте, его состояниях и законах выступают основой для представлений о физическом мире, а также служат базой для выработки физических теорий и соответствующей картины мира.
Известно, что в 1877 г. при исследовании свойств отдельных особей и совокупностей живых организмов Клаус Фердинанд Мебиус ввел понятие «биоценоз». Биоценоз - совокупность живых организмов, обитающих на определенном участке, где условия внешней среды определяют его видовой состав.
Термин «техноценоз» и ценологический подход к исследованию сложных технических систем предложены в 1974 г. Б. И. Кудриным, где техноценоз определяется как сообщество всех изделий, включающее все популяции; ограниченное в пространстве и времени; имеющее слабые связи и слабые взаимодействия элементов (изделий), образующих систему искусственного происхождения, которая характеризуется несопоставимостью времени жизни ценоза и особи, невозможностью выделения однозначной системы показателей. Устойчивость системы обусловлена действием законов энергетического и информационного отборов по аналогии с живыми системами, где действует закон естественного отбора.
Кудрин Б.И. предложил использовать модель H-распределения для математического описания видового и рангового распределения
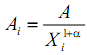
где Аi - теоретическое значение числа видов для всех I; Xi - численность популяции I; А,α постоянные видового распределения.
Применительно к промышленным предприятиям определяют, например, связь между количеством видов продукции и электропотреблением.
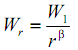
где Wr - электропотребление особи с рангом r; W1 - электропотребление особи с рангом r = 1 (максимальное электропотребление); r - ранг, β - ранговый коэффициент, характеризующий форму кривой распределения.
Для рангового распределения показатель β меняется в пределах 0,5 ≤ β ≤ 1,5. На основе зависимости годового электропо требления от разнообразия и структуры выпускаемой продукции прогнозируют параметры электропотребления, опираясь на объем выпускаемой продукции.
Отмеченные ценологические свойства промышленных предприятий констатируют устойчивость явления, проявляющегося с определенного уровня организации некоторого множества элементов с неопределенными связями: способность ценозов формировать в процессе образования и сохранять в процессе развития устойчивую структуру при наличии различных механизмов отбора. Данная теория предполагает существование некоторого идеального распределения элементов ценоза, причем стабильность системы характеризуется значением рангового коэффициента, находящегося в пределах от 0,5 до 1,5.
В работах В.И. Гнатюка предполагается, что оптимальным является такой техноценоз, который по своим функциональным показателям характеризуется максимальной энтропией и обеспечивает выполнение поставленных задач , т.е. идеальное выполнение своего функционального назначения [2].
Функциональное выполнение своего назначения и понятие идеальная техническая система уже нашли свое применение в электроэнергетике [3].
Попытаемся объяснить существование идеальной технической системы с точки зрения гармонии и золотого сечения . Предположим, что гармония и идеальное распределение видов ценоза как системы, выполняющей свое функциональное назначение, подчиняются золотому сечению, а понятие золотое сечение неразрывно связано с числами Фибоначчи.
Считается , что деление отрезка в среднем и крайнем отношении впервые было осуществлено 2500 лет назад Пифагором - великим философом и геометром древней Греции. Он показал, что отрезок единичной длины AB можно разделить точкой С на две части так, что отношение большей части (CB=x) к меньшей (AC=1-x) будет равняться отношению всего отрезка (AB=1) к большей части (CB): CB/AC=(AC+CB)/CB, или x/(1-x)=1/x. Отсюда следует алгебраическое выражение x2 + x - 1 = 0. Положительным корнем этого уравнения является (-1+√5)/2, так что отношения в рассматриваемой пропорции равны: 1/x = 1,61803... Число 1,618 обознач ается буквой F в честь древнегреческого скульптора Фидия. Единичный отрезок АВ ( 0,382+0,618=1) делится точкой С в соответствии с пропорцией
1:0,618 = 0,618:0,382 = 1,618.
Такое отношение принято называть золотой пропорцией, а соответствующее деление отрезка - золотым делением. Однако имеются факты, которые говорят о том, что о золотой пропорции знали задолго до Пифагора. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. На принципах золотого деления в древности построено много архитектурных сооружений. Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
Французский архитектор Ле Kорбюзье нашел, что в рельефе из храма фараонa Cети I в Абидосе и в рельефе, изображающем фараона Pамзеса, пропорции фигур соответствуют величинам золотого деления. Шмелев И.П. в своей работе «Основы гармонии в искусстве Древнего Египта» провел анализ резных панелей усыпальницы Хеси-Ра и показал методологию золотой пропорции. И. Ш.Шевелев установил, что сановник Хеси - Ра, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог "Тимей" посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. Платон приводит определение гармонического деления - одно из древнейших, дошедших до наших дней. «Для соединения двух частей с третьей совершенным образом необходима пропорция, которая бы скрепила их в единое целое. При этом одна часть целого должна относиться к другой, как целое к большей части».
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира, например, помпейский циркуль (хранящийся в Неаполе). Его длина 146 мм разделена шарниром на отрезки 56 и 90 мм. Этот циркуль «настроен» на золотую пропорцию
(56:90 = (-1+√5):2).
Известно, что в античной литературе золотое деление впервые упоминается в "Началах" Евклида(III в. до н.э.). Во 2-й книге "Начал" дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.
В Европе с золотым делением познакомились по арабским переводам "Начал" Евклида. Переводчик Дж.Kампано из Наварры (III в.) сделал к переводу комментарии. Cекреты золотого деления ревностно оберегались, хранились в строгой тайне, они были известны только посвященным.
В 1202 г. вышло в свет сочинение "Liber abacci" итальянского купца и математика Леонардо Пизанского (предположительно 1180-1240 г.г.), известного как Фибоначчи. Часть этого трактата составляла задача про кроликов, которая гласила: «Сколько пар кроликов рождается в год от одной пары кроликов? И сколько
пар кроликов родится в течение года, если через месяц пара кроликов производит на свет другую пару, а рожают кролики со второго месяца своего рождения?».
Решая эту задачу, Фибоначчи получил следующий результат: первая пара в первом месяце дает удвоенное потомство и в этом месяце окажется 2 пары. Из них одна пара (первая пара) рожает и в следующий месяц. То есть во втором месяце получается 3 пары; из них в следующем месяце уже две пары дают потомство, рождается 2 пары и число пар становится 5; и.т.д. Так Фибоначчи обнаружил последовательность чисел, где последующее число равно сумме двух предыдущих чисел: 0; 1; 1; 2; 3; 5; 8; 13; 21; 34, 55, и т.д., эта последовательность получила название ряда Фибоначчи. Очевидно , что начиная с нуля последовательность чисел Фибоначчи можно представить формулой:
fn+2 = fn +fn+1,
где n - порядковый номер числа Фибоначчи.
Позднее было установлено, что не только классический ряд Фибоначчи, но и любой ряд с таким же рекуррентным свойством {fn+2 = fn +fn+1}, но с другими начальными членами a, b порождает последовательность a+b, a+2b, 2a+3b, 3a+5b, 5a+8b и т.д., отношение соседних членов которой по мере удаления от начала стремится к величине F =1,618. . Влечение к "божественному сечению " (sectio divina) резко возросло в эпоху Ренессанса. Особенно большой интерес к золотой пропорции проявили ученые, зодчие и художники 15-16 веков.
В 1509 г. в Венеции была издана книга Луки Пачоли "Божественная пропорция " с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Эта книга была восторженным гимном золотой пропорции. Cреди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее "божественную суть" как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и звучит до сих пор как самое популярное. «Золотое сечение - деление отрезка на две части, при котором длина отрезка так относится к большей части, как большая часть относится к меньшей».
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропо рциях. Дюрер пишет. "Необходимо , чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются . Это я и вознамерился сделать". Cудя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Pост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Kеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя. «Устроена она так, - писал он, - что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности» [4].
С золотым сечением и числами Фибоначчи связаны целые области в культуре, науке и практической деятельности человека с древности до наших дней. Золотая или божественная пропорция , являясь чисто математическим соотношением, получила широкое применение в творениях древнерусского зодчества. К их числу следует отнести храм Покрова на Нерли, церковь Вознесения в селе Коломенское и др.
Вновь "открыто" золотое сечение было в середине XIX в. Первые работы, посвященные золотому сечению во многих явлениях биологии, появились в конце 18 - начале 19 в.в. Среди них видное место занимают труды немецкого исследователя золотого сечения А. Цейзинга [5]. Автор рассматривал золотое сечение как основной морфологический закон в природе и искусстве. Он показал, что этот закон проявляется в пропорциях тела человека и в телах красивых животных. В 1855 г. профессор Цейзинг опубликовал свой труд "Эстетические исследования". Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.
Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 / 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 / 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется муж ской. Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Справедливость своей теории ученый проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греч еские вазы, архитектурные сооружения различных эпох, растения , животные, птичьи яйца, музыкальные тона, стихотворные размеры. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга.
Г. Т. Фехнером [6] была установлена связь между психофизическим восприятием человека и "золотыми" формами предметов. Т. Кук уделяет большое внимание изучению роли логарифмической спирали в растительных и животных объектах. Им установлено, что феномен роста в биологических объектах связан со спиралями золотого сечения. О значении золотой пропорции в природе и искусстве пишут Г . Тимеринг [7], М. Гика [8] и Г. Д. Грим [9], которые приводят многочисленные примеры проявлений золотого сечения в явлениях природы и различных прикладных искусствах. Ряд Фибоначчи встречается в расположении листьев на деревьях, семян подсолнечника или сосновой шишки [10]. .
Интерес к золотому сечению сохраняется и в наши дни. В нашу задачу входит показать значение золотого сечения и чисел Фибоначчи в сфере организации технических систем по аналогии с живой природой. Если взять числовой ряд 1,0; 0,62; 0,38; 0,24; 0,15; 0,09 и т.д. (что напоминает шкалу мощностей трансформаторов), состоящий из чисел с коэффицентом 1,618 («Золотое сечение») и аппроксимировать этот ряд чисел, то получим гиперболическую кривую (рис.1), которая описывается следующей формулой [11]:
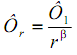
где β= 1,63 - ранговый коэффициент.
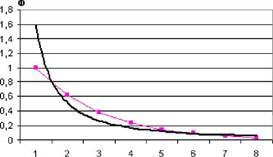
Рис.1 Гиперболическая кривая
Этим числовым рядом (H-распределение) можно описывать при ранжировании в ценозе соотношение количества видов и численности каждого вида.
На последние 10-15 лет приходится настоящий бурный всплеск исследований по проблеме золотого сечения. В эти годы в России и странах СНГ появились крупные работы в различных направлениях науки, где золотая пропорция и ее закономерности использованы как своеобразный методологический принцип, лежащий в основе анализа самоорганизующихся природных и технических систем, их структурной гармонии.
В работах А. П. Стахова, Э. М. Сороко, Ю. А. Урманцева, К. Б. Бутусова, М. А. Марутаева, О. Я. Боднара, В. Д. Цветкова, В. В. Очинского, В. И. Коробко и многих других ученых представлено множество проявлений закономерностей золотого сечения и чисел Фибоначчи в пропорциях человека, биологии, ботаники, эргономике, архитектуре, поэзии, музыке и т.д.; на многочисленных примерах из различных областей знаний показано, что свойства и закономерности золотого сечения и чисел Фибоначчи проявляются в виде принципов оптимальности в организации и функционировании различных систем.
Применение этих закономерностей для поиска оптимальных параметров функционирования систем служит одним из приемов, используемых в качестве методологической основы ценологических исследований технических систем.
Эта особенность является проявлением свойств систем ценологического типа, исследованных, в частности Кудриным Б.И. на примере многономенклатурных предприятий химической промышленности. Представляется возможным применение данного подхода для оценки количества и видового разнообразия электротехнического оборудования при проектировании, а в эксплуатации - при прогнозировании электропотребления, электроремонтов и оценке потенциала энергосбережения (сравнивая фактическое и идеальное H-распределение).
Вывод:
С учетом опыта развития живой природы, можно предполагать, что кривая на рис. 1 отражает идеальное соотношение количества видов и численности каждого вида. Поэтому при определении основных показателей и количества установленного оборудования целесообразно использовать понятие «золотое сечение» и числа Фибоначчи. Поскольку эти соотношения существуют в природе, то человек неосознанно создает техноценозы таким образом, что их оптимальная структура определяется этими постоянными.
СПИСОК ЛИТЕРАТУРЫ
- Кудрин Б.И. Введение в технетику. 2-е изд. переработ. и доп. Томск: Изд-во Томск . гос. ун-та, 1993. 552 с.
- Гнатюк В.И. Закон оптимального построения техноценозов. Калининград: КВИ ФПС РФ - ЗНЦ НТ РАЕН, 2003.- 132 С.
- Южанников А.Ю. Полезность и плата за полезность при выборе компенси-рующих устройств. Межвуз. сб. науч. трудов НЭТИ. Новосибирск: НЭТИ, 1990. С.42-45.
- Урманцев Ю. А. Симметрия природы и природа симметрии. - М: Мысль, 1974. - 229 с.
- Zeising A. Neue Lehre von den Proportionen des menschlichen Korpers. Leipzig, 1854. - 457 s.
- Fechner G. T. Vorschule der Asthetik. Leipzig: Breitkopf und Hartel, 1897. - 264 s.
- Тимеринг Г. Е. Золотое сечение. - Петроград: Научное книгоиздательство, 1924. - 86 с.
- Гика М. Эстетика пропорций в природе и искусстве. - М.: Изд. кад.арх., 1936. - 236 с.
- Грим Г. Д. Пропорциональность в архитектуре. - М.-Л.: ОНТИ,1935. - 148 с.
- Коробко В.И., Коробко Г.Н. Золотая пропорция и человек. М. Изд - во междунар. ассоциации строит. вузов: 2002.-394 с.
- Южанников А.Ю. Золотое сечение, числа Фибоначчи и ценологические параметры электропотребления промышленного предприятия. Вестн. Ассоц. Выпуск КГТУ. Вып. 12 / Под ред. А.А.Михеева. Красноярск: ИПЦ КГТУ, 2005. С.165-169.
Библиографическая ссылка
Южанников А.Ю. МОДЕЛИРОВАНИЕ ЭЛЕКТРИЧЕСКИХ ЦЕНОЗОВ И ЧИСЛА ФИБОНАЧЧИ // Фундаментальные исследования. 2006. № 11. С. 83-87;URL: https://fundamental-research.ru/ru/article/view?id=6556 (дата обращения: 22.12.2025).



