В исходной постановке задачи выделяются два основных структурных компонента разрабатываемой программной системы - сетевые узлы и связанные с ними потоки.
Рассматриваются совокупности узлов, являющихся частью среды передачи данных с негарантированной ("best-effort") характеристикой обслуживания, взаимодействующих посредством множества потоков и представимых в виде связных ориентированных графов. Требование связности этого графа подразумевает, что в совокупность попадают лишь узлы, между любой парой которых существует цепь (другие узлы и потоки между ними) их соединяющая. Рассматриваются только симплексные потоки.
На низком уровне рассматриваются подграфы, включающие один центральный узел и смежные с ним узлы (включаются только дуги инцидентные центральному узлу). Именно на этом уровне решается рассматриваемая оптимизационная задача: для всех узлов в системе определено множество классов распределяемых ресурсов
![]() ,
, ![]() ,
,
и связанных с ними ограничений. Узел занимается обработкой потоков
![]() ,
, ![]() ,
,
перераспределяя выделенные ему ресурсы R в соответствии с требованиями каждого потока.
Поток описывается двумя основными параметрами:
- входной интенсивностью l (количество блоков данных генерируемых приложением в единицу времени), в общем случае являющейся функцией времени;
- величиной задержки потока на узле назначения Dt, определяемое в момент создания потока из требования (1), и являющееся константной величиной все время существования потока.
Основное требование, предъявляемое к системе при обработке потоков, связывающее перечисленные выше параметры, выражается равенством (1):
![]() (1)
(1)
где l(t) - входная интенсивность потока, l´(t) - выходная интенсивность, Dt - величина задержки. Нарушение этого равенства трактуется как отказ в обслуживании по отношению к обрабатываемому потоку.
На основании (1) вычисляется вектор минимальных требований по каждому из ресурсов:
![]() ,
,
![]() ,
,
где Q imin - вектор минимальных требований для i-го потока. Причем:
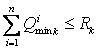 (2)
(2)
где Rk - количество k-го ресурса, доступное узлу для распределения между потоками. Нарушение требования (2) трактуется как ситуация исчерпания ресурсов и также влечет за собой отказ в обслуживании.
В качестве критерия функционирования разрабатываемой системы принято:
![]() (3)
(3)
где Pотк. - вероятность отказа в обслуживании, Pпер. - вероятность нарушения условия (1) по всем потокам, Pрес. - вероятность исчерпания ресурсов (2) по всем потокам.
В процессе работы система должна принять решение - сформировать общий вектор распределения ресурсов между потоками:
![]() ,
,![]() , (4)
, (4)
где
![]() ,
, ![]() , (5)
, (5)
причем с одной стороны вычисляемое распределение ресурсов между потоками, также как и минимальные требования, должно подчиняться неравенству (2):
![]() , (6)
, (6)
с другой, условию (1), что можно выразить так:
![]() ,
, ![]() и
и ![]() . (7)
. (7)
Далее, вернувшись к исходной постановке задачи (об эффективном управлении в сетях) и проанализировав ее специфику, следует отметить, что множество R неоднородно, в том смысле, что включает как действительные, так и целочисленные компоненты. Т.е. по сути, данное множество распадается на два:
![]() , (8)
, (8)
![]() ,
,![]() ,
, ![]()
![]() ,
,![]() ,
,![]()
![]() ,
,
где RZ - подмножество целых компонентов R, RR - подмножество действительных компонентов R, v и u - соответствующие размерности этих множеств.
Получаем, что:
- исходная задача сводится к необходимости вычисления вектора распределения ресурсов Q;
- при заданных ограничениях (6) и (7);
- с целевым функционалом (3);
- и свойством множества R (8).
А это фактически представляет собой формулировку задачи дискретного программирования в её общей форме.
Если рассматривать геометрическую интерпретацию задач этого класса, то суть их сводится к отысканию точки в гиперпространстве размерности равной числу компонентов оптимизируемого вектора. У нас согласно определениям (4) и (5) размерность множества решений D составит:
![]() , (9)
, (9)
т.е. с появлением каждого нового потока в системе сложность решения будет возрастать на величину m количества классов ресурсов. Такая ситуация фактически сводит на нет эффективность использования стандартных процедур решения задач дискретного программирования. Поэтому целесообразно понизить ее размерность, исключив каждые (m-1) компонентов введением функции свертки для потоков:
![]() ,
,![]() , (10)
, (10)
Далее необходимо переформулировать (3), (6) и (7) и решать задачу относительно введенных переменных-сверток.
СПИСОК ЛИТЕРАТУРЫ
- Кравец О.Я., Шипилов Д.В. Управление потоками в сетях интегрированного обслуживания как задача об эффективном распределении вычислительных ресурсов сетевых узлов // Технологии интернет - на службе обществу. Саратов: СГТУ, 2003.
Библиографическая ссылка
Шипилов Д.В., Кремер А.А. ФОРМАЛИЗАЦИЯ МОДЕЛИ УПРАВЛЕНИЯ РЕСУРСАМИ СЕТЕЙ ИНТЕГРИРОВАННОГО ОБСЛУЖИВАНИЯ В ВИДЕ ЗАДАЧИ ДИСКРЕТНОГО ПРОГРАММИРОВАНИЯ // Фундаментальные исследования. 2004. № 6. С. 127-128;URL: https://fundamental-research.ru/ru/article/view?id=6514 (дата обращения: 05.01.2026).



