Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Файлы

Антамошкина Е.А., Дегтерев А.С., Золотарев М.Ю.

Статья в формате PDF

262 KB

После определения состава оптимальной производственной программы важное значение имеет ее распределение по плановым периодам. Особенно актуальная эта задача для конверсионных предприятий с мелкосерийным характером производства гражданской продукции. При ее решении необходимо выполнять такие требования, как выпуск продукции в заданные сроки и выполнение годового плана производства продукции; ритмичность работы предприятия и его подразделений; минимальное количество переналадок оборудования; минимальная номенклатура изделий, одновременно находящихся в производстве [1].

Трудность решения задачи обусловлена тем, что номенклатура выпускаемых изделий обычно достаточно велика, а для значительной части изделий установлены директивные сроки выпуска. Помимо минимизации общего количества переналадки равномерно в течение всего планируемого периода, надо обеспечить равномерную загрузку соответствующих служб.

Как правило, задача оптимального распределения программы решается в предплановом периоде, но это не исключает возможности ее решения и в течение планового периода в связи с изменением номенклатурных планов предприятий, директивных сроков и т. п. В этом случае приходится учитывать, что некоторая часть изделий уже запущена в производство и перераспределение должно производится таким образом, чтобы выполнить все основные требования, предъявленные к задаче, и не допустить длительной задержки запущенных в производство изделий.

Задача оптимального распределения производственной программы предприятия должна входить в состав АСУП, так как ее решение на этапе формирования плана дает четкое представление о выпускаемых в каждом месяце изделиях, о загрузке различных групп оборудования, позволяет более качественно составить заявки на поставку материалов и комплектующих изделий, сократить время их хранения на складах, более рационально планировать планово-предупредительные ремонты оборудования и т. д.

Задача разработана для ряда машиностроительных и приборостроительных предприятий страны. Продукцию, выпускаемую этими предприятиями, можно разделить на изделия массового и крупносерийного производства и изделия серийного и мелкосерийного производства. Поэтому и решение задачи можно разбить на два этапа.

На первом этапе определяется трудоемкость изготовления одного изделия на каждой группе оборудования, рассчитываются ресурсы предприятия в каждом месяце, например, фонд времени по каждой группе оборудования с учетом планово - предупредительных ремонтов и плановых простоев. Второй этап - распределение изделий массового и крупносерийного производства. Оно производится либо пропорционально количеству рабочих дней в каждом месяце, либо пропорционально стоимости готовой продукции по месяцам. Затем корректируются все ресурсы с учетом полученного распределения, после чего распределяется серийная и мелкосерийная продукция. Для распределения серийного и мелкосерийного производства разработана экономико-математическая модель [2].

Введем следующие условные обозначения:

j - индекс партий изделий, выпускаемых предприятием. Под партией изделий понимается либо полная производственная программа для данного изделия, либо какая-то максимально допустимая ее часть;

J - множество индексов партий изделий;

i - индекс какого-то ресурса, например, фонда материалов, фонда времени работы оборудования и т.д.

I - множество индексов ресурсов;

T_ik - объем i-го ресурса в k-ом периоде, оставшийся после вычета объемов используемых под массовую и крупносерийную продукцию, изделия с директивными сроками выпуска, изделия, находящиеся в незавершенном производстве, а также на окончание обработки партий, оставшихся с (k-I)-го периода;

E_ik - допустимые отклонения i-го ресурса в k-ом периоде от T_ik.

a_ij - расход i-го ресурса на j-ю партию изделий;

j_k - множество индексов партий изделий-кандидатов для включения на выпуск в k-м периоде (j_kÎJ);

x_j=0, если j-я партия не обрабатывается в k-м периоде, в противном случае x_j=1;

F_ek - фонд времени работы e-й группы оборудования в k-м периоде;

l - индекс группы оборудования;

L - множество индексов групп оборудования;

F_ej - станкоемкость изготовления j-й партии изделий на e-й группе оборудования.

Тогда систему ограничений, составленную с учетом требований задачи распределения и наличных ресурсов можно записать в виде неравенств

В качестве целевой функции можно выбрать наиболее важное из требований задачи распределения, например равномерную загрузку оборудования т. е.

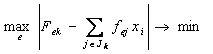
Для достижения минимальности общего количества переналадок в течение всего планируемого периода на переменные x_j необходимо наложить условие x_j =0 или x_j=1, jÎJ.

Т.е. каждая партия изделий изготовляется полностью от начала до конца, либо совсем не изготовляется в каком-то месяце.

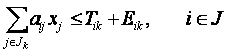
Если, во-первых, каждое двустороннее неравенство заменить двумя односторонними неравенствами

во-вторых, ввести неизвестное y, удовлетворяющее условиям

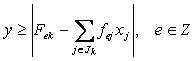
то задача сведется к решению эквивалентной задачи

y ® min

и условиях

x_j=0 или x_j=1.

Для решения задач такого вида имеются программы решения задач целочисленного линейного программирования с булевыми переменными и аддитивным алгоритмом Балаша. С помощью этой программы можно решать задачи с числом переменных до 300 и ограничений до 100.

Если задача не имеет решения, двусторонние ограничения имеет смысл заменить такими:

Тогда исходная задача сводится к решению многомерной задачи о ранце, т. е. к решению задачи вида

при

целые числа

где

Для решения таких задач могут быть применены классические методы целочисленной оптимизации, например, динамического программирования, однако ограничения на размерности решаемых задач, опять-таки делают эти методы не очень практичными.

СПИСОК ЛИТЕРАТУРЫ

1. Дегтерев А.С., Ерыгин Ю.В. Инструменты стратегического планирования инноваций на машиностроительных предприятиях оборонно-промышленного комплекса в условиях конверсии. - Конверсия в машиностроении, № 3, 2004, с. 78-83.
2. Дегтерев А.С., Нейман Г.А. Моделирование задачи оптимизации загрузки технологического оборудования . - Экономика и финансы, 2002, № 20 (22), с. 46-48.

Библиографическая ссылка