Для моделирования процесса разделения необходимо описать динамику движения частицы плотностью ρ в суспензии, движущейся в коническом, аппарате, что является важной, в том числе прикладной задачей определения оптимальных режимных и конструктивных параметров конической центрифуги.
Расчетная схема представлена на рис.1.
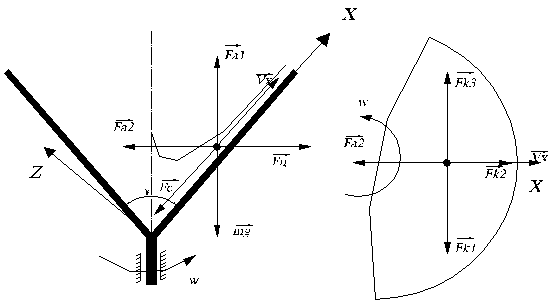
Рисунок 1. Расчетная схема к задаче о движении частицы по конической поверхности.
Начальные скорости частицы
(1)
Уравнение движения частицы в векторной форме можно записать
(2)
где 
- сила Кориолиса, которую можно разложить на три составляющие:
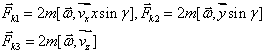(3)
В (2.15) 
- сила сопротивления среды[1]; 
- центробежная сила. 
- архимедова сила. Силу сопротивления находим по формуле Стокса[2]:
(4)
где 
- относительная скорость
(5)
Коэффициент сопротивления k может быть вычислен по формуле[3]:
(6)
В (2.19) k0- коэффициент, учитывающий количество твердой фаза в суспензии
(7)
Здесь Ж/Т- отношение объема жидкой фазы к объему твердой фазы в суспензии, 
- кинематическая вязкость суспензии.
Вязкость суспензии рассчитываем по формуле[3]:
(8)
где 
- кинематическая вязкость воды; 
- содержание твердой фазы в 1м3 суспензии, кг; 
- плотность суспензии.
(9)
Здесь 
- плотность воды, 
- плотность твердой фазы
Координатная форма имеет вид:
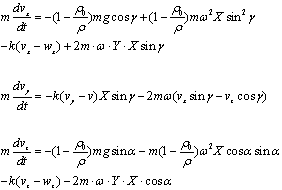(10)
Начальные условия
(11)
Решением системы уравнений (2.23) определяем зависимость координат и скоростей частицы времени:
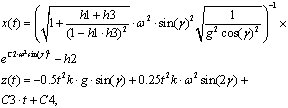(12)
где
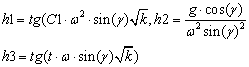(13)
Величина угла при вершине конуса γ существенно влияет на толщину слоя жидкости (2.12). С увеличением этого угла резко уменьшается толщина слоя жидкости, что затрудняет процесс разделения.
Описав динамику одиночной частицы, перейдем далее к описанию движения суспензии в целом. Предположим, что в начальный момент времени частицы твердой фазы распределены равномерно по высоте суспензионного слоя толщиной δ. Представим поток суспензии состоящим из s слоев толщиной δ/s, в каждом из которых находится 
частиц каждой фракции. Опишем движение слоя как движение частицы, находящейся внутри данного слоя, т.е. предположим, что все частицы одной фракции внутри слоя движутся по конгруэнтным траекториям. Считаем также распределение частиц внутри слоя равномерным. Предположим, что частицы не взаимодействуют между собой как внутри слоя, так и с частицами находящимися в соседних слоях и не переходят из слоя в слой. Пересечение слоев не влияет на движение частиц. Крупные и мелкие частицы, осевшие на стенку ротора, движутся по его поверхности с одинаковой скоростью, не отрываясь от поверхности. Запишем уравнения движения (2.25, 2.26, 2.40)для частиц, находящихся на границах q-го слоя i-й фракции, где q номер слоя.
Начало отсчета слоев взято от поверхности конической насадки. Для q-го слоя нижняя и верхняя границы рассчитываются по формулам:
(14)
Число не осевших частиц i-й фракции в сечении суспензионного слоя находящемся на расстоянии х от вершины конической насадки определяем из соотношения:
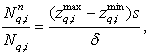(15)
где 
- число осевших частиц в q-м слое i-й фракции, 
- общее число частиц в q-м слое i-й фракции.
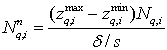(16)
Тогда общее число частиц i-й фракции, осевших в сечении суспензионного слоя, находящегося на расстоянии х от вершины конической насадки.
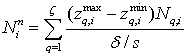(17)
Расчетная схема представлена на рис 2.11
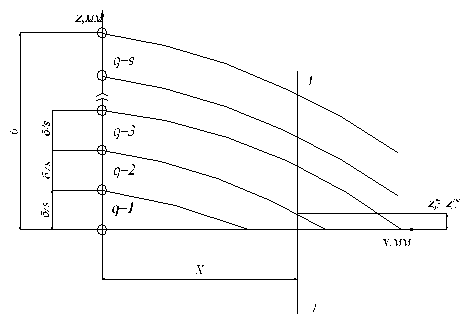
Рисунок 2. Схема расположения слоев
Разработанная математическая модель разделения суспензии на вращающейся конической насадке позволяет определить процентное содержание жидкой и твердой фаз в любом сечении суспензионного слоя.
СПИСОК ЛИТЕРАТУРЫ
- Лойцянский Л. Г. Механика жидкости и газа. Изд.5-е, -М.: Наука, 1978. 736с
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учебное пособие в 10 т. Т.VI. Гидродинамика. - М.: Наука. 1988.
- Лебедев А.Е. Математическое моделирование процесса разделения суспензий в новом аппарате применительно к их транспортированию: Дисс. ... канд. техн. наук. - Ярославль.: ЯГТУ, 2004. 128с.
Библиографическая ссылка
Лебедев А.Е., Павлов А.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА РАЗДЕЛЕНИЯ СУСПЕНЗИИ НА ВРАЩАЮЩЕЙСЯ КОНИЧЕСКОЙ НАСАДКЕ // Фундаментальные исследования. – 2005. – № 3. – С. 54-57;URL: https://fundamental-research.ru/ru/article/view?id=5857 (дата обращения: 23.11.2024).