Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы

Осипенко И.А., Снежков В.И.

В статье анализируется электронное строение оксидов семейства перовскита типа АВ_1/2В`_1/2О₃ методом сильной связи. В качестве подтверждения правильности выбора модели проведен расчет электронного строения кристалла BaYb_1/2Ta_1/2O₃ в упорядоченной фазе. Теоретические результаты находяться в хорошем согласии с экспериментальными данными по измерению электропроводности и фотопроводимости в кристаллах тройных оксидов семейства перовскита. 6с., 2 илюст.

Статья в формате PDF

165 KB

В начале и середине 20 века большое внимание уделялось исследованию свойств оксидов семейства перовскита (ОСП), имеющих элементарную ячейку типа АВО₃, где А - щелочной или щелочно-земельный элемент, В - переходной элемент. Кристаллы или керамики данного типа имеют уникальные диэлектрические, пьезоэлектрические, пироэлектрические, электрооптические и другие свойства, которые позволяют найти применение данных кристаллов и керамик в различных электронных и оптических устройствах. Синтезирование Смоленским и др. в 1958 и 1959 году тройных ОСП со структурой  и , где В - переходной элемент, а В´ - другой переходной элемент, положило начало исследованию этих керамик и кристаллов. Как показали исследования, они имеют некоторые новые интересные свойства, которые интересны для практического применения в технике. Так, например, всем хорошо известно, что электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости материала размещенного между электродами конденсатора. У титаната бария (BaTiO₃) значение диэлектрической проницаемости порядка 15000, что значительно больше значения диэлектрической проницаемости у обычных керамик или полимерных материалов которые ранее использовались в конденсаторах. Использование в качестве прослойки между электродами конденсатора титаната бария позволяет значительно сократить размеры конденсаторов и увеличить их емкость. В то же время у магний-ниобата свинца (PbMg_1/3Nb_2/3O₃) максимальное значение диэлектрической проницаемости составляет 25000, кроме того, у магний-ниобата свинца диэлектрическая проницаемость имеет менее ярко выраженную зависимость от температуры и частоты переменного электрического поля по сравнению с титанатом бария. Соответственно, использование магний-ниобата свинца вместо титаната бария позволяет улучшить рабочие характеристики конденсаторов и уменьшить их размеры. В настоящее время очень большое внимание привлечено к использованию в различных электронных и электрооптических устройствах сегнетоэлектрических тонких пленок. Например, весьма перспективным направлением использование данных пленок на основе тройных ОСП при создании сегнетоэлектрических произвольного доступа модулей памяти (FRAM´s), конденсаторов. Использование тонких пленок на основе Pb(Zr,Ti)O₃, (Pb,La)(Ti,Zr)O₃ для создания световодов, использование пленок на основе (Pb,La)(Ti,Zr)O₃ для создания оптической памяти, в производстве дисплеев, тонких пленок на основе PbTiO₃, (Pb,La)TiO₃ и Pb(Zr,Ti)O₃ для создания пироэлектрических чувствительных температурных детекторов. Таким образом, как видно, тройные ОСП могут использоваться при производстве самых разнообразных электронных и оптических устройств и приборов, благодаря их уникальным свойствам. Знание электронной структуры материала позволяет определить и спрогнозировать физические свойства керамики и кристаллов созданной из данного материала [1,2]. Ранее нами было проведено исследование электронной структуры тройных оксидов семейства перовскита [5].

В этой работе в рамках простой модели была определена зависимость ширины запрещенной зоны от разности ε_B´ - ε_O для керамик в упорядоченной фазе и кристаллов со структурой типа  и .

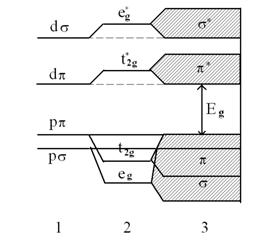
Рисунок 1. Электронное строение кубических ОСП типа АВО₃

1. энергии атомных уровней
2. уровни энергии в кластере ВО₆
3. энергетические зоны в кристалле ОСП типа АВО₃

Как видно из рисунка 1 ширина запрещенной зоны увеличивается с увеличением разности ε_B´ - ε_O и видно, что ширина запрещенной зоны в тройных ОСП больше чем, в ОСП типа АВО₃ с тем же самым атомом В. Результаты данной работы были получены в рамках простой модели [6], созданной Вольфрамом и Эллиалтиоглу. Эта модель - простая модель сильной связи, в которой используется базис из четырнадцати атомных орбиталей на элементарную ячейку для кубических ОСП с химической формулой АВО₃. Это пять d-орбиталей переходного элемента В и девять 2р-орбиталей трех ионов кислорода. Предполагается, что состояния щелочного или щелечноземельного атома А имеют энергию, значительно большую энергии состояний атомов В и О и практически не принимают участия в формировании валентной полосы и полосы проводимости. Таким образом, ион А является просто донором электронов для подрешетки ВО₃.

d-уровни иона В в октаэдрическом окружении атомов кислорода расщепляются на t_2g и е_g уровни, а р-уровни атомов кислорода в аксиальном окружении атомов атомов В - на рp и рs-уровни.

Рисунок 2 (а). Электронное строение кубических ОСП типа АВО₃

1. энергии атомных уровней
2. уровни энергии в кластере ВО₆
3. энергетические зоны в кристалле ОСП типа АВО₃

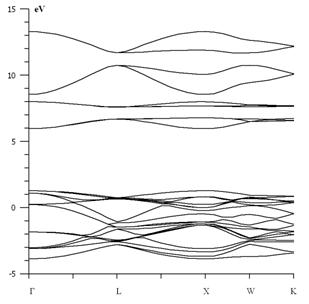
Рисунок 2 (б). Электронное строение кристалла в aYb_1/2 Ta_1/2 O₃

Три d-орбитали t_2g-симметрии (d_xy, d_xz, d_yz) взаимодействуют с рπ-орбиталями кислорода формируя π-зоны: по три эквивалентных зоны проводимости, валентных зоны и несвязующих уровня, лежащих у потолка валентной зоны. Две d-орбитали e_g-симметрии взаимодействуют с тремя рσ-орбиталями, образуя по две неэквивалентные σ-зоны проводимости, две валентные зоны и один несвязующий уровень, лежащий у потолка валентной зоны. Это даёт возможность электронный гамильтониан факторизовать на p и σ-блоки [6]. Из анализа аналитических результатов модели Вольфрама и выполненных ранее расчетов [3,4] найдено, что σ-зоны проводимости расположены существенно выше по энергиям, чем π-зоны проводимости.

Вершина валентной зоны формируется из несвязующих уровней. Эти состояния конструируются только из 2рО-орбиталей. Таким образом, в этой схеме наименьшая энергия возбуждения электронов (т.е ширина запрещенной зоны) полагается равной разнице между 2р - несвязующими состояниями, расположенными на вершине валентной зоны, и π-зоной проводимости.

На рисунке 2 нарисована качественная схема электронной структуры ABO₃ перовскитов. Электронная структура этой подрешётки представлена двумя группами π и σ-зон разделенных запрещенной зоной. Заполненные валентные зоны лежат под запрещенной зоной в то время, как пустые зоны проводимости выше зоны.

Точный теоретический анализ расчётов зонной структуры [6] показал, что дисперсия энергии в π-зонах может быть интерполирована моделью сильной связи с достаточной достоверностью, если включить в расчёт только рdπ-взаимодействия между В ионом и окружающими его ионами кислорода. d-d взаимодействием можно пренебречь, в то время как p-p взаимодействие важно только для описания дисперсии в 2p несвязующих зонах и может быть учтено в гамильтониане, как возмущение и приводит лишь к уширению несвязующих уровней у вершины валентной зоны [6]. Взаимодействие между 2sO-орбиталями и dB-состояниями смещает σ-зоны к большей энергии, но не влияет на π-зоны.

В рамках данной модели и были получены результаты в работе [5] (см. рис.1). Действительно, данная модель дает довольно точную картину электронного строения ОСП типа  в наиболее важной части, определении ширины запрещенной зоны. Однако можно ли применять данную модель и к тройным ОСП для определения у этих кристаллов ширины запрещенной зоны? Нет, никаких оснований полагать, что её нельзя использовать, но так же нельзя привести веских аргументов и в пользу того, что ею можно пользоваться.

Для ответа на этот вопрос нами был проведен расчет электронной структуры тройных ОСП с помощью метода сильной связи, в котором используется базис из 28 атомных орбиталей на элементарную ячейку. Это десять d-орбиталей переходного элемента В и В´ и восемнадцать 2р-орбиталей шести ионов кислорода.

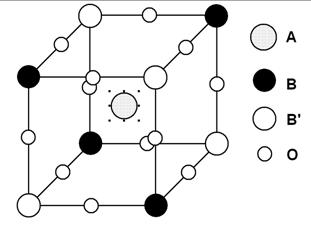
Рисунок 3. Упорядоченная фаза кристалла в aYb_1/2 Ta_1/2 O₃

Волновая функция в методе сильной связи представляется в виде суперпозиции атомных волновых функций:

(1)

где τ - номер зоны; k - квазиимпульс электрона; - радиус-вектор n-ой ячейки и j-го атома в ячейке соответственно; N - число ячеек в основной области кристалла; a =(nlm) - набор квантовых чисел атомного состояния  - ортогонализованные волновые функции атомов.

Энергию электронов можно разбить на две части - одночастичную и двухчастичную. Одночастичная часть энергии имеет вид:

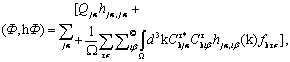(2)

где

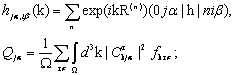            (3)

Ω- объем зоны Бриллюэна;  - число заполнения электронного состояния с номером τ и с проекцией спинового момента σ, равное единице или нулю в зависимости от того, заполнено это состояние или нет; Q_ia - заряд вносимый орбиталью с номером i на α-й атомный центр; Ф - многоэлектронная волновая функция, представленная в виде определителя, составленного из функций (1); штрих в (2) обозначает ограничение суммирования по состояниям ближайших друг к другу атомов.

Минимизация функционала энергии в выбранном классе функций (1) при условии ортонормированности набора атомных орбиталей приводит к системе линейных уравнений для .

              (4)

где

                        (5)

где штрих в (5) и (6) также, как и ранее, обозначает ограничение суммирования по состояниям ближайших друг к другу атомов. Система уравнений (1) решалась численно, в результате, был проведен расчет электронного строения кристалла BaYb_1/2Ta_1/2O₃ в упорядоченной фазе.

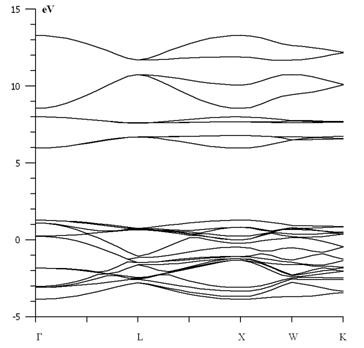
Рисунок 4. Электронное строение кристалла в aYb_1/2 Ta_1/2 O₃

Результаты расчетов находятся в хорошем согласии с экспериментальными результатами по определению ширины запрещенной зоны в тройных оксидах семейства перовскита [5], что подтверждает правильность выбора модели в работе [5].

СПИСОК ЛИТЕРАТУРЫ

1. Просандеев С.А. Электронное строение и физические свойства ионно-ковалентных кристаллов. //Ростов-н/Д. Изд. РГУ. 1990. 188с
2. Харрисон У. Электронная структура и свойства твердых тел. //Москва. Мир. 1983. в двух томах, Т.1. 381с. Т.2. 332с.
3. Маttheiss L.F. //Phys. Rev. B 1970. V.2. No.10. p.3918.
4. Michel-Calendini F.M. and Mesnard M.G. //Phys. stat. solidi (b) 1971. V.44. No.2. p. 117.
5. Raevski I.P., Prosandeev S.A., Osipenko I.A. //Phys. stat. sol. (b) 1996. V.198. p.695.
6. Wolfram T., Ellialtioglu S. //Phys. Rev. B. 1982. V.25. No.4. p.2697-2714.

Библиографическая ссылка