Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Файлы

Калмыков И.А., Хайватов А.Б., Сагдеев А.К.

Статья в формате PDF

118 KB

Проблема исследований: Одним из наиболее перспективных направлений обеспечения устойчивости к отказам является применение корректирующих кодов, обладающих свойством арифметичности. Использование полиномиальной системы классов вычетов (ПСКВ) позволяет обнаруживать и корректировать ошибки в процессе функционирования непозиционного спецпроцессора (СП). Разработка новых методов обнаружения и исправления ошибок в кодах ПСКВ, базирующихся на вычислении синдрома ошибки, позволит повысить эффективность функционирования СП класса вычетов.

Решение проблемы: Повышенные требования к качеству решения задач, например цифровой обработки сигналов, предопределили новый этап в развитии математических моделей, обеспечивающих параллельную обработку. Среди таких систем особое место занимает полиномиальная система классов вычетов (ПСКВ), которая относится к параллельным вычислительным системам. В данной алгебраической системе, входные отсчеты , представленные в полиномиальной форме, приводятся к виду

,                           (1)

где , .

Наряду с высоким быстродействием, обусловленным малоразрядностью остатков и модульностью вычислений, полиномиальная система классов вычетов обладает способностью обеспечивать устойчивость к отказам вычислительным системам, функционирующим в ПСКВ [1].

Среди методов обнаружения и коррекции ошибок в модулярных кодах особое место занимает метод, базирующийся на вычислении синдрома ошибок по контрольным основаниям [1,2]. В основу данного метода положено определение разности между значениями остатков  по контрольным основаниям полинома  и результатом вычисления остатков 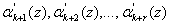  с использованием рабочих оснований. Математически данный метод можно представить:

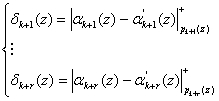                     (2)

где ;

f - алгоритм вычисления остатков по рабочим основаниям.

В работе [1] представлен метод расширения системы оснований ПСКВ, а так же структура устройства, реализующего (2) в расширенном поле Галуа GF(2⁴). Основным достоинством данного метода является возможность организации параллельных вычислений с использованием нейронной сети (НС) прямого распространения.

В работе [3] представлено устройство, реализованное в нейросетевом базисе, осуществляющее процедуру поиска и исправления ошибок на основе расширения системы оснований.

Устройство функционирует следующим образом. На вход устройства для обнаружения и исправления ошибок в ПСКВ подается контролируемое число, представленное в полиномиальной форме:

A(z)=(α₁(z), α₂(z),..., α_k(z), α_k+1(z), α_k+2(z)).                      (3)

Данный вектор A(z)=(α₁(z), α₂(z),..., α_k(z), α_k+1(z), α_k+2(z)) записывается в регистр хранения. На вход первого блока вычисления синдрома подается

A¹(z)=(α₁(z), α₂(z),..., α_k(z), α_k+1(z))                   (4)

c образованием на его выходе сигнала:

δ₁(z)=(α_k+1(z)+α^*_k+1(z))mod р_k+1(z).                  (5)

При этом:

α^*_k+1(z)=λ⁽¹⁾₁α₁(z)+ λ⁽¹⁾₂α₂(z)+...+ λ⁽¹⁾_kα_k (z),                  (6)

где λ⁽¹⁾_i - константы системы ПСКВ.

Одновременно с этим на входы второго блока вычисления синдрома с выходов регистра подается

A²(z)=(α₁(z), α₂(z),..., α_k(z), α_k+2(z)),                  (7)

С образованием на выходе сигнала:

δ₂(z)=(α _k+2(z)+ α ^*_k+2(z))mod p_k+2(z).                               (8)

При этом:

α^*_k+2(z)= λ⁽²⁾₁α₁(z)+ λ⁽²⁾₂α₂(z)+...+ λ⁽²⁾_kα_k (z),                 (9)

где λ⁽²⁾_i - константы системы.

Величины δ₁(z) и δ₂ (z) в двоичном виде поступают на входы блока памяти и выбирают оттуда соответствующую константу ошибки. Эта константа ошибки поступает в сумматор, где суммируется с искаженным A(z), представленном в непозиционном виде. Исправленное представление A(z) с выхода сумматора подается на выход устройства.

Выводы: Применение методов вычисления синдрома ошибки, базирующихся на расширении системы оснований ПСКВ, позволяет обеспечивать Надежную работу высокоскоростных параллельных вычислительных устройств в реальном масштабе времени.

СПИСОК ЛИТЕРАТУРЫ

1. Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
2. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа/Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68с.
3. Калмыков И.А., Хайватов А.Б., Никульников А.С. Устройство для обнаружения и исправления ошибок в полиномиальной системе класса вычетов. Решение о выдаче патента (№ 2004102274/09(002159). Приоритет от 26.01.2004. Бюл. №19 (II). с.568-569.

Библиографическая ссылка