Сложную систему практически невозможно описать полно и детально, что вытекает из самого определения такой системы. Основная дилемма состоит в нахождении компромисса между простотой описания, что является одной из предпосылок понимания, и необходимостью учета многочисленных поведенческих характеристик сложной системы.
Система задается семейством моделей, каждая из которых описывает поведение системы с точки зрения различных уровней абстрагирования. Для каждого уровня существует ряд характерных особенностей и переменных, законов и принципов, с помощью которых и описывается поведение системы. Построение такой системы моделей должно базироваться на ряде принципов, обеспечивающих корректность и достоверность результатов моделирования [ 1].
Анализ принципов построения системы математических моделей структурно-сложных объектов и принципов иерархического многоуровневого моделирования позволит предложить методику построения многослойного стратифицированного описания сложной системы в условиях неопределенности, что дает возможность объединить отдельные модели и разрозненную информацию о системе на единой методологической основе [2].
На каждом уровне ![]() описания предметной области имеется свой набор входных
описания предметной области имеется свой набор входных ![]() и выходных переменных
и выходных переменных ![]() . Каждый уровень описания характеризуется для упрощения только одной моделью уi = Fi (xi). Каждому параметру на вышестоящем уровне соответствует определенный набор параметров нижестоящего или базового уровня:
. Каждый уровень описания характеризуется для упрощения только одной моделью уi = Fi (xi). Каждому параметру на вышестоящем уровне соответствует определенный набор параметров нижестоящего или базового уровня:
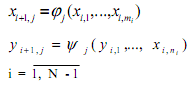
Некоторые параметры описания предметной области могут непосредственно измеряться как на базовом уровне, так и на вышестоящих уровнях описания. Однако погрешности измерений, отсутствие ряда замеров и неполнота информации по используемым моделям приводят к тому, что решения, получаемые на разных уровнях, не соответствуют друг другу в смысле выполнения соотношений (1).
Исходные данныеДопустимость решений по моделям задается нечетким множеством M⊂Y, измерения характеризуются нечетким ограничением Z⊂Y и скоординированность - нечетким множеством K⊂Y. Тогда нечеткое подмножество D - M∩Z∩K называют нечетким решением.
Основная особенность координации решений в многоуровневой иерархической системе заключается в том, что решение нижестоящего уровня зависит от выбора со стороны вышестоящего уровня, а решение вышестоящего уровня, в свою очередь, зависит от отклика элементов нижестоящего уровня. Это дает возможность сократить обмен информацией между уровнями и обеспечить локальную обработку информации по отдельным моделям. На основе этого принципа построена рекуррентная процедура принятия решений, которая состоит из нескольких этапов [3].
Разработаные численные методы «мягких» вычислений для координации многоуровневых модельных ограничений, которые позволяют уменьшить неопределенность и скорректировать функции принадлежности входных данных таким образом, чтобы они соответствовали согласованным решениям на верхних уровнях описания системы. Предложено два численных метода нахождения системных решений: коррекция по носителю нечеткого множества решений и коррекция по его a-уровням. Отдельно рассматривается случай, когда и функции принадлежности для нижележащих уровней заданы дискретно по a-уровням.
Предлагаемый подход отвечает основным требованиям системного анализа, так как обеспечивает при моделировании целостность рассмотрения сложной системы за счет согласования различных уровней абстрагирования на основе теории нечетких множеств, позволяющего целиком удерживать в поле зрения всю систему в целом для решения задачи на всех уровнях обобщения; всесторонность рассмотрения системы на основе учета моделей разных уровней описания и связей между ними.
СПИСОК ЛИТЕРАТУРЫ:
- Колесов Ю.Б., Сениченков Ю.Б. Модели-рование систем. Динамические и гибридные системы. - СПб.: BHV-Санкт-Петербург. - 432 с.
Библиографическая ссылка
Морозов С.А., Манжула В.Г., Федосеев СВ. ПРИНЦИПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СЛОЖНЫХ СИСТЕМ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ // Фундаментальные исследования. 2009. № 4. С. 74-75;URL: https://fundamental-research.ru/ru/article/view?id=4468 (дата обращения: 26.01.2026).



