Введение
В настоящее время много работ сосредоточено на создании разнообразных биржевых систем принятия решений, лежащих в основе как систем поддержки принятия решений, так и в алгоритмах торговых ботов. Задачей торгового бота является обработка временного ряда динамики цены и определение точки открытия позиции, точки закрытия позиций, зоны поддержки инвестиционных позиций. Детальное исследование этих методик представлено в [1]. На рис. 1 приведен пример функционирования торгового бота и генерации различного рода торговых сигналов, для валютной пары EUR / USD.
Подобный принцип заложен в множестве аналогичных механических торговых систем, лежащих в основе торговых ботов, принципы которых описаны в работе [1] и реализованы в работах автора [2, 3].
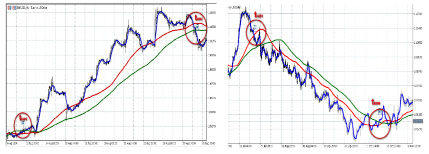
Рис. 1. График цен EUR/USD, с частотой дискретизации в 1 час (баровый график), с тремя скользящими средними, рассчитанных по ценам закрытия за 14 (синяя), 75 (красная) и 127 (зеленая) периодов
Каждый подобный бот может использоваться как отдельно, так и в совокупности с другими ботами. Каждый бот обладает достоинствами и недостатками и может быть адаптирован к исключительным и специфическим рыночным условиям.
Инвестиционный риск зависит от самой позиции, ее объема, применяемого бота. Он отражает степень вероятности, с которой инвестор оценивает различные сценарии развития рыночной динамики. В конечном итоге при таком подходе оценки инвестиционного риска управления целесообразно оценивать не риск актива, а риск торгового бота.
Алгоритм бота можно охарактеризовать некоторыми возможностями для оценки целесообразности открытия «коротких» или «длинных» позиций, в чем проявляется его способность оценивать вероятные рыночные изменения. Эмпирическое исследование работы данного алгоритма будет давать определенные результаты, которые могут быть оценены с точки зрения его эффективности (доходности). Однако имея достаточно большой запас исторических данных, динамики того или иного актива, используя определенное программное обеспечение, либо собственные программные разработки, имеется возможность проведения моделирования процесса работы данного алгоритма на прошлых данных. Полученные данные позволяют оценивать доходность и риск того или иного бота.
Данная методика должна предусматривать:
‒ разработку методики для создания и анализа набора ботов (алгоритмов управления капиталом), а также формализация этой задачи на математическом уровне;
‒ определение исходных данных задачи оптимизации набора ботов;
‒ определение ограничения задачи оптимизации набора ботов;
‒ определение целевых показателей оценки доходности и риска набора ботов;
‒ подбор оптимальных ботов для обеспечения диверсификации.
Цель исследования – разработка подходов к оценке доходности и риска биржевых торговых ботов, подходов к распределению капитала между ботами для обеспечения снижения рисков управления капиталом.
Материалы и методы исследования
В процессе исследования использовались статистический и системный анализ, методы моделирования.
Для поиска оптимальных решений поставленной задачи использовались методы искусственного интеллекта, такие как генетические алгоритмы.
Данными для исследования являются ценовая динамика валютных пар EUR/USD из открытых источников рынка forex.
Результаты исследования и их обсуждение
Определив основные постулаты подхода по распределению капитала по разным торговым ботам, приступим к формализации данной задачи. Для начала определим исходные данные, которыми располагает автор, для их обработки – в первую очередь это цена актива c[t], характеризующаяся дискретностью во времени.
Имея начальный инвестиционный капитал К в некоторый момент времени, а также располагая множеством (Δ) доступных торговых ботов, каждый из которых генерирует поток позиций (решений) φ, произведем оценку ожидаемой доходности данных решений, на определенном интервале времени от tκ до tH и рассчитаем по формуле
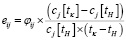 , (1)
, (1)
где φij – j-инвестиционное решение (позиция) i-бота, принимающее значение из множества {-1;0;+1}, соответствующие «короткой», «нулевой» и «длинной» позиции соответственно,
(tκ – tH,) – временной интервал между принятием решения и его отменой,
cj[tH] – значение цены в начальный момент времени,
cj[tκ] – значение цены в конечный момент.
Оценка доходности бота определяется по формуле
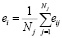 , (2)
, (2)
где Nj – количество сделок, проведенное bi.
Оценка доходности торгового бота определяется путем моделирования. Инструментом подобной оценки могут выступать такие программные продукты, как Equis MetaStock Professional 7.0 или Omega Research TradeStation 2000i. Торговые боты, оценка ожидаемой доходности которых меньше или равна нулю, не рассматриваются. Подобная оценка может быть проведена только программным путем, что обосновывает в дальнейшем использование генетических алгоритмов для проведения оптимизации набора торговых ботов.
Инвестору может быть доступно некоторое число торговых ботов (Δ), используя которые осуществляется управление некоторым объемом денежных средств К. Обозначим это множеством B, состоящим из отдельных ботов bi.
Процедура оценки характеристик набора ботов (B), заключающаяся в нахождении показателей ожидаемой доходности Ebi и риска Vbi каждого отдельного торгового бота bi. Оценить показатели доходности и риска отдельного бота возможно только эмпирически, используя моделирование применения i-го бота bi, на исторических данных динамики рискового актива, выраженной в изменениях капитала К, под действием бота bi. В качестве показателя, оценивающего доходность отдельного торгового бота, используется математическое ожидание доходности бота, рассчитанное по формуле (2). Ожидаемый риск торгового бота можно оценить дисперсией, рассчитанной по формуле
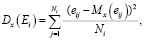 (3)
(3)
где eij – оценка ожидаемой доходности j сделки, проведенной i-м торговым ботом,
Ni – количество принятых решений при использовании i-го торгового бота.
Боты, имеющие отрицательную ожидаемую доходность, исключаются из множества B. Тем не менее использование дисперсии в качестве метрики для оценки риска bi не является адекватным, поскольку, применительно к изменению капитала K, стандартное отклонение отражает средний уровень как положительных, так и отрицательных изменений величины K. В то время как подлинный риск, который воспринимает управляющий (инвестор), связан исключительно с возможными отрицательными колебаниями.
Применение величин, так или иначе характеризующих «среднее» значение отрицательных отклонений, также не является правильным решением, поскольку даже при средних показателях существует риск крупных одноразовых убытков.
К примеру, если за год средний убыток вклада K составил 10 %, то в начале этого периода могло быть зафиксировано падение на 65 %, а далее варьироваться в пределах 1–3 %, и размер капитала K оставался неизменным до завершения года, тем не менее это привело к потере инвестором или управляющим половины изначально вложенных средств.
Автор предлагает оценивать риск исходя из закона плотности распределения вероятности. Используя оценку плотности распределения вероятности изменения показателя доходности торгового бота, введем показатель VR, при котором вероятность события отклонения ei от данной величины VR, будет равняться заданному порогу (1 – α), что соответствует выражению
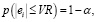 (4)
(4)
где α – порог вероятности.
В случае непрерывной случайной величины это можно было бы записать следующим образом, формулой
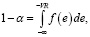 (5)
(5)
где f(e) – функция плотности распределения вероятности.
В рассматриваемом случае имеются дискретные случайные величины, и закон плотности распределения оценивается методом моделирования [4]. В случае получения нормально распределенной случайной величины нахождение VR осуществляется по формуле (6), сводится к поиску квантиля z1–α:
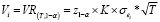 , (6)
, (6)
где σei – среднеквадратическое отклонение случайной величины ei.
В контексте дискретного характера случайной величины целесообразно производить оценку плотности распределения данной величины.
Ввиду стохастической природы показателей эффективности алгоритмов, на основании которой функционируют торговые боты, существует вариативность и нестабильность результатов их практического применения. В этой связи более рациональным подходом является использование комплексного набора торговых ботов, то есть формирование агрегированного набора B из отдельных ботов bi, что способствует повышению надежности и устойчивости торговых результатов. Совокупная эффективность управляемого набором ботов B, капитала K, в этом случае, будет определяться как
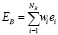 , (7)
, (7)
где NB – количество ботов в наборе B,
wi – доля капитала приходящегося на bi, wi > 0.
Перейдем к оценке совокупного показателя риска набора ботов. Диверсификация риска в рассматриваемом случае заключается в стремлении сформировать набор независимых друг от друга торговых ботов bi, что будет компенсировать недостатки одного b1 другим ботом b2.
В процессе выбора независимых между собой торговых ботов bi оценим попарную корреляцию между ними. Целью является выявление таких сочетаний, при которых общий коэффициент корреляции, вычисляемый согласно формуле (8), стремится к нулю в идеальном случае:
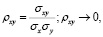 (8)
(8)
где σxy – ковариация доходности двух выбранных ботов.
Отбор некоего множества независимых ботов из множества B, при условии положительного математического ожидания доходности, в теории открывает путь к решению задачи стабилизации показателей эффективности управления набором ботов. Это дает возможность эффективно направлять финансовые средства K, при условии бесконечного увеличения количества инвестиционных инструментов B, несмотря на возможность убыточности отдельного бота.
Оценка риска набора bi характеризуется показателем дисперсии кривой K и оценивается формулой
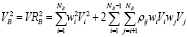 , (9)
, (9)
упрощая которую, исходя из вышеизложенных формул, получаем выражение
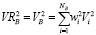 . (10)
. (10)
Формализовав подходы к оценке доходности и риска рассматриваемого набора ботов и установив ограничения, перейдем к построению оптимизационной модели, сформулированной выражением
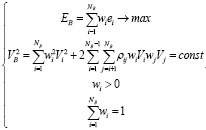 (11)
(11)
Для решения задачи (11) автором использован генетический алгоритм.
В рамках научного исследования, представленного в одной из работ автора, формализован генетический алгоритм [2]. Однако генетические алгоритмы требуют индивидуальной формализации для каждой из решаемых задач, чтобы адаптировать алгоритмические алгоритмы к уникальным ограничениям в постановке задач оптимизации.
Генетический алгоритм оперирует следующими понятиями:
1) Oi – множество особей, представляющих собой потенциальные решения задачи;
2) Si – множество наборов хромосом, представлений потенциальных решений, которыми оперирует генетический алгоритм;
3) функция кодирования c(o);
4) функция декодирования c-1(o);
5) функция оценки приспособленности особи f:O→R, такая, что если f (o1) > f (o2), то o1 считается решением лучше, чем o2, R – множество вещественных чисел;
6) функция оценки приспособленности представления φ:S→R;
7) ограничения, поставленные в задаче (11).
Генетический алгоритм производит операции с представлениями особей. Для поставленной задачи особью является вектор весов
{w1, w2,… wNb},
где wi – вес i-го метода в j-м наборе.
Двоичным представлением в данном случае будет вектор
{x1, x2,… xNb}
где xi –двоичное представление wi.
На каждой итерации генетический алгоритм обрабатывает некоторое множество допустимых решений (популяция) [5]. Популяция P(t) является множеством двоичных представлений допустимых решений задачи (11), представленного выражением
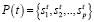 , (12)
, (12)
где p – целое число, определяющее размер популяции,
t – номер поколения.
Генетический алгоритм моделирует эволюционные процессы [6], в результате которых происходит рост функции приспособленности как отдельных особей, так и популяции в целом [7]. Если в момент t имеется популяция P(t), состоящая из p-особей, то она может характеризоваться следующими показателями:
1) средней приспособленностью особей в популяции;
2) минимальным и максимальным значением приспособленности особи в популяции;
3) другими величинами, исходя из необходимости.
Моделирование эволюции заключается в смене поколений, то есть переходе от популяции P(t) к популяции P(t+1) с разной степенью обновления популяции (допустимы варианты неперекрывающейся или перекрывающейся популяции). Начальная популяция особей формируется случайным образом. Оценка уровня приспособленности особей производится исходя из вида целевой функции, указанной в задаче (11), которая оценивается формулой
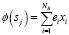 , (13)
, (13)
где xi – вес,
ei – ожидаемая доходность i-го бота.
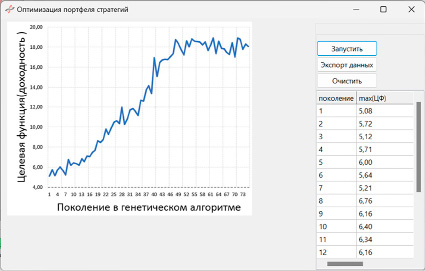
Рис. 2. Результаты моделирования поиска генетическим алгоритмом и динамика целевой функции
В результате выполнения этой операции получаем числовые показатели, которые отражают уровень приспособленности каждой особи в популяции [8]. Каждое сгенерированное или полученное в результате генетических операторов потенциальное решение, подлежит тщательной проверке на соответствие установленным критериям и ограничениям задачи (11).
Модификация алгоритма обосновывается поставленной задачей, так как полученные в результате кроссовера особи могут не удовлетворять условиям допустимости, накладываемые решаемой задачей. Обычно они подлежат уничтожению, что затрачивает ресурсы на работу алгоритма и увеличивает время его сходимости [9]. Для нивелирования этих проблем автор использует оператор нормирования полученных хромосом, приводящих их к допустимому виду и сохраняющих эквивалентность решения. Предложенная версия генетического алгоритма описана в работе [10, 2] и прошла апробацию, показав эффективность при подборе порядков скользящих средних [2].
Заключение
Для исследования предложенной модели были выбраны торговые боты, использующие скользящие средние, фильтры Баттерворта и бот, использующий индикатор «Stochastic» из работы [1]. Основные постулаты эмпирической оценки качества генетических алгоритмов рассмотрены автором в работе, для проведения вычислительного эксперимента разработана программная модель генетического алгоритма. Основным показателем эффективности работы генетических алгоритмов является динамика функции приспособленности, которая представлена на рис. 2.
Рассмотрены алгоритмы оценки показателей, характеризующих доходность и риски торговых биржевых ботов. Научная новизна заключается в предложенной постановке задачи распределения капитала по нескольким торговым ботам, позволяющей разделить риски, и адаптации данной задачи под решение модифицированным генетическим алгоритмом.
Таким образом, представленная работа вносит существенный вклад в понимание процессов управления капиталом и, в частности, в процессы параметрической оптимизации автоматизированных стратегий принятия решений. В результате исследования предлагаются вполне понятные инструменты, позволяющие существенно улучшить результативность процессов инвестирования в биржевые рисковые активы.
Библиографическая ссылка
Портнов К.В. ПРАКТИЧЕСКИЕ АСПЕКТЫ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ В ЗАДАЧАХ УПРАВЛЕНИЯ ТОРГОВЫМИ БОТАМИ // Фундаментальные исследования. 2024. № 12. С. 101-106;URL: https://fundamental-research.ru/ru/article/view?id=43747 (дата обращения: 20.02.2026).
DOI: https://doi.org/10.17513/fr.43747



