В настоящее время сети подвижной радиосвязи (СПРС) бурно развиваются. Быстро растет спрос мобильных абонентов в мультимедийных услугах, таких как мобильный доступ в Internet, передача видеоизображений, асимметричные и интерактивные услуги широкополосной связи и так далее. Ожидается значительное повышение объема интегрального трафика в СПРС третьего поколения. Поэтому особую актуальность приобретает проблема разработки метода анализа пропускной способности системы подвижной радиосвязи (СПРС) в совмещенном режиме передачи речи и данных.. Теория телетрафика использует при построении моделей аппарат и методы, развитые в теории массового обслуживания. К сожалению, большинство этих моделей и методов применимы только для весьма узкого класса ситуаций с простейшими предположениями о характере входного потока, дисциплине и распределении времени обслуживания. Проблемы, возникающие в современных системах связи, не могут анализироваться этими методами в точной обстановке. По этой причине единственным реальным средством получения численных значений характеристик качества функционирования систем связи является использование метода декомпозиции, когда построенная модель с помощью упрощающих преобразований разбивается на отдельные модули, каждый из которых анализируется независимо с использованием стандартных средств теории телетрафика.
Предполагается, что в систему поступают два потока: речь и данные с соответствующими интенсивностями, l1 - интенсивность поступления пуассоновского потока речевой нагрузки; l2 - интенсивность поступления пуассоновского потока пакетов данных; m - параметр экспоненциального распределения времени передачи речевого сообщения. Речевое сообщение имеет абсолютный приоритет в получении каналов связи перед пакетом данных и так же, как пакет, использует для своей передачи единственный канал связи.
Для примера рассмотрим подсистему базовых станций сотовой связи стандарта GSM/GPRS(BSS). В состав BSS входит контроллер базовых станций BSC, который обслуживает потоки речи и данных, т.е. одной из его основных функций является управление распределением канального ресурса для поступающей нагрузки. В системе предполагается режим равного доступа любого из М абонентов к любому из L предоставляемых каналов. Каждый абонент системы имеет возможность передавать пакеты данных или речевые вызовы. Пакеты данных могут предназначаться для передачи только по освободившимся в данный момент каналам из общего числа Lканалов. Из теории телетрафика известно, что среднее время обслуживания Пуассоновского потока требований Tср =1/m, поэтому будем считать, что все пакеты имеют одинаковую длину, равную b=1/m. Соответственно нагрузка пакетной передачи данных определяется 
, а речевая нагрузка 
. В данном случае передача пакетов осуществляется по l освободившимся каналам, то есть каждый абонент получает «случайный доступ» в один из l освободившихся каналов.
В силу независимости процесса передачи речевых сообщений от процесса поступления и обслуживания пакетов данных оценку значений N 1 и Lср можно вести в рамках стандартной модели теории телетрафика с потерями заблокированных вызовов, имеющей L полнодоступных каналов, Пуассоновский входной поток нагрузки интенсивности l1, экспоненциально распределённое время обслуживания со средним 1/m. Доля сообщений речевой нагрузки, потерянных из-за отсутствия свободных для передачи каналов N 1 определяется вследствие пуассоновского характера поступления речевых сообщений формулой Эрланга В.
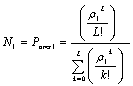(1)
Из теории телетрафика известно, что среднее число каналов, свободных от обслуживания речевых вызовов, т.е. каналов, пригодных для передачи пакетов 
=L-r1(1-Pотк1 ).
Так как процесс передачи пакетов зависит от процесса поступления и обслуживания речевых сообщений оценку значений можно вести в рамках стандартной модели теории телетрафика с потерями заблокированных вызовов, имеющей полнодоступных каналов, Пуассоновский входной поток нагрузки интенсивности l2, длиной пакета 1/m.
Подставив эту выражение в формулу Эрланга В получим искомое N 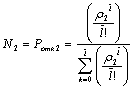2
(2)
Среднее число каналов системы, занятых передачей речевых сообщений, Lср и пакетов данных 
определяются как соответствующие средние значения:
(3)
Алгоритм оценки доли успешно переданных пакетов и времени их пребывания в системе основан на том, что доля потерянных речевых сообщений достаточно мала. Построим вспомогательную модель, объединив в исходной модели поступающие потоки речевых сообщений и пакетов данных в один поток пакетов. Понятно, что доля потерянных пакетов и среднее время пребывания пакета в системе на передаче, посчитанные для вспомогательной модели, будут верхними оценками для соответствующих характеристик исходной модели. Это так, поскольку во вспомогательной модели пакет, являющийся аналогом заблокированного и, следовательно, потерянного в исходной модели речевого сообщения, теперь становится в очередь на повторную передачу с некоторой задержкой. Таким образом, во вспомогательной модели передается больший по сравнению с исходной моделью объем нагрузки, обеспечивая верхний характер соответствующих оценок. Найденные оценки доли потерянных пакетов и среднего времени пребывания пакета в системе на передаче, будут близки к их истинным значениям в силу достигнутой на первом этапе расчетов степени малости потерь речевых сообщений.
Схема функционирования модели, используемой для оценки характеристик пакетов данных, выглядит следующим образом. У нас имеется система связи с L полнодоступными каналами, на которую поступает пуассоновский поток пакетов данных интенсивности l1+l2 . Время передачи пакета имеют одинаковую длину, равную 1/m,. Если все имеющиеся L каналов системы заняты, то пакет через некоторое время предпринимает попытку повторной передачи.
Доля пакетов данных, получивших отказ из-за занятости всех каналов системы, оценивается величиной 
, которая вследствие пуассоновского характера поступления пакетов определяется как доля времени пребывания упрощенной модели в состоянии, когда в системе находятся L пакетов на обслуживании
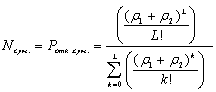. (4)
Доля пакетов данных, потерянных из-за прерывания их передачи по каналу поступившим приоритетным речевым сообщением, Nпрер. оценивается как отношение интенсивностей соответствующих событий в упрощенной модели
(5)
Значение общей доли потерянных пакетов данных 
оценивается как сумма долей пакетов, потерянных по указанным выше причинам,
. (6)
Доля успешно доставленных пакетов данных Nусп. оценивается как величина, дополнительная к 
. (7)
Среднее число каналов анализируемой модели системы подвижной радиосвязи, занятых на передачу пакетов данных, 
определяется как соответствующее среднее значение:
(8)
Среднее время пребывания пакета на передаче Tпреб. находится по формуле Литтла
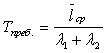
Для того чтобы выяснить возможно ли предложенную выше методику использовать при проектировании реальных СПР была разработана программа имитационного моделирования. В данном случае имитационное моделирование применяется для оценки погрешности, возникающей при использовании расчетных моделей вместо точных.
Окончательно утверждать о справедливости применения разработанной модели для систем подвижной радиосвязи можно только после анализа совпадения выборочной оценки плотности, или гистограммы, полученной в ходе реализаций программы имитационного моделирования с расчетной формой. В рамках математической статистики для этого широко используют критерий согласия Неймана-Пирсона.
Вектор гистограммы представляет собой 
, где 
, 
, 
- число испытаний, попавших в интервал с индексом ν. Вектор расчетных вероятностей формируется как 
, где 
, ,
-й интервал, 
- используемая параметрическая модель для плотности распределения анализируемой выборки наблюдений 
, 
- оценка максимального правдоподобия неизвестного параметра 
, выполненная по выборке 
Степень рассогласования гистограммы и расчетного вектора вероятностей в критерии Неймана-Пирсона
(9)
Суть цитируемой теоремы и критерия состоит в том, что при увеличении выборки 
и справедливости применяемой параметрической модели , распределение статистики Z(9) сходится к стандартному 
, где 
–число степеней свободы, s - размерность вектора параметров .
В данном случае L=12, s=4, N=100 и q= 7. По таблице телетрафика находим 5- %-ный уровень значимости 
и вычисляем 
. Так как это значение значительно меньше критического значения, то можно применять предложенную модель для анализа систем подвижной связи в совмещенном режиме.
Библиографическая ссылка
Шорин О.А., Бабин А.И., Иванов А.М. МОДЕЛЬ РАСЧЕТА ПРОПУСКНОЙ СПОСОБНОСТИ СИСТЕМЫ ПОДВИЖНОЙ РАДИОСВЯЗИ 3G В РЕЖИМЕ РЕЧЬ-ДАННЫЕ // Фундаментальные исследования. – 2007. – № 12-3. – С. 470-472;URL: https://fundamental-research.ru/ru/article/view?id=4373 (дата обращения: 23.11.2024).