Внутренние шумы высокочувствительной измерительной аппаратуры являются крайне не желательным явлением. Борьба с ними ведется на всех уровнях от проектирования до отработки технологии изготовления электронных схем. Большинство механизмов возникновения шумов известны и приемы подавления их уровня отработаны достаточно хорошо. Кроме одного загадочного шума, описываемого в литературе как l/f-шум. Загадочность данного явления заключается в следующем: 1) это явление имеет крайне широкое распространение в природе от шумов в полупроводниковых приборах, до употребления таблеток; 2) в формуле 1/f степень у имеет пределы от 0,8 до 1,2, что само по себе необычно для описания физических явлений; 3) природа возникновения данного шума до сих пор достоверно не установлена.
Отсутствие достоверной модели возникновения данного шума не позволяет эффективно бороться с вышеупомянутым явлением.
Предлагаемая в статье [1] барьерная модель возникновения l/f-шума хорошо согласуется с экспериментальными данными [2] и объясняет возникновение l/f-участков наличием потенциальных барьеров. Но, это явно не единственная модель. Т.к. она объясняет только одно из проявлений l/f-шума, а именно возникновение l/f-участков и почему у ряда исследователей [3] предел степени у справа стремился к 1.
Должна существовать как минимум еще одна модель. Т.к. во-первых, в классическом l/f-шуме пределы степени у от 0,8 до 1,2 [4,5], а во-вторых, в классическом l/f-шуме, нет обособленных l/f-участков и при у=0,8 и при у=1,2 кривая имеет классический 1/fy вид.
Одним из возможных механизмов генерации l/f-шума может быть пуассоновский процесс.
Рассмотрим пуассоновский процесс - частный случай счетного процесса, т.е. целочисленного процесса с единичными приращениями.
Процесс этого типа можно описать случайной последовательностью точек {4} вдоль временной оси
![]() (1)
(1)
где ω(t) - единичная функция включения ω(t) = 1/2(1+signt). Таким образом, случайное значение N(t) эквивалентно числу точек включения между 0 и t. Процесс может быть охарактеризован вероятностью события [N(t) = n] для каждого t≥0 и n=0, 1,2, ...
Формула спектральной плотности выше указанного процесса [6]
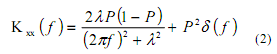
где P2δ(f) - постоянная составляющая при f=0;
Р - вероятность появления события (включений или появления импульса) в единичный интервал времени;
d(f) - дельта функция.
Величины, входящие в выражение (2) можно трактовать следующим образом. Р - вероятность появления 1 соответствует коэффициенту заполнения процесса, то есть отношению средней длительности импульса к среднему периоду процесса. Величина 1 характеризует среднюю частоту (интенсивность) процесса, a f - текущую частоту. Выражение (2) справедливо для относительного значения амплитуды импульсов, равного 1. Чтобы получить спектральную плотность средней мощности в обычной размерности В2/Гц, нужно умножить выражение (2) на квадрат средней амплитуды импульсов U2.
Выражение (2) является обобщением выражения c/fy на весь диапазон частот. При достаточно большой частоте (интенсивности) процесса 1, изменение текущей частоты в области низких частот мало влияет на значение спектральной плотности и ход кривой совершенно отличается от выражения 1/f Остается только выяснить, каково это соответствие для сверхнизких частот, для которых используется выражение c/fy. При малой частоте (интенсивности) процесса l<<f для сверхнизких частот, спектральная плотность начинает вести себя как c/fy Так уже при l=0,03 получается достаточно хорошее соответствие спектральной плотности и кривой c/fy при показателе степени у=0,8 (рис. 2).
Для определения предела слева значения степени у в эмпирической формуле c/fy , попробуем решить задачу подобную той, которую решают экспериментаторы, и подберем график c/fy к полученным результатам. Только вместо полученных эмпирическим путем данных будем использовать данные, которые были рассчитаны по приведенной выше методике. Расчеты будем вести при Р=0.5. При заданном значении частоты (интенсивности) процесса 1, найдем степень у соответствующую оптимальному совпадению графика c/fy с графиком рассчитанным по формуле (2). В данном случае график рис.1 по формуле (2) определен значением 1=0,03, у=0,8 и с=0,06.
Как видно из рис. 1 совмещение графиков достаточно хорошее, чтобы признать утверждение об идентичности графиков. Если же график c/fy «оторвать» от осей и передвигать как кривую, а именно так чаще всего и делают исследователи, подбирая график 1/f к экспериментальным кривым, то совпадение графиков будет очень хорошим.
Как видно из рис.1, предел слева степени у в эмпирической формуле c/fy равен 0,8. При частоте (интенсивности) процесса 1>0,03, даже при показателе степени у<0.8 уже не достичь достаточно хорошей аппроксимации.
Максимальное значение спектральной плотности Kxx(f) при f→0 соответствует выражению .
![]()
Так при Р=0,5,1=0,03 и U=1B KXX(0)=0,5U2/λ, = 16,7 В2/Гц. В отличие от этого, значение выражения c/fy всегда стремится к ¥ при f→0. Стремление энергетического спектра к ¥ при 1→0 объясняется тем, что при очень малой частоте (интенсивности) процесса, период Т=2р/1, а соответственно и длительность импульса tи, равная половине периода (при Р=0,5), стремится к бесконечности. При этом энергия сигнала, равная U2tи также стремится к бесконечности. При малой частоте (интенсивности) процесса и tи→0, P→0 и низкочастотная составляющая энергетического спектра становится малой величиной.
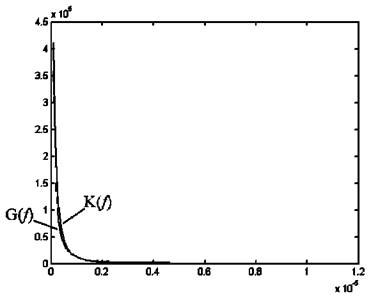
Рис.1. Совмещение графиков спектральной плотности по формуле (10) при Р=0,5; 1=0.03 и c/fy
при y=0,8 и c=0.06(G = 0,06/f0,8).
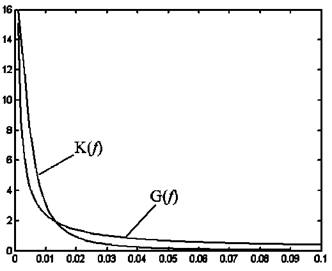
Рис. 2. Совмещение графиков спектральной плотности по формуле
(10) Р=0.5; 1=0.000001; с=0.000013; у=1.5
Вывод: 1) В случае аппроксимации l/f-шума пуассоновским процессом предел слева в эмпирической формуле c/fy действительно существует. 2) Согласно представленной модели предел степени у равен 0,8, что соответствует экспериментальным данным. 3) Данный предел равный 0,8 определен математикой процесса, формула (2).
При определении предела степени у справа, при Р=0,5 и 1=0,01 и меньше вид (кривизна) графика не меняется, меняется только размерность графика при этом у=1,2.
При дальнейшем уменьшении частоты (интенсивности) процесса (1=0,005 и меньше) показатель степени у увеличивается вплоть до величины у=1,5, и далее не меняется рис.2.
Как видно из рис.2 совмещение достаточно хорошее, чтобы считать утверждение о совпадение графиков обоснованным.
Вывод: 1) В случае апроксимации l/f-шума пуассоновским процессом предел справа в эмпирической формуле c/fy действительно существует, что соответствует экспериментальным данным. 2) Согласно представленной модели предел степени у равен 1,5, он несколько больше общепринятого предела 1,2, но в целом не противоречит экспериментальным данным. 3) Данный предел равный 1,5 определен математикой процесса, формула (2).
Выводы:
Констатируя выше приведенные выкладки можно уверенно заявить, что явление, именуемое как l/f-шум, по крайней мере, в ряде случаев, может быть результатом пуассоновского процесса. Подобранная экспериментаторами аппроксимирующая эмпирическая формула c/f искусственна. При сверхнизких частотах формула c/fy может достаточно точно описывать эти процессы, но в связи с искусственностью эмпирической формулы c/fy ее применение ограничено, откуда и появились пределы степени у.
Так как формула (2) не привязана к конкретной физической среде и конкретным физическим объектам, то соответственно шум, генерируемый по данной модели, будет проявляться в любых средах, с любыми объектами, где будут создаваться соответствующие условия. Этим и объясняется повсеместное проявление l/f-шума.
СПИСОК ЛИТЕРАТУРЫ:
- Холкин В.Ю. Модель Барьерного механизма возникновения l/f-шума в полупроводниковых устройствах.//Изв. вузов. Приборостроение.2008. Т.51,№1.
- Beutler F.J., Leneman O.A.Z. (1968) , The spectral analysis of impulse processes, Information and Control, 12, 236-258.
- Кешнер М.С. Шум типа 1/f // «Академия Тринитаризма», М., Эл № 77-6567, публ. 10993, 10.02.2004.
- Bell D.A. - J. Phys. Ser. С, 1980, v. 13, p. 4425.
- Hooge F. N. et al. Rept. Progr. Phys., 1981, v. 44, p. 479.
- Френке Л. Теория сигналов: Пер. с англ./ Под ред. Д.Е. Вакман - М.: Советское радио, 1974.
Библиографическая ссылка
ОБОСНОВАНИЕ ВОЗНИКНОВЕНИЯ l/f-ШУМА В ЭЛЕКТРОННЫХ СХЕМАХ ПРИБОРОВ // Фундаментальные исследования. 2009. № 4. С. 44-46;URL: https://fundamental-research.ru/ru/article/view?id=4360 (дата обращения: 25.12.2025).



