В процессе производства валовой продукции появляются производственные отходы, которые причиняют немалый вред окружающей среде. Некоторые хозяйствующие субъекты перерабатывают свои производственные отходы и применяют полученный продукт повторно, а другие хозяйствующие субъекты ликвидируют их. Как в первом, так и во втором случае появляются вторичные отходы. Существуют модели, учитывающие производственные отходы и учитывающие вторичные отходы, появляющиеся в процессе ликвидации первичных производственных отходов.
Так как на сегодняшний день состояние окружающей среды актуально, то немалое значение имеет переработка (ликвидация) производственных отходов с наименьшими затратами и наименьшими вторичными отходами, появляющимися в процессе их переработки.
Цели исследования: разработка методики неотрицательного решения балансовой модели, учитывающей производственные отходы; создание программы по алгоритму, разработанному из результатов разработанной методики; разработка модели межотраслевого баланса АО Агрокомбинат «Южный»; применение созданной программы для нахождения решения модели АО Агрокомбинат «Южный».
Материалы и методы исследования
В работе были применены численные методы и язык программирования. Использованы статистические данные АО Агрокомбинат «Южный».
Результаты исследования и их обсуждение
Рассмотрим модель Леонтьева – Форда [1, c. 96]:
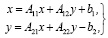 , (1)
, (1)
где x ∈ Rn – вектор валового продукта;
y ∈ Rm – вектор производственных отходов;
b1(n) – вектор чистого выпуска полезного продукта;
b2(m) – вектор остатка ликвидированных отходов;
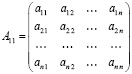 – матрица, которой характеризуются прямые затраты;
– матрица, которой характеризуются прямые затраты;
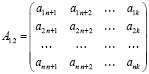 – матрица, которой характеризуются затраты ликвидации производственных отходов;
– матрица, которой характеризуются затраты ликвидации производственных отходов;
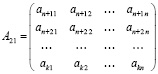 – матрица, которой характеризуется величина производственных отходов;
– матрица, которой характеризуется величина производственных отходов;
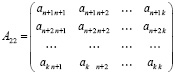 – матрица, которой характеризуются размеры новых вредных отходов, которые появляются в процессе ликвидации производственных отходов;
– матрица, которой характеризуются размеры новых вредных отходов, которые появляются в процессе ликвидации производственных отходов;
Представим (1) в виде
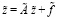 , (2)
, (2)
где 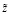 является блочным вектором:
является блочным вектором:
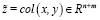 ;
;
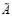 является блочной матрицей:
является блочной матрицей:
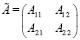 ; (3)
; (3)
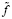 является блочным вектором:
является блочным вектором:
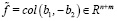 .
.
Из (2) следует, что
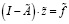 , (4)
, (4)
где I является единичной матрицей.
В (4) обозначим 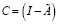 , то
, то
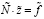 . (5)
. (5)
В процессе решения модели (1) появляются некоторые вопросы:
Первый вопрос касается существования неотрицательного решения (1). Если вопрос о существовании неотрицательного решения (1) принимает положительный результат, то возникает второй вопрос о его единственности. Если (1) обладает неотрицательным единственным решением, то следует выяснить, какие методы можно применить для её решения.
Поэтому требуется уточнить устойчивость решения (1) относительно погрешностей начальных данных. В случае, когда (1) будет обладать погрешностью из-за большой её размерности и небольшими погрешностями её начальных значений, то она может получить результат как с большими погрешностями, так и с небольшими погрешностями.
Известно, что устойчивость решения (1) зависит от числа обусловленности 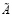 , то есть если
, то есть если 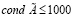 , то рассматриваемая модель будет обладать устойчивым решением, иначе – неустойчивым решением.
, то рассматриваемая модель будет обладать устойчивым решением, иначе – неустойчивым решением.
Для первого случая будем применять итерационный метод [2, с. 60], а во втором – метод регуляризации [3–5].
Известно, что модель (1) является продуктивной, если выполняются следующие условия:
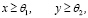 (6)
(6)
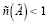 , (7)
, (7)
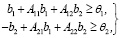 , (8)
, (8)
где 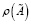 является спектральным радиусом блочной матрицы
является спектральным радиусом блочной матрицы 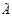 ;
;
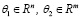 являются нулевыми векторами.
являются нулевыми векторами.
В том случае, если условия (6), (7), (8) принимают истинные значения, то к решению (1) сходится следующее последовательное приближение
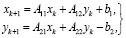 , (9)
, (9)
k = 0, 1, 2, …
при ∀(x0, y0) x0 ∈ Rn, y0 ∈ Rm .
Рассмотрим случай, когда 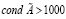 .
.
Так как мы применяем вместо точных значении величин модели их приближенные значения, то в (5) заменим C через 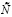 , а
, а 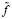 через
через 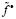 , тогда
, тогда
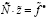 . (10)
. (10)
Пусть 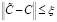 ,
, 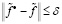 .
.
Из [4], [5] известно, чтобы отыскать решение (10) необходимо найти 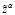 и вычислить
и вычислить
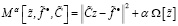 ,
,
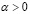 , (11)
, (11)
где 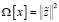 – стабилизирующий функционал,
– стабилизирующий функционал,
α = α(δ) – параметр регуляризации.
Существует единственный 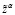 , который можно определить при всяком фиксированном α > 0 [4], [5]:
, который можно определить при всяком фиксированном α > 0 [4], [5]:
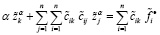 ,
,
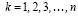 . (12)
. (12)
Опишем следующий алгоритм, составленный на основании изложенных методик:
1. Вводим n, m.
2. Вводим численные значения A11 – (n × n), A12 – (n × m), A21 – (m × n), A22 – (m × m).
3. Вводим численные значения b1 – (n), b2 – (m).
4. Строим (3).
5. Если cond A ≤ 1000, то переходим к шагу 6, иначе переходим к шагу 12.
6. Задаём значения (x0, y0).
7. Задаём значение ε > 0.
8. Проверяем выполнимость (6).
9. Проверяем выполнимость (7).
10. Проверяем выполнимость (8).
11. Если выполнены условия (6), (7), (8), то для вычислений применяем (9) до достижения требуемой погрешности ε > 0.
12. Строим 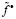 .
.
13. Задаём α1 > 0.
14. При α1 производим подсчёт 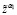 выражения (12).
выражения (12).
15. При α1, 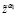 , подсчитываем
, подсчитываем 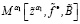 по формуле (11).
по формуле (11).
16. Задаём α2 > 0, α2 < α1.
17. При α2, производим подсчёт 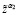 выражения (12).
выражения (12).
18. При α2, 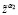 , подчитываем
, подчитываем 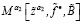 по формуле (11).
по формуле (11).
19. Если 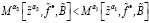 , то перейти к шагу 21.
, то перейти к шагу 21.
20. Если 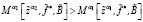 , то
, то 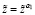 .
.
21. Задаём α3 > 0, α3 < α2.
22. При α3, производим подсчёт 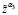 выражения (12).
выражения (12).
23. При α3, 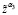 , подсчитываем
, подсчитываем 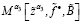 по формуле (11).
по формуле (11).
24. Если 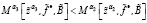 , то перейти к шагу 26.
, то перейти к шагу 26.
25. Если 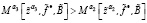 , то
, то 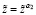 .
.
26. Задаём α4 > 0, α4 < α3.
Эти расчёты продолжаем до того, пока на (k + 1)-м шаге не будет найдено 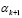 ,
, 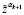 , при которых
, при которых
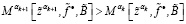 .
.
Тут полагаем, что 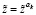 , и завершаем вычисления.
, и завершаем вычисления.
По данным разработанного алгоритма была создана программа на ЭВМ.
Из усреднённых статистических данных за 2019–2021 гг. построим принципиальную схему межотраслевого баланса АО Агрокомбинат «Южный» (таблица).
Из таблицы получим
 ,
,
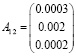 ,
,
A21 = (0.1 0.099 0.03), A22 = (0)
Принципиальная схема межотраслевого баланса АО Агрокомбинат «Южный» (тыс. руб.)
|
Производящие секции |
Потребляющие секции |
Затраты на ликвидацию производственных отходов |
Конечный спрос |
Валовый выпуск |
||
|
секция 1 |
секция 2 |
секция 3 |
||||
|
Секция «Огурец зимне-весенний» |
49493,8 |
0 |
0 |
3503,7 |
111804,65 |
1167890.7 |
|
Секция «Огурец осенний» |
0 |
57157,2 |
0 |
3903,6 |
137632,24 |
195179.8 |
|
Секция «Томаты» |
0 |
0 |
63234,6 |
204,64 |
1278042,4 |
1341481.6 |
|
Производственные отходы |
116789,1 |
19518 |
40244,4 |
|||
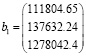 ,
,
b2 = (0)
Пусть к концу 2023 г. АО Агрокомбинат «Южный» запланирует, увеличит продукцию секции, идущую на конечное потребление, на 12 % по сравнению с данными, приведёнными в таблице, то есть:

Введя исходные и запланированные данные в созданную программу, получим следующий результат:
 ,
,
y = (2287246.1)
Таким образом, к концу 2023 г. АО Агрокомбинат «Южный», чтобы удовлетворить запланированный конечный спрос, должен будет произвести валовую продукцию:
− секции «Огурец зимне-весенний», равную 15140927,37 тыс. руб.,
− секции «Огурец осенний», равную 2526469,99 тыс. руб.,
− секции «Томаты» – 17434426,7 тыс. руб.,
− производственные отходы составят 2287246,1 тыс. руб.
Заключение
Таким образом, была разработана методика неотрицательного решения балансовой модели, учитывающей производственные отходы. По её результатам была создана программа, проверяющая, является ли решение модели устойчивой или нет к погрешностям исходных данных и к погрешностям, возникающим из-за её большой размерности и выбрать метод решения модели относительно полученного результата. С помощью созданной программы найдено неотрицательное решение разработанной балансовой модели АО Агрокомбинат «Южный». Результаты исследования были переданы АО Агрокомбинат «Южный».
Библиографическая ссылка
Асхакова Ф.Х., Лайпанова З.М., Мамчуев A.M., Урусова А.С. РЕШЕНИЕ БАЛАНСОВОЙ МОДЕЛИ АО АГРОКОМБИНАТ «ЮЖНЫЙ» // Фундаментальные исследования. 2022. № 5. С. 7-10;URL: https://fundamental-research.ru/ru/article/view?id=43245 (дата обращения: 02.01.2026).
DOI: https://doi.org/10.17513/fr.43245



