Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Нугаева Д.А. 1 Лизунова Е.Д. 1 Струкова А.А. 1

---

1 Российский экономический университет им. Г.В. Плеханова

Выбор оптимального по экономическому критерию варианта организации денежных и материальных потоков производственной сферы предприятия – актуальная с позиции повышения его эффективности и конкурентоспособности по затратам задача, решение которой включается в процесс разработки рыночной и внутрифирменной стратегий. До настоящего времени эта задача широко не освещена в экономической литературе: отсутствуют обоснованные постановки задач оптимизации, не в полной мере разработаны оптимизационные модели и не представлены практические расчеты оптимальных вариантов. В настоящей публикации авторы рассматривают эти задачи в приложении к предприятию, функция «затраты – выпуск» которого корректно описывается неоклассической производственной функцией. Приводятся соответствующие этому варианту постановка задачи, собственно динамическая модель, перечень критериев оптимальности и рисковых ограничений, результаты расчетов по динамической модели для различных комбинаций экзогенных и эндогенных параметров. В частности, показано, что степень однородности производственной функции оказывает определяющее влияние на динамику выпуска, увеличивая затраты в случае планирования высоких объемов производства. Среди управляемых параметров модели важную роль играет темп инвестиций в рабочий капитал предприятия из собственных источников, повышая/снижая выпуск. Ограничение на риск структуры рабочего капитала оказывает определяющее влияние на динамику результата в производственной сфере: с ростом норматива финансовой зависимости выпуск растет быстрее риска банкротства по причине высокой отдачи рычага капитала.

Статья в формате PDF

435 KB

производственная сфера предприятия

рабочий капитал

неоклассическая производственная функция

динамическая модель производственной сферы предприятия

критерии оптимальности

риск структуры рабочего капитала

управляемые и неуправляемые параметры

методы оптимизации

1. Maximov D.A., Khalikov M.A. Prospects of institutional approach to production corporation assets assessment. Actual Problems of Economics. 2016. V. 183 № 9. P. 16–25.

2. Бельченко С.В., Халиков М.А., Щепилов М.В. Управление трансакционными издержками интегрированной группы предприятий: Модели и методы. М.: ЗАО «Гриф и К °», 2011. 172 с.

3. Халиков М.А. Методы анализа и оценки риска рыночной деятельности подразделений иерархической производственной структуры // Менеджмент в России и за рубежом. 2009. № 1. С. 108–120.

4. Антиколь А.М., Халиков М.А. Нелинейные модели микроэкономики: учеб. пособие. М.: ФГБОУ ВПО «РЭУ им. Г.В. Плеханова», 2011. 156 с.

5. Бабаян Э.А., Расулов Р.М., Халиков М.А. Динамические модели «затраты-выпуск» // Экономика природопользования. 2013. № 2. С. 3–16.

6. Безухов Д.А., Халиков М.А. Выбор оптимального варианта обновления основного капитала предприятия с учетом рисков производственной сферы // Фундаментальные исследования. 2015. № 4. С. 191–198.

7. Клейнер Г.Б. Производственные функции: теория, методы, применение. М.: Финансы и статистика, 1986. 239 c.

8. Халиков М.А., Максимов Д.А. Об одном подходе к анализу и оценке ресурсного потенциала предприятия // Международный журнал прикладных и фундаментальных исследований. 2015. № 11–2. С. 296–300.

9. Халиков М.А., Максимов Д.А. Концепция и теоретические основы управления производственной сферой предприятия в условиях неопределенности и риска // Международный журнал прикладных и фундаментальных исследований. 2015. № 10–4. С. 711–719.

10. Халиков М.А., Никифорова М.А., Модели оценки критического объема производства многономенклатурного предприятия с учетом рыночного риска // Фундаментальные исследования. 2017. № 11. С. 248–252.

11. Аоки М. Введение в методы оптимизации. Основы и приложения нелинейного программирования. М.: Наука, 1977. 343 с.

12. Грибов А.Ф. Нелинейная модель оптимизации операционной деятельности предприятия // Фундаментальные исследования. 2016. № 2–1. С. 140–144.

13. Горский М.А. Теоретический подход и численный метод поиска квазиоптимального решения нелинейной дискретной задачи большой размерности // Экономический журнал Высшей школы экономики. 2019. Т. 23. № 3. С. 465–482.

14. Максимов Д.А., Халиков М.А. Методы оценки и стратегии обеспечения экономической безопасности предприятия. М.: ЗАО «Гриф и К °», 2012. 220 с.

15. Безухов Д.А., Халиков М.А. Математические модели и практические расчеты оптимальной структуры производственного капитала предприятия с неоклассической производственной функцией // Фундаментальные исследования 2014. № 11–1. С. 114–123.

Объектом исследования в данной статье является предприятие акционерной формы собственности. Корпоративная форма собственности предполагает, что компания самостоятельно несет ответственность за прибыль и убытки.

Рассматриваемое в данной статье предприятие имеет три традиционных «центра инвестиций и прибыли»: производственный, финансовый и инвестиционный. Каждый из перечисленных центров ответственности имеет собственные денежные потоки.

В рамках данной статьи предполагается рассмотреть именно операционный сегмент, в котором образуется новая экономическая добавленная стоимость, представляющая для собственников и инвесторов наибольший интерес.

Эта публикация служит прямым продолжением исследований проф. М.А. Халикова по проблематике динамической оптимизации производственной сферы предприятия с критериями эффективности и рентабельности затрат, финансируемых из собственных и заемных источников и с ограничениями, включающими и ограничение на риск структуры пассивов рабочего капитала (здесь следует, в первую очередь, процитировать работы указанного коллектива авторов [1–3] и обратить внимание на исследования [4–6]). Отметим, что предлагаемая в статье постановка задачи динамической оптимизации является оригинальной в плане выбранного объекта приложения – рассматривается вариант предприятия, зависимость в паре «затраты – выпуск» которого корректно описывается неоклассической производственной функцией (см. работу Г.Б. Клейнера [7]).

Методологическую основу исследования составили работы отечественных и зарубежных ученых по:

1) проблемам моделирования производственной сферы предприятия в условиях неопределенности и риска [8, 9, 10];

2) оптимизации социально-экономических систем на микроуровне [11, 12];

3) методам дискретной оптимизации в непрерывной и дискретной постановках [13];

4) методам оценки и учета в моделях производственной сферы предприятия внешних и внутренних рисков [14].

Цель исследования – разработка инструментария моделей и методов анализа и регулирования денежных потоков производственного сегмента (производственной сферы) корпорации.

Ниже подробно рассмотрим экономико-математическую формализацию производственной сферы предприятия.

1. Постановка задачи и математическая модель денежных потоков

Производственная сфера предприятия задается системой выражений (1–15). Используя формулы, опишем алгоритм расчета:

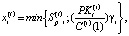(1)

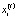– выпуск продукции i-й СБЕ на интервале t;

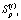– рыночный спрос на продукцию i-й СБЕ на интервале t;

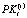– объем рабочего капитала i-й СБЕ в начале интервала t;

C(i) (1) – удельные затраты i-й CБЕ (затраты на единицу выпуска);

γi – степень однородности функции «затраты – выпуск» i-й СБЕ.

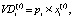(2)

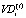– валовый доход i-ой СБЕ на интервале t;

pi – рыночная цена единицы продукции i-ой СБЕ;

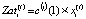(3)

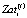– затраты производственной сферы i-ой СБЕ на интервале t;

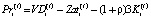(4)

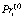– промежуточный продукт, сформированный в производственной сфере i-ой СБЕ на интервале t;

ρ – ставка по банковскому кредиту;

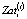– величина краткосрочного кредита, взятого на пополнение рабочего капитала i-ой СБЕ в начале интервала t;

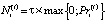(5)

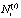– объем уплачиваемых налогов с промежуточного продукта i-ой СБЕ на интервале t;

τ – ставка налогообложения доходов подразделения холдинга;

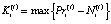(6)

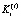– конечный продукт, сформированный в производственной сфере i-ой СБЕ на интервале t;

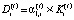(7)

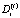– объем непроизводственного потребления i-ой СБЕ по завершении интервала t;

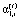– доля непроизводственного потребления в конечном продукте i-ой СБЕ на интервале t;

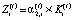(8)

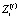– величина денежного потока средств, передаваемых в централизованный инвестиционный фонд холдинга по завершении интервала t;

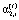– доля в конечном продукте перечислений в инвестиционный фонд холдинга для интервала t;

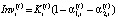(9)

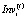– величина денежного потока собственных инвестиций в рабочий капитал производственной сферы i-ой СБЕ по завершении интервала t;

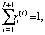
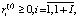(10)

I – число СБЕ в организационной структуре холдинга, I + 1 – индекс управляющей компании.

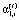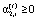; (11)

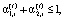
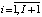
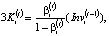
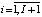(12)

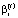– коэффициент риска структуры капитала i-ой СБЕ для интервала t.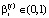

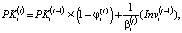(13)

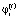– коэффициент амортизации рабочего капитала производственной сферы i-ой СБЕ на интервале t.

Изменения объема централизованного инвестиционного фонда холдинга:

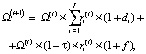(14)

f – ставка по депозиту на средства централизованного инвестиционного фонда, размещенные управляющей компанией на депозитах в коммерческих банках;

di – ставка по внутрифирменному кредиту;

Ω(t) – объем средств централизованного инвестиционного фонда холдинга на начало интервала t;

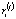– доля трансфертных отчислений в производственной сфере i-ой СБЕ из централизованного инвестиционного фонда холдинга в начале интервала t.

В описываемой модели часть параметров модели производственной сферы являются неуправляемыми (экзогенными). К ним относятся такие параметры, как: .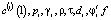

Приведем перечень эндогенных (управляемых) параметров модели производственной сферы подразделений холдинга интервала t:

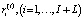устанавливает УК;

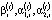устанавливает i-я СБЕ ().

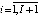Проведем модельные расчеты для следующего набора исходных данных: Ω = 500.

Данные по СБЕ и внешним показателям представлены в табл. 1 и 2.

Таблица 1

Показатели для рассматриваемой СБЕ

Таблица 2

Внешние показатели

Таким образом, все экзогенные и эндогенные параметры заданы, кроме коэффициента 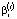риска структуры капитала.

Задача данной статьи – выбор вариантов управления эндогенными параметрами при определенных вариантах событий в рыночной среде.

Предполагается провести расчеты денежных потоков предприятия для последовательных значений коэффициента 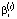= 0,2; 0,5; 0,7, сохраняя выбранное значение и на всех временных интервалах.

Для решения поставленной задачи для каждого значений 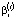= const и для каждого структурного подразделения i = 1,…,5 необходимо последовательно рассчитать конечный продукт 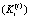, величину денежного потока средств, передаваемых в централизованный инвестиционный фонд холдинга 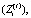и эффективность средств, вложенных в рабочий капитал, которая рассчитывается по формуле 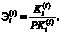(15):

(15)

Стоит отметить, что постановка задачи описывает регулирование внутрифирменной деятельности предприятий в составе холдинга. Задача непосредственно связана с этой тематикой, поэтому в дальнейшем будем индексом i отмечать рассматриваемую структурную бизнес-единицу в составе холдинга, подразумевая под ней одну структурную единицу.

2. Проведение расчетов на основе представленной модели для предприятия на интервале t от 1 до 10

Используя формулы и зависимости, приведенные ранее, мы рассчитали все необходимые величины и составили табл. 3, 4, 5 с графиками для СБЕ на интервале t при различных уровнях риска.

СБЕ при β1 = 0,2

Таблица 3

Расчеты показателей для уровня риска 0,2

Таблица 4

Расчеты показателей для уровня риска 0,5

Таблица 5

Расчеты показателей для уровня риска 0,7

Сравним рассчитанные коэффициенты при помощи графиков (рис. 1).

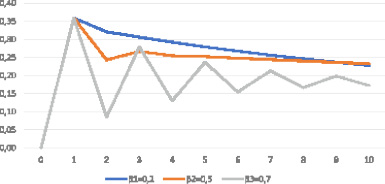
Рис. 1. Сравнение эффективности средств, вложенных в рабочий капитал

Вывод: из проведенных расчетов следует, что все показатели СБЕ снижаются с ростом коэффициента риска структуры.

3. При фиксированном коэффициенте риска определяем зависимость между масштабом производства и пороговым значением рабочего капитала, обеспечивающим положительную доходность производственной деятельности

В качестве фиксированного коэффициента риска выбираем β2 = 0,5. Далее рассмотрим показатели СБЕ при изменении значений начального уровня рабочего капитала. Результаты представлены в табл. 6.

Таблица 6

Сравнение доходности предприятия при различном уровне рабочего капитала за весь рассматриваемый период

Вывод: доходность СБЕ остается положительной даже при уменьшении рабочего капитала. Все показатели, характеризующие СБЕ, изменяются пропорционально исходному объему рабочего капитала.

4. Сравнительный анализа влияния коэффициента риска структуры рабочего капитала на финансовый результат

Рассмотрим доходность предприятия при различных коэффициентах риска. В качестве фиксированного коэффициента выберем β1 = 0,2 и рассмотрим табл. 7.

Таблица 7

Доходность предприятия при коэффициенте риска β1 = 0,2

При β1 = 0,2 доходность предприятия увеличивается с 158,7 удельной единицы до 5051,1 удельной единицы на протяжении всего интервала t.

Рассмотрим при β2 = 0,5 табл. 8.

Таблица 8

Доходность предприятия при коэффициенте риска β2 = 0,5

При β2 = 0,5 доходность предприятия увеличивается с 158,7 удельной единицы до 582,4 удельной единицы на протяжении всего интервала t.

Рассмотрим при β3 = 0,7 табл. 9.

Таблица 9

Доходность предприятия при коэффициенте риска β3 = 0,7

При β3 = 0,7 доходность предприятия увеличивается с 158,7 удельной единицы до 298,67 удельной единицы на протяжении всего интервала t.

На основе полученных результатов можно сделать вывод, что с ростом коэффициента риска уменьшается доходность предприятия. Это обусловлено тем, что последняя напрямую зависит от масштаба производства, который, в свою очередь, зависит от величины рабочего капитала, на которую влияет коэффициент риска. Связь этих параметров прослеживается в формулах (1), (2), (13).

5. Определение влияния уровня инвестиций этого раунда на конечный продукт следующего раунда

Рассмотрим влияние уровня инвестиций на конечный продукт при фиксированном значении β1 = 0,2 для рассматриваемой СБЕ.

Таблица 10

Зависимость величины конечного продукта от уровня инвестиций при фиксированном значении β1 = 0,2

Из табл. 10 видно, что при увеличении уровня инвестиций растет конечный продукт. Рассмотрим график зависимости на рис. 2.

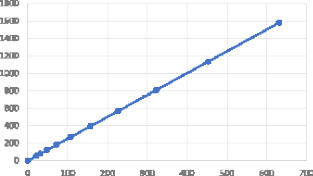
Рис. 2. Зависимость величины конечного продукта от уровня инвестиций при фиксированном значении β1 = 0,2

Из графика следует, что между уровнем инвестиций и конечным продуктом имеется линейная зависимость.

Выводы

Таким образом, была разработана модель для расчета методов анализа и регулирования денежных потоков производственного сегмента корпорации. Проведенный в этой статье анализ экономической динамики производственной сферы предприятия на основе формул (1)–(15) с неоклассической производственной функцией позволил сделать следующие выводы, часть из которых согласуется с выводами работ [4, 5, 15], полученными для производственной сферы компании.

1. Выбор эндогенных (управляемых) параметров производственной сферы предприятия в составе коэффициента финансовой зависимости предприятия от внешних источников финансирования и доли отчислений из прибыли на собственные инвестиции в рабочий капитал является обоснованным. Действительно, динамика производственной сферы в условиях локальных изменений этих параметров существенно отличается.

2. Основным экзогенным параметром модели является степень однородности производственной функции, характеризующая масштаб производства. Нелинейный характер зависимости от этого параметра определяется характером динамики: с ростом степени однородности наблюдается экспоненциальный рост, со снижением – экспоненциальное падение.

3. Актуальным продолжением начатых авторами в этой статье исследований являются поиск и обоснование так называемой точки перехода – такого значения показателя однородности, при котором предприятие не выигрывает и не проигрывает при незначительных изменениях риска структуры рабочего капитала и параметров распределения инвестиций из собственных и внешних источников финансирования в рабочий капитал.

Библиографическая ссылка