Работы Г. Марковица [1] и Дж. Тобина [2] являются основными в современной портфельной теории. Портфель Тобина – это комбинированный портфель, состоящий из рискованных и безрисковых активов и имеющий минимальный риск при заданной целевой доходности портфеля [2]. На практике в качестве безрискового актива часто рассматривают облигации федерального займа (ОФЗ) или государственные краткосрочные бескупонные облигации (ГКО), поскольку именно они имеют максимальный уровень надежности.
С появлением выбора безрискового актива как части инвестирования, лицо, принимающее решение, может приобрести этот актив, а также добавить его в уже рассматриваемый рискованный портфель. Соответственно, это расширяет множество инвестиционных возможностей, меняет вид и форму эффективной границы [1]. Инвесторы заинтересованы в выборе решения из «обновленного» эффективного множества, поэтому все изменения, возникшие при добавлении в рассматриваемый портфель безрискового актива, должны быть проанализированы.
Принятие решения инвестором на практике представляет собой постановку и решение следующих задач: оценка будущей доходности и измерение риска (для расчета которого используется дисперсия выборки [3, с. 451, 462]). Поскольку предполагается наличие на рынке безрискового актива, то получаем задачу о разделении предполагаемого инвестируемого бюджета в определённых долях между рыночной частью портфеля и безрисковым активом. Для этого следует провести анализ и численную оценку параметров возможных решений построенного комбинированного портфеля. В работе для этих целей используется метод количественных оценок, который в настоящее время является одним из основных инструментов для исследования области финансов и инвестиций.
Материалы и методы исследования
Пусть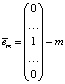 
-й единичный вектор; 
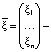вектор возможных доходностей рискованных активов (случайных величин); 
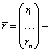вектор ожидаемых доходностей активов; 
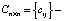ковариационная матрица доходностей активов; 
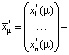вектор, описывающий структуру оптимального портфеля с целевой ожидаемой доходностью μ.
Утверждение. Имеет место линейная зависимость между ковариацией доходности оптимального портфеля с доходностью m-го актива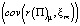 
и ожидаемой доходностью m-го актива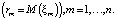 
Доказательство. По определению доходность оптимального портфеля будет равна
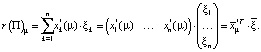
Ее ковариация с доходностью m-го актива ξm может быть записана следующим образом:
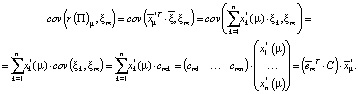
С учетом [4]
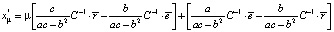
где
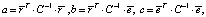
и того, что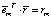 
, получаем
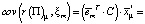
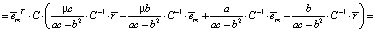
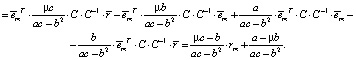
Таким образом, можем сделать вывод, что все точки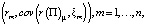 
лежат на одной прямой. То есть имеет место линейная связь.
Добавим теперь к множеству активов безрисковый актив F, имеющий доходность rf и риск ноль (то есть дисперсия доходности этого актива рана нулю). Сформируем новый портфель Π1 следующим образом:
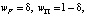
здесь Π – портфель, состоящий из первоначальных (рискованных) активов и имеющий структуру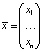 
(
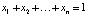). Тогда
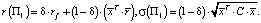
Геометрически инвестиционная возможность, соответствующая портфелю Π1, будет лежать на прямой, соединяющей точки (0, rf) и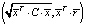 
(рис. 1).
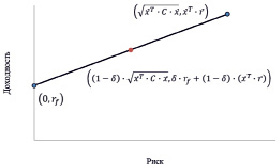
Рис. 1. Портфель Π1
Изменяя вес безрискового актива, очевидно, можно получить все точки отрезка. Таким образом, добавляя все такие прямые линии к множеству инвестиционных возможностей можно получить новое множество инвестиционных возможностей (с учетом наличия безрискового актива). Эффективная граница множества инвестиционных возможностей без учета безрискового актива – это, как известно, его подмножество, представляющее собой объединение всех недоминируемых возможностей. Технически (в результате всех вычислений) получается функция, выражающая зависимость риска портфеля от его ожидаемой доходности. Расширим теперь задачу поиска оптимального портфеля следующим образом: вектор структуры портфеля, вектор ожидаемых доходностей, вектор доходностей и ковариационная матрица дополняются безрисковой доходностью (весом актива с такой доходностью соответственно). Пусть вес безрискового актива составляет x0, доходность – rf. Тогда получаем
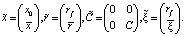
Поэтому расширенная задача оптимизации будет иметь следующий вид:
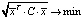
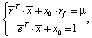
где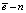 
-мерный вектор, состоящий из единиц.
Докажем следующую теорему:
Для расширенной модели Марковица (которая включает безрисковый актив) структура оптимального портфеля имеет следующий вид:
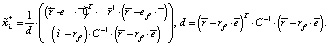
Все эффективные портфели в этом случае [5, c. 109] есть линейная комбинация безрискового актива (или портфеля со структурой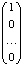 
и рыночного портфеля, имеющего структуру
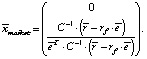(1)
Заметим, что рыночный портфель зависит от множества допустимых портфелей, состоящего из портфелей, формируемых из ценных бумаг, имеющихся на рынке.
Доказательство. Стандартный подход при решении задачи нелинейной оптимизации – метод множителей Лагранжа. Функция Лагранжа в этом случае будет иметь вид
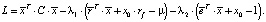
Далее следует составить систему уравнений, представляющих собой все частные производные этой функции, и приравнять их к нулю. В этом случае удобно записать функцию Лагранжа в явном виде
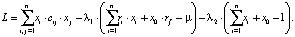
Для нахождения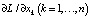 
можно, например, применить рассуждения, аналогичные проведенным авторами в работе [4]. Это приведет к уравнению
Остается еще найти частные производные по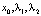 
. Имеем
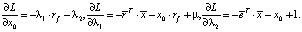
Следовательно, необходимо найти решение следующей системы уравнений:
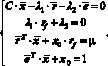
Из второго уравнения находим, что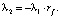 
В силу существования C-1 (из условия) первое уравнение системы дает вектор структуры портфеля 
:
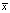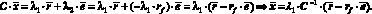
Подставим полученный результат в оставшиеся уравнения системы. Имеем
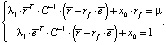
Применим правило Крамера для нахождения λ1. Определитель матрицы системы равен
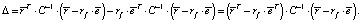
А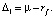 
Поэтому
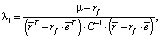
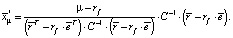
Из четвертого уравнения теперь легко находим, что
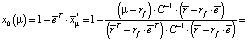
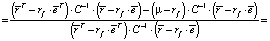
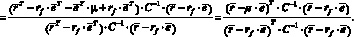
Теорема доказана.
Далее, заметим, что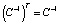 
(симметричность ковариационной, а значит, и обратной матрицы), а также что d – число. Следовательно, dT = d. Поэтому, если доходность рискованного портфеля с оптимальной структурой равна r(Π)μ, то риск (стандартное отклонение), соответственно, будет равен
=
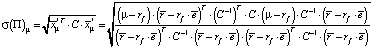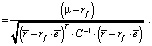
Доходность рыночного портфеля (по определению) есть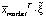 
. Тогда, с учетом (1), симметричности ковариационной, а значит, и обратной матрицы, а также того, что в знаменателе стоит число, его ожидаемая доходность и дисперсия будут равны
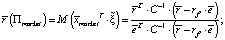(2)
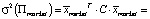
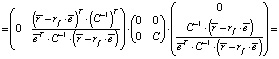
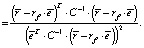(3)
Эффективная граница, как функция стандартного отклонения, будет в этом случае прямой линией, проходящей через точки (0, rf) и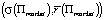 
(рис. 1) и имеющей (см. утверждение) следующее уравнение:
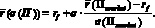(4)
Пусть Π – произвольный портфель со структурой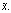 
Тогда, снова учетом (1) и свойств ковариационной матрицы, имеем
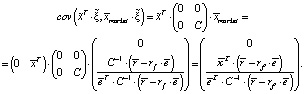(5)
Таким образом, мы снова получили, что ковариация представляет собой линейную функцию. На этот раз от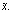 
Обозначив его доходность посредством r(Π) и используя тот факт, что его ожидаемая доходность складывается из ожидаемой доходности безрискового актива и рискованного портфеля, получаем
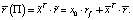
В силу того, что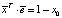 
последнее выражение можно переписать в виде
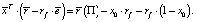(6)
Теперь легко установить линейную зависимость между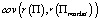 
и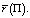 
Действительно, из (5) и (6) имеем
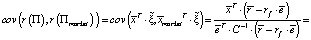
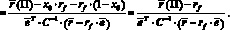(7)
Далее, из (2) и (3) можно сделать вывод, что
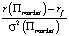
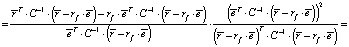
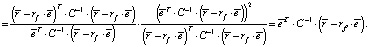
Теперь (7) можно переписать в виде
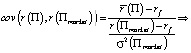
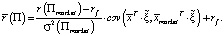
Поскольку (по определению [6, с. 509])
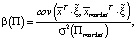
последнее уравнение можно переписать в виде
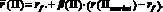
Величина в скобках здесь – это избыточная доходность рыночного портфеля. Теперь мы готовы доказать следующее
Утверждение. Для произвольного портфеля П верно следующее:
1) 
;
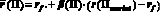2) 
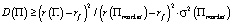. Строгое равенство будет иметь место тогда и только тогда, когда 
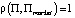(то есть портфель является эффективным);
3) 
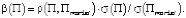Для эффективного портфеля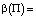 
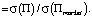
Доказательство. Нам осталось доказать только 2). Для произвольного портфеля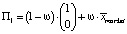 
, в котором вес рискованной части равен коэффициенту 
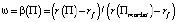ожидаемая доходность будет равна r(П). Действительно:
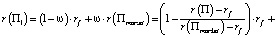
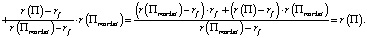
А сам портфель П1 будет лежать на эффективной границе. Следовательно, из (4) имеем
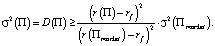
Из 1) следует, что
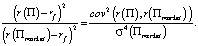
Применив к числителю дроби неравенство Коши – Буняковского [7, с. 105], получаем
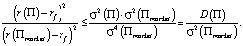
Равенство будет иметь место только в случае, если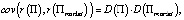 
то есть 
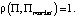Тем самым 2) доказано.
Результаты исследования и их обсуждение
Для лучшего понимания результатов рассмотрим продолжение примера, рассмотренного авторами в работе [4].
Пример [4]. Рассмотрим задачу добавления безрискового актива (ОФЗ SU52003RMFS9, купон 2,5 %) к следующему портфелю: акции ПАО «Центр международной торговли» (WTCMP), акции Волгоградэнергосбыт (VGSB), ПАО ТГК-1 (TGKA), акции Татнефть (TATNP) акции компании Селигдар (SELGP). Исходные данные загружены с сайта Московской Фондовой Биржи [8] (данные на 16.03.2021). Основные показатели рискованных активов представлены таблица, эффективная граница комбинированного портфеля на рис. 2.
Основные параметры активов портфеля
|
Параметры активов |
WTCMP |
VGSB |
TGKA |
TATNP |
SELGP |
|
Риск |
0,3537298 |
0,9027569 |
0,3520088 |
0,4142920 |
0,4825203 |
|
Ожидаемая доходность |
0,549179468 |
0,016211624 |
0,588725112 |
0,932287324 |
0,120334357 |
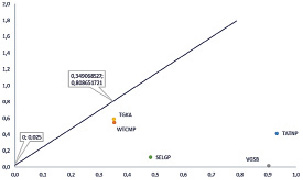
Рис. 2. Эффективная граница комбинированного портфеля: добавление в портфель ОФЗ SU52003RMFS9
То, что добавление безрискового актива принципиально изменило форму эффективной границы, показано на рис. 2. Очевидно, что введение в структуру портфеля безрискового актива существенно расширяет возможности инвестора, снижая его риски. Далее, рис. 3 демонстрирует вклад каждого из пяти рискованных активов в консолидированный риск портфеля. Такая картина позволяет инвестору понять, что увеличение доходности (а значит, и риска) комбинированного портфеля может быть достигнуто за счет короткой продажи самого низкодоходного актива (VGSB) и вложения всех свободных средств в самую перспективную компанию – «Татнефть» (что по факту приводит к скачкообразному увеличению ее доли в комбинированном портфеле). Переход за границу касательного портфеля приводит к тому, что добавление выбранной ОФЗ уже нецелесообразно: это очевидно из рис. 3 (доля безрискового актива в этой точке равна нулю). На рис. 2 и 3 – фактически наглядное руководство для инвестора по формированию комбинированного портфеля.
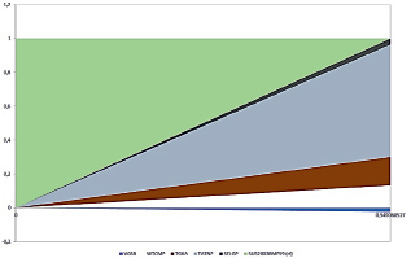
Рис. 3. Структура портфеля в случае включения в портфель ОФЗ SU52003RMFS9
Заключение
В работе рассмотрена теорема о том, что при существовании безрискового актива и портфелем рискованных активов, выбор инвестором – это выбор между безрисковым активом и тем же портфелем рисковых активов. Проведен анализ структуры комбинированного портфеля, влияющий на возможные решения инвестора. Для иллюстрации результата авторы исследовали и представили пример построения оптимального портфеля, содержащего безрисковый актив (на реальных данных российского фондового рынка). Построенный пример демонстрирует, что риск-аппетит инвестора определяется долей безрискового актива в комбинированном портфеле.
Библиографическая ссылка
Мочалина Е.П., Иванкова Г.В. ВЛИЯНИЕ СТРУКТУРЫ ПОРТФЕЛЯ НА РЕШЕНИЯ ИНВЕСТОРА: ДОБАВЛЕНИЕ БЕЗРИСКОВОГО АКТИВА // Фундаментальные исследования. – 2021. – № 11. – С. 146-154;URL: https://fundamental-research.ru/ru/article/view?id=43137 (дата обращения: 16.04.2024).