Рассмотрим задачу венчурного инвестора, распределяющего бюджет между несколькими инновационными проектами. Инвестор не может непосредственно оценить размер затрат на реализацию каждого из проектов из-за асимметрии знаний [1]. Вместе с тем инвестор знает, что изначально запрашиваемый инноватором бюджет избыточен и включает необязательные дополнительные затраты и резервы [1]. Одним из методов решения данной задачи является серия двусторонних переговоров с каждым из инноваторов. В ходе переговоров, при необходимости, производится дополнительная внешняя экспертиза проекта. Недостатком такого подхода является то, что при существенных дополнительных затратах его эффективность почти полностью зависит от качества внешней экспертизы, а, как показано в [1], для инновационных проектов асимметрия знания с высокой вероятностью существует и в системе «инноватор – эксперт». Другой подход состоит в использовании выявляющего механизма, когда инвестор предлагает инноваторам некоторое меню возможных решений, а инноваторы, выбирая конкретные решения, сигнализируют о своих внутренних оценках затрат на реализацию проекта.
Рассмотрим, например, ситуацию в модели инновационного инвестирования [1], когда инвестор с бюджетом B = 100 распределяет финансирование между двумя инновационными проектами. У каждого из проектов в модели есть две оценки стоимости выполнения – минимальные затраты Cmin и премиальные затраты Cextra. При этом оценка Cmin скрыта для всех, кроме самого инвестора, а оценка Cextra является публичной и выступает в качестве запрашиваемого бюджета. Предположим, что для проекта 1 Cmin = 30, Cextra = 50, а для проекта 2 Cmin = 60, а Cextra = 90. Таким образом, бюджет инвестора меньше общего запрашиваемого бюджета обоих проектов. Для того чтобы найти эффективное распределение бюджета, инвестор предлагает инноваторам некоторое финансирование в результате разделения общего бюджета (B1, B2), где B1 – финансирование первого проекта, а B2 – финансирование второго. Если оба инноватора согласны с данным предложением, проекты финансируются. Если один из инноваторов не согласен, бюджет перераспределяется в его пользу и поступает новое предложение от инвестора. Этот процесс происходит до тех пор, пока один из инноваторов не становится согласен на предлагаемый бюджет. Если в каком-то периоде оказывается, что оба не согласны, ни один из проектов не финансируется.
Предположим, что оба инноватора отвечают на предложение правдиво и инвестор начинает с предложения равного разделения бюджета (B1, B2) = (50, 50). Первый инноватор соглашается, поскольку предлагаемый бюджет больше его минимальных затрат, второй – не соглашается. Тогда инвестор предлагает новое разделение (B1, B2) = (45, 55), получает тот же ответ, затем (B1, B2) = (40, 60), на которое согласны оба инноватора. Первый проект получает, таким образом, финансирование размером 40, а второй – 60.
Непрямые выявляющие механизмы, использующие разделяющие меню типа «да/нет»? исследованы в современной литературе довольно хорошо [2–4]. В [2], в частности исследовано различие между издержками, связанными с определением правил распределения, и издержками, связанными с внедрением этих правил, и показано существование в подобных механизмах дополнительных издержек при определении платежей, совместимых по стимулам. В приведенном выше примере инвестор успешно распределяет бюджет при правдивом поведении инноваторов, но само правило не вызывает совместимости инноваторов по стимулам. Второй инноватор, очевидно, имеет стимулы не согласиться с финансированием в 60, поскольку оно не включает никакой премиальной части. Инвестор, однако, не получает из решений инноваторов никакой информации для того, чтобы даже ex post сформировать совместимое по стимулам распределение бюджета.
Целью исследования является построение механизма распределения для решения задачи венчурного инвестора, финансирующего несколько инновационных проектов. Мы предлагаем в качестве решения класс итеративных выявляющих механизмов динамического распределения ресурсов, состоящих из так называемых пороговых разделяющих вопросов и простого правила трансфера денежных средств типа pay as bid. В каждом раунде такого механизма инвестор предлагает распределение бюджета инноваторам. Инноваторы могут согласиться или отказаться, но не выдвинуть свое предложение (т.е. возможный ответ бинарен – либо «да», либо «нет»), и ответ «да» обязывает инноватора принять бюджет в данном размере. Инвестор в результате итеративного проведения такого опроса определяет цены инноваторов и формирует итоговое распределение бюджета.
При полной информации в таком механизме независимо от принципа определения предлагаемых распределений бюджета всегда существует эффективное распределение, представляющее собой равновесие Нэша, совершенное по подыграм.
Количество работ, посвященных дизайну механизмов в условиях высокой коммуникативной сложности, в последние два десятилетия растет очень быстро. Статичные однотоварные аукционные механизмы с ограниченным набором сообщений рассмотрены в [5; 6]. В [7] рассмотрены проблемы теоретической осуществимости оптимального правила распределения с учетов информационных характеристик в нескольких вариантах механизмов, в [3] предлагаются необходимые и достаточные условия для байесовской совместимости по стимулам, в [8] рассмотрен дизайн итеративного выявляющего механизма для однотоварного аукциона с ограниченной коммуникацией.
В данной работе рассмотрена мультиагентная система, в которой агенты (инноваторы) имеют квазилинейные функции полезности и принадлежат к одному из непересекающихся типов. Каждый инноватор имеет дихотомические предпочтения, т.е. результаты работы механизма попадают в один из двух классов – «хорошие» или «плохие». Более того, каждый инноватор одинаково оценивает каждый результат конкретного класса. Действительно, в примере, рассмотренном ранее, для определения ответа первого инноватора нет разницы, предлагает инвестор распределение (40, 60) или (50, 50) – в обоих случаях ответ инноватора будет положительным. Таким образом, тип агента можно представить одним значением – оценкой «хорошего» результата, приняв оценку «плохого» за ноль. Подобный подход к нормализации оценок широко применяется в литературе [4; 9]. Он позволяет с небольшими допущениями рассматривать механизмы организации распределения финансирования как из одного источника, так и из нескольких конкурирующих источников одновременно [10, 11]. При одновременном существовании нескольких конкурирующих предложений выявление предпочтений субъектов рынка затруднено, так как и для инноваторов, и для инвесторов в этом случае функция полезности усложняется. В таких случаях эффективными являются VCG-механизмы, которые ex post совместимы по предпочтениям [12, 13]. Заметим, что при этом количество взаимодействий (обменов сообщениями), необходимое для достижения оптимального распределения, экспоненциально растет с увеличением количества предложений [13].
Модель
Пусть N – множество всех инноваторов, получающих венчурное финансирование. Венчурный инвестор выбирает некоторое распределение бюджета x из конечного множества таких распределений X. Каждый инноватор характеризуется квазилинейной функцией полезности 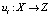 и имеет дихотомические предпочтения. Таким образом, функция оценки инноватора принимает вид:
и имеет дихотомические предпочтения. Таким образом, функция оценки инноватора принимает вид:
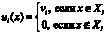
Примем, что vi принадлежит некоторому ограниченному сверху и снизу множеству возможных оценок V, которое известно всем участникам системы. Для каждого конкретного инноватора v совпадает с его минимальными затратами Cmin. Целью инвестора в такой системе является нахождение эффективного распределения бюджета:
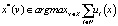 ,
,
где v = (vi, …, vi) – вектор оценок инноваторов.
Для упрощения предположим, что областью значений функций полезности является множество действительных чисел и что для любого состояния системы существует единственное оптимальное решение задачи распределения.
Функция совокупной общественной полезности W(u) в состоянии системы v определяется максимальной полезностью участников системы при оптимальной аллокации:
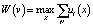 .
.
Таким же образом можно определить функцию совокупной общественной полезности для системы без конкретного участника i:
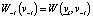 .
.
Результаты исследования и их обсуждение
В системе инновационного инвестирования, при взаимодействии инвесторов и инноваторов, естественно, стороны не могут наблюдать истинные значения оценок друг друга – ни инноваторы не знают размера бюджета инвестора, ни инвестор не может разделить минимальные затраты Cmin и премиальные затраты Cextra для каждого проекта. Для достижения рационального распределения инвестиционного бюджета инвестор в такой системе постепенно собирает информацию об инноваторах путем последовательных бинарных вопросов. Данная процедура построена следующим образом: инвестор одновременно предлагает некоторый бюджет всем инноваторам. При этом инвестор может даже раскрыть размер общего распределяемого бюджета. Когда инвестор предлагает бюджет pi, а инноватор i его принимает, это значит, что vi ≤ pi, т.е. минимально необходимый инноватору бюджет не больше, чем предложение инвестора. Шаг за шагом, предлагая различные распределения бюджета, инвестор определяет, в каких границах лежит vi для всех инноваторов. Например, то, что первый инноватор отказывается от распределения (40, …), но принимает распределение (70, …), значит, что его минимальные затраты Cmin лежат в границах [40, 70].
Определим итеративный распределяющий механизм (IAM) как многопериодную некооперативную игру следующим образом:
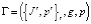 .
.
Здесь t – раунд игры, Jt – множество инноваторов, которым инвестор предлагает распределение бюджета, g – функция выбора инноватора (да/нет, в зависимости от оценки инноватора ui(x)), p – правило определения предлагаемой доли бюджета (правило перераспределения инвестором общего бюджета). Пусть 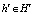 – история игры в конце раунда t. Бюджет, который предлагается инноватору i, определяется как
– история игры в конце раунда t. Бюджет, который предлагается инноватору i, определяется как 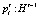 . Без потери общности можно предположить, что для каждого раунда t, каждой истории
. Без потери общности можно предположить, что для каждого раунда t, каждой истории 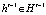 и каждого рационального инноватора
и каждого рационального инноватора 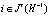 ,
, 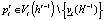 , где
, где 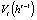 – множество возможных оценок инноваторов при данной истории игры. Каждый инноватор в момент времени t принимает решение об участии в распределении бюджета {«да», «нет»}. Игра останавливается в момент времени T, когда
– множество возможных оценок инноваторов при данной истории игры. Каждый инноватор в момент времени t принимает решение об участии в распределении бюджета {«да», «нет»}. Игра останавливается в момент времени T, когда 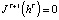 . Пример общего дерева игры для простого случая при двух инноваторах и достаточном для финансирования всех проектов бюджете (распределяемый бюджет больше, чем сумма Cmin всех инноваторов) представлен на рис. 1. Если распределяемый бюджет окажется меньше, чем сумма Cmin всех инноваторов (например, если в нашем примере
. Пример общего дерева игры для простого случая при двух инноваторах и достаточном для финансирования всех проектов бюджете (распределяемый бюджет больше, чем сумма Cmin всех инноваторов) представлен на рис. 1. Если распределяемый бюджет окажется меньше, чем сумма Cmin всех инноваторов (например, если в нашем примере 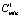 = 70,
= 70, 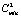 = 50), то из списка потенциальных получателей финансирования исключается случайным образом один из инноваторов, и игра проводится заново. Таким образом, для инноватора процесс
= 50), то из списка потенциальных получателей финансирования исключается случайным образом один из инноваторов, и игра проводится заново. Таким образом, для инноватора процесс 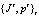 описывает дерево игры, в котором каждый узел порождает два последующих узла (рис. 2), а g и p – это функции, отображающие каждый конечный узел (лист) этого дерева в некоторое распределение бюджета.
описывает дерево игры, в котором каждый узел порождает два последующих узла (рис. 2), а g и p – это функции, отображающие каждый конечный узел (лист) этого дерева в некоторое распределение бюджета.
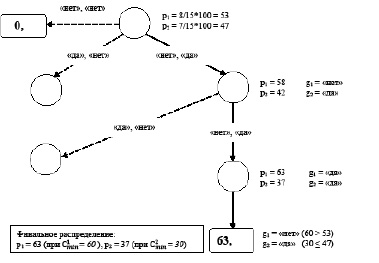
Рис. 1. Фрагмент общего дерева игры с двумя инноваторами (распределяемый бюджет = 100,
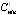 = 60,
= 60, 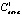 = 80,
= 80, 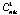 = 30,
= 30,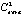 = 70, начальный шаг = 5)
= 70, начальный шаг = 5)
Всем участникам механизма – как инвестору, так и инноваторам – известна вся информация о прошлых раундах. Равновесие в таком механизме является совершенным по подыграм равновесием Нэша. Если коммуникация между участниками механизма проходит в режиме cheap talk, т.е. без транзакционных издержек, и нет ограничений по количеству раундов игры или ее продолжительности, то инвестор предлагает много последовательных распределений бюджета, пока эффективное распределение не будет найдено. Итеративный распределяющий механизм приводит к эффективному распределению при некоторой истории h, если существует распределение 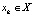 и
и 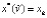 для всех
для всех 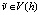 . Назовем эффективным такой распределяющий механизм, который всегда приводит к эффективному распределению, если все участники действуют в соответствии со своими истинными предпочтениями.
. Назовем эффективным такой распределяющий механизм, который всегда приводит к эффективному распределению, если все участники действуют в соответствии со своими истинными предпочтениями.
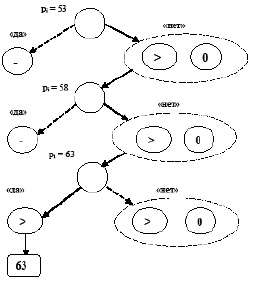
Рис. 2. Фрагмент дерева игры для инноватора i (указаны выигрыши игрока i)
В эффективном итеративном распределяющем механизме для инновационного инвестирования инвестор должен предлагать новое распределение бюджета каждый раунд, пока эффективное распределение не будет достигнуто. Вместе с тем предлагаемый механизм совершенно необязательно нуждается в выявлении точных минимальных затрат Cmin каждого инноватора. Другим преимуществом предлагаемого механизма является возможность использования различных процессов организации раундов – это могут быть аукционные механизмы с растущей ценой, с уменьшающейся ценой, с увеличением количества инноваторов и т.д.
Легко убедиться, что во множестве экономических систем с дихотомичными предпочтениями агентов и затратными сигналами [14] общая функция полезности для коалиции агентов может не быть субмодулярной. Субмодулярность предполагает выполнение условия субституциарности, а дихотомичные предпочтения, чаще всего, напротив, проявляют свойства комплементарности. Например, это характерно для задачи финансирования общественного блага, где при условии затратных сигналов невозможно создание механизма в форме английского аукциона с VCG-результатом.
Предположение о cheap talk значительно облегчает создание нашего механизма, но все же существуют системы, для которых достижение эффективного ex post равновесия невозможно [2]. Это происходит, так как эффективное ex post равновесие предполагает VCG-эквивалентный механизм, а итеративный распределяющий механизм может не собрать достаточно информации для расчета VCG-результатов [15]. Вместе с тем известно, что каждое эффективное распределяющее правило реализуется как равновесие Байеса–Нэша [2].
Вместе с тем для многих систем, в частности для системы инновационного инвестирования, итеративный распределяющий механизм можно создать и он допускает различные формы реализации в зависимости от конкретной системы.
Заключение
Для ряда экономических систем, в частности для системы финансирования инновационных проектов, итеративный распределяющий механизм является эффективным механизмом аллокации бюджетов в условиях неопределенности и скрытых предпочтений агентов. Итеративный распределяющий механизм, описанный в статье, принадлежит к классу динамических непрямых выявляющих механизмов. В данном механизме распределяющий ограниченный бюджет инвестор итеративно предлагает варианты распределения и определяет эффективное распределение после серии таких предложений. При полной информации и дихотомичных выявленных предпочтениях эффективное распределение является совершенным по подыграм равновесием Нэша независимо от способа предложения вариантов распределения. В условиях неопределенности способ предложения вариантов распределения имеет значение – оптимальное решение находится при его организации в одной из форм английского аукциона. Вместе с тем итеративный распределяющий механизм не обязательно существует для каждой конкретной системы с независимыми агентами, не согласованными по предпочтениям.
Работа выполнена при поддержке Российского фонда фундаментальных исследований, по гранту № 19-010-00376 А.
Библиографическая ссылка
Гуртуев А.О., Деркач Е.Г., Сабанчиев А.Х., Иванов З.З. РАСПРЕДЕЛЯЮЩИЙ МЕХАНИЗМ С МНОГОПЕРИОДНЫМ ВЫЯВЛЕНИЕМ ПРЕДПОЧТЕНИЙ ДЛЯ СИСТЕМЫ ИННОВАЦИОННОГО ИНВЕСТИРОВАНИЯ С УЧЕТОМ НЕОПРЕДЕЛЕННОСТИ // Фундаментальные исследования. 2021. № 10. С. 37-42;URL: https://fundamental-research.ru/ru/article/view?id=43106 (дата обращения: 31.01.2026).
DOI: https://doi.org/10.17513/fr.43106



