Использование математических методов способствовало зарождению экономической науки. Применение математики к экономике обеспечило исследование и объяснение изменения спроса и предложения, рыночного равновесия, построения производственной функции и т.д. Математика на макроуровне обеспечивает решение задач выбора монетарной политики, формирования антициклической политики, прогнозирования экономического роста, занятости, объемов внешней торговли и изменения мировых рынков. На микроуровне математика решает задачи оценки и предсказания изменения спроса, предложения, поведения потребителей, оказывающихся под влиянием различных факторов, но наибольшую ценность математика несет в ее применении в организации производства. Вопрос выбора направления хозяйственной деятельности является наиболее важным для предприятия, поскольку оно всегда стремится максимизировать прибыль, а следовательно, снизить затраты и увеличить выручку. Данной цели можно достичь, применяя математические инструменты в поиске оптимальной производственной политики, обеспечивающей максимальную прибыль [1, с. 936].
Целью исследования является изучение практики применения экономико-математических методов в решении задачи оптимизации производственных процессов, снижения затрат и максимизации прибыли.
Объектом исследования выступают производственно-экономические отношения, возникающие в процессе планирования хозяйственной деятельности, оптимизации производственных процессов, сокращения затрат и максимизации прибыли хозяйствующих субъектов.
Материалы и методы исследования
В исследовании производилась оптимизация производства двух видов напитков с использованием графического метода линейного программирования, также рассматривался случай его применения для целочисленного линейного программирования. Наглядная интерпретация исходных и полученных в ходе работы данных была произведена в табличной и графической форме.
Материалы исследования были сформированы на основе работ отечественных и зарубежных ученых, опубликованных в ведущих рецензируемых изданиях из перечней ВАК и включаемых в международные базы данных, а также на основе учебно-методических работ.
Результаты исследования и их обсуждение
Рассмотрим простой, но реальный экономический процесс. Например, имеется фирма, которая выпускает 2 вида напитков: пиво и квас. Для изготовления пива используются 4 исходных продукта: вода, солодовый концентрат, сахар, дрожжи. Для изготовления кваса используются 4 исходных продукта: вода, хлебный концентрат, сахар, дрожжи. Сырье следует подбирать таким образом, чтобы оно использовалось и для одного, и для другого продуктов, в данном случае общими ресурсами являются вода, сахар и дрожжи. Также возможны случаи использования определенного сырья только для одного из конечных продуктов производства: так, для пива требуется солодовый, а для кваса – хлебный концентрат.
Следующий момент, на который нужно обратить внимание, – это количественные данные, т.е. расходы исходных продуктов на 1 л продукции и суточные запасы (табл. 1).
Таблица 1
Исходные данные модели (начальное условие)
|
Исходный продукт |
Расход на 1 л |
Запасы |
|
|
Пиво |
Квас |
||
|
Вода |
1,2 |
1,1 |
462 л |
|
Солодовый концентрат |
90 |
− |
22 500 г |
|
Хлебный концентрат |
− |
30 |
12 000 г |
|
Сахар |
20 |
50 |
20 000 г |
|
Дрожи |
10 |
7 |
3 500 г |
Кроме требований к запасам сырья, могут предъявляться и иные. Например, в связи с проведением чемпионата мира по футболу суточный спрос на пиво превышает спрос на квас, однако не более чем в 3 раза. Кроме того, установлено, что спрос на пиво не превышает 80 л за сутки. Для упаковки продукции фирма использует пластиковые бутылки объемом 1 л и в день может использовать не более 400 бутылок.
Обычно бывают два основных вопроса: составить оптимальный план производства продукции либо с наибольшей прибылью, либо с наименьшими затратами. Выбираем наибольшую прибыль, однако не хватает данных о цене продукции, значит, их следует добавить [2, с. 45].
Розничная цена за 1 л пива составляет 100 рублей, за 1 л кваса – 50 рублей. Целью экономико-математической задачи является найти количество пива и кваса, которое должна производить фирма, чтобы прибыль от реализации была наибольшей.
При введении переменных нужно отталкиваться от вопроса задачи, поэтому за x1 и x2 примем соответственно количество пива и кваса, выпускаемое фирмой в сутки, выраженное в литрах, значит, по смыслу задачи x1 ≥ 0, x2 ≥ 0. Для изготовления напитков требуется определенное соотношение ресурсов, а также нужно учесть, что потребление ресурсов не может превышать их запасов, значит, определены первые условия системы ограничений: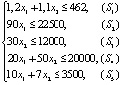 
.
Здесь используются ресурсы: S1 – вода, S2 – солодовый концентрат, S3 – хлебный концентрат, S4 – сахар, S5 – дрожжи.
Далее нужно перевести оставшиеся дополнительные условия о суточной разнице спроса на напитки, об ограничениях в количестве 400 бутылок и в количестве пива 80 л, т.е. дописать условия x1 – 3x2 ≤ 0, x1 + x2 ≤ 400 и x1 ≤ 80. Эти неравенства соответствуют ресурсам: S6 – разница суточных спросов пива и кваса, S7 – количество используемых бутылок, S8 – спрос на пиво в сутки.
Целевая функция – это прибыль от реализации продаж, значит, F = 100x1 + 50x2 → max.
Задачи линейного программирования характеризуются некоторыми общими чертами. В каждой из них элементы решения представляют собой ряд неотрицательных переменных. Требуется также выбрать значения этих переменных, чтобы: выполнялись некоторые ограничения, имеющие вид линейных неравенств или неравенств относительно переменных; некоторая линейная функция F тех же переменных обращалась в максимум (минимум) [3, с. 11]. Полученная математическая модель производства относится к классу задач линейного программирования: найти F = 100x1 + 50x2 → max при системе ограничений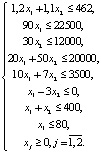 
.
Используя алгоритм графического метода, необходимо:
1) построить область допустимых реше- ний;
2) отметить вектор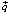 
, который проходит через точки (0;0) и (c1; c2), где c1 и c2 – коэффициенты при переменных в целевой функции. При определении максимума целевой функции направление вектора будет от точки (0;0) к точке (c1; c2), а при определении минимума – от точки (c1; c2) к точке (0;0);
3) изобразить линию уровня, проходящую через начало координат, т.е. прямую c1∙x1 + c2∙x2 = 0;
4) линию уровня переместить в направлении вектора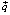 
. Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допустимых решений. Эта точка определяет единственное решение задачи линейного программирования и будет точкой экстремума.
Границы области допустимых решений находятся из системы ограничений путем замены знаков неравенств равенствами, т.е.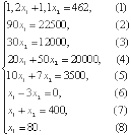 
Вектор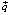 
будет направлен от начала координат к точке (100; 50), однако в целях удобства масштаба рисунка можно удвоить координаты, получив в итоге 
.
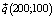Линия уровня F = 0 или 100x1 + + 50x2 = 0 перемещается в направлении вектора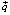 
до тех пор, пока линия уровня и область допустимых решений не будут иметь одну общую точку (на рис. 1(а) эта точка В). При этом значение целевой функции в этой точке равно Fmax = F(80, 320) = 24000.
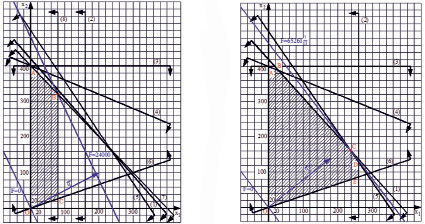
а) б)
Рис. 1. Нахождение оптимального решения графическим методом для начального условия (а) и измененного условия (б)
Подводя итог, можно отметить, что графическим способом был найден оптимальный план производства, а именно: если фирма будет производить за сутки 80 литровых бутылок пива и 320 литровых бутылок кваса, то можно получить наибольшую прибыль от продаж в размере 24 тыс. руб.
При решении многих экономических задач приходится рассматривать величины, принимающие только целые значения в силу своего экономического содержания. Подобные задачи относятся к задачам целочисленного линейного программирования [4].
Поскольку в результате решения задачи уже получилось решение x1 = 80, x2 = 320, то для целочисленного линейного программирования изменим условия. Запасы солодового концентрата равны 23 400 г, отсутствуют условия о том, что спрос на пиво не превышает 80 л за сутки и в день может использоваться не более 400 бутылок. Розничная цена за 1 л пива составит 180 рублей, за 1 л кваса – 140 рублей. Изменение условий задачи повлияет на составление математической модели. Теперь необходимо найти F = 180x1 + 140x2 → max при системе ограничений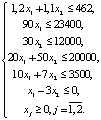 
Границы области допустимых решений также изменяются в соответствии с новой системой, т.е.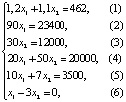 
, а вектор 
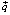будет направлен от начала координат к точке (180;140).
По рис. 1(б) точка оптимума – это точка С пересечения прямых (1) и (5); поскольку по графику видно, что она имеет нецелочисленные значения по осям координат, то найти координаты точки С можно, решив систему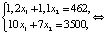 
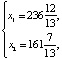а целевая функция примет значение 
.
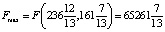Как видно из решения, фирме необходимо выпустить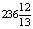 
литровых бутылок пива и 
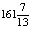бутылок кваса. Сделать это, конечно, не получится, поэтому требуется целочисленный ответ. Не всегда округление до целого значения в меньшую сторону обоих чисел дает наибольшую возможную прибыль, это зависит от соотношений сырья и его запасов, прибыли от продаж обоих напитков и иного, поэтому для нахождения целочисленного оптимума нужно увеличить часть рисунка возле точки С так, чтобы видна была каждая точка с целыми координатами в этой области. Линию уровня 
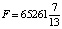двигаем в направлении, обратном направлению вектора 
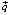, до тех пор, пока не найдем первую целочисленную точку. Если есть сомнения в нескольких точках, можно их координаты подставить в целевую функцию и выбрать среди полученных значений наибольшее (рис. 2) [5].
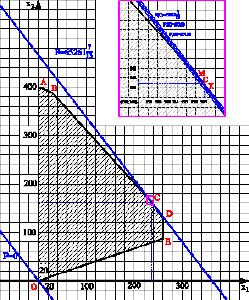
Рис. 2. Нахождение оптимального решения графическим методом для целочисленного программирования
Определим значения целевой функции для точек X(237;161) и M(236;162), эти точки принадлежат области допустимых решений системы ограничений и являются ближайшими к точке оптимума С: F(X) = 180∙237 + 140∙161 = 65200; F(M) = 180∙236+140∙162 = 65160. Тогда Fmax цел = F(237, 161) = 65200.
Перейдем к анализу полученных решений. На рис. 1(а) и 1(б) можно увидеть, что не все прямые являются контурами границы области допустимых решений. Так, на рис. 1(а) область ограничена только прямыми (6), (7) и (8), а также осями координат, следовательно, условия системы ограничений, соответствующие прямым (1), (2), (3), (4) и (5), являются избыточными. На рис. 1(б) лишним является условие о ресурсе «хлебный концентрат», т.е. условие, соответствующее прямой (3). Все это говорит о том, что имелись неточности в определении ограничений.
На этом этапе нужно еще раз вернуться к началу и убрать лишние неравенства или скорректировать ограничения. Задача считается качественной, если каждое условие образует одну из сторон многоугольника решений. Если, например, сдвинуть некоторые прямые или изменить их наклон, то они уже будут давать новые стороны области решений. Таким образом, можно уменьшить либо количество неравенств в системе, либо запасы, пропорции и т.д.
Создадим итоговое условие задачи. Имеется фирма, которая выпускает 2 вида напитков: пиво и квас. Для изготовления пива используются 4 исходных продукта: вода, солодовый концентрат, сахар, дрожжи. Для изготовления кваса используются 4 исходных продукта: вода, хлебный концентрат, сахар, дрожжи. Расходы исходных продуктов на 1 л продукции и суточные запасы приведены в табл. 2.
Таблица 2
Исходные данные задачи (итоговое условие)
|
Исходный продукт |
Расход на 1 л |
Запасы |
|
|
Пиво |
Квас |
||
|
Вода |
1,3 |
1,1 |
470 л |
|
Солодовый концентрат |
90 |
− |
23 400 г |
|
Хлебный концентрат |
− |
30 |
10 500 г |
|
Сахар |
20 |
50 |
18 000 гр |
|
Дрожи |
10 |
7 |
3 370 г |
В связи с проведением чемпионата мира по футболу суточный спрос на пиво превышает спрос на квас, однако не более чем в 3 раза. Для упаковки продукции фирма использует пластиковые бутылки объемом 1 л и в день может использовать не более 400 бутылок. Розничная цена за 1 л пива составляет 100 рублей, за 1 л кваса – 50 рублей.
Необходимо найти количество пива и кваса, которое должна производить фирма, чтобы прибыль от реализации продаж была наибольшей.
Математическая модель данной задачи имеет вид:
найти F = 100x1 + 50x2 → max при системе ограничений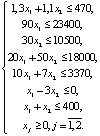 
Отметим границы области допустимых решений: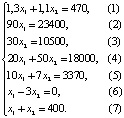 
Удваиваем коэффициенты перед неизвестными целевой функции, получив вектор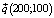 
. Точка оптимума G(260;110) (рис. 3) дает значение целевой функции Fmax = F(260, 110) = 31500.
Решение экономических задач с использованием методов математического моделирования позволяет осуществлять эффективное и рациональное управление производственным процессом на уровне прогнозирования и планирования экономических ситуаций [6, c. 9].
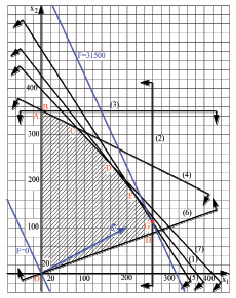
Рис. 3. Нахождение оптимального решения графическим методом для итогового условия
Приведенное исследование показало, что для получения наибольшей прибыли в размере 31,5 тыс. рублей фирме нужно производить за сутки 260 литровых бутылок пива и 110 литровых бутылок кваса.
В дальнейшем можно продолжить этот проект с помощью использования симплексного метода и двойственной задачи, сравнивать полученные разными методами результаты, например отметить, что допустимые симплексные решения X1, X2, X3 содержат координаты (x1; x2) точек О, H и G (рис. 3):
,
,
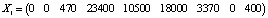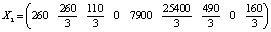Xопт =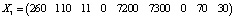 
.
Современная математика является для экономики, управления и финансов не только инструментом количественного расчета, но и методом исследования, а также средством формулировки задач исследования [7, с. 190].
Выводы
Таким образом, использование математических методов позволит добиться высоких результатов в решении экономических задач производства продукции. Навыками экономиста, необходимыми для решения экономических задач, являются умения переводить поставленные условия в математические операции, отрабатывать алгоритмы математических методов и способов решения. Заключительным этапом решения экономических задач являются корректировка и анализ полученных данных, что также требует математических знаний и соответствующих навыков. Математическая подготовка позволяет экономисту не только выполнять действия по определенному алгоритму, но и изменять условия и анализировать полученные результаты.
Библиографическая ссылка
Бредихина О.А., Головин А.А., Спицына А.О. ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И ИНСТРУМЕНТЫ В РЕШЕНИИ ЗАДАЧИ ОПТИМИЗАЦИИ // Фундаментальные исследования. – 2021. – № 9. – С. 5-11;URL: https://fundamental-research.ru/ru/article/view?id=43086 (дата обращения: 19.04.2024).