Компетентностный подход предполагает активное использование математических методов и моделей при оценке качества обучения с помощью тестов. Опыт, накопленный во всем мире, показывает, что наряду с совершенствованием самих тестовых материалов, большое влияние на точность и адекватность оценок оказывают методы и модели, используемые для обработки результатов тестирования.
Одной из проблем современного высшего образования, ориентированного на компетентностный подход, является необходимость измерения уровня сформированности нескольких компетенций по результатам оценки качества освоения одной дисциплины, формирующей эти компетенции. Данная проблема следует из требований ФГОС к оценочным материалам и результатам освоения образовательных программ. В настоящее время не существует объективных методов оценки уровня сформированности компетенций на всех этапах их формирования. Как правило, эти оценки производятся на основе экспертных заключений и являются субъективными.
Цель статьи: проверить гипотезу о возможности измерения уровня сформированности нескольких компетенций, исходя из результатов одного сеанса тестирования.
Самой простой и поэтому широко используемой для обработки результатов тестирования является линейная модель. Оценка выполнения задания в ней производится по дихотомической или политомической шкале. Количественным показателем результата тестирования является отношение правильно выполненных к общему количеству предъявленных тестовых заданий (ТЗ).
Данная модель получила наибольшее распространение благодаря простоте и доступности расчетов, а также легкой интерпретации результатов. Недостаток данной модели заключается в том, что она не учитывает полноту и точность ответа и характеристики задания. Она позволяет в какой-то мере оценить уровень знаний обучаемого. Однако по полученным с ее помощью результатам нельзя достоверно определить уровень компетентности.
Широкое распространение в последнее время получили модели, основанные на вероятностных критериях [1]. Такие модели прошли серьезную апробацию при оценке результатов ЕГЭ и в международных исследованиях PISA и TIMMS. Они строятся на утверждении, что вероятность правильного ответа испытуемого зависит от степени его подготовленности и сложности задания. К моделям подобного типа относятся однопараметрическая модель Раша, двух- и трехпараметрическая модель Бирнбаума. Модели данного класса, совокупность которых часто называют современной теорией педагогических измерений (IRT), имеют существенное преимущество по сравнению с другими существующими моделями, так как обеспечивают более высокую точность и объективность оценки достигнутых результатов обучения.
Однако при использовании IRT-моделей в рамках промежуточного или итогового контроля в ходе учебного процесса (данная задача особенно актуальна для российских вузов в связи с требованиями ФГОС) возникают определенные сложности.
Во-первых, классическая модель Раша требует, чтобы вопросы теста относились к одной области знаний, только в этом случае можно корректно оценить уровень подготовленности тестируемых. Компетентностный подход в обучении предполагает, что одна компетенция формируется несколькими дисциплинами, а одна дисциплина может формировать несколько компетенций. Иными словами, в процессе тестирования по дисциплине необходимо измерять уровень сформированности каждой из этих компетенций, что невозможно сделать в рамках классической модели Раша.
Вторая проблема связана с тем, что при проведении промежуточного или итогового контроля по дисциплине не всегда имеется достаточное количество результатов тестирования обучающихся, для того, чтобы провести калибровку теста. Также необходим большой банк тестовых заданий, из которого будут отбираться вопросы, удовлетворяющие требованиям модели Раша [2, 3].
Поэтому в большинстве российских вузов и в популярных системах компьютерного тестирования модель Раша для оценки результатов обучения в ходе учебного процесса не используется. Результаты тестирования измеряются в рамках линейной модели долей успешно выполненных ТЗ и сопоставляются с уровнем сформированности компетенций на основе субъективных экспертных заключений.
Задача ставится следующим образом. Требуется определить уровень сформированности нескольких компетенций в ходе одного сеанса тестирования. При этом желательно использовать имеющиеся банки тестовых заданий, в составе которых присутствуют стандартные дихотомические задания разных типов (открытые, закрытые с одиночным и множественным выбором, на соответствие, на упорядочение) и различной трудности.
Материалы и методы исследования
В основу имитационной модели, построенной в данной работе, положена следующая идея. Для выполнения любого задания в тесте по дисциплине, формирующей несколько компетенций, требуются все эти компетенции, но в разной степени. Первое предположение модели состоит в том, что низкий уровень развития одной компетенции при выполнении задания может компенсироваться высоким уровнем сформированности других компетенций. Например, компетенции УК-1, ОПК-2, ОПК-7, определенные во ФГОС 3++ по направлению 09.03.03 Прикладная информатика [4], формируемые в ходе изучения дисциплин информационного блока, могут проверяться в ходе одного тестирования. При этом задания могут быть успешно выполнены разными методами, с использованием компетенций в области программирования (компетенция ОПК-7), навыков работы в Excel или какого-либо другого специализированного программного обеспечения (компетенция ОПК-2), или использованием навыков поиска и анализа информации (компетенция УК-1).
Для моделирования этого предположения трудность каждого ТЗ задается отдельно для каждой компетенции. Например, если дисциплина формирует три компетенции, то трудность каждого ТЗ задается тремя числами. Уровень сформированности этих компетенций у обучаемого также задается тремя значениями. Тогда вероятность правильного ответа на ТЗ также будет принимать три разных значения.
Второе предположение имитационной модели состоит в том, что поскольку для ответа на вопрос обучаемый старается в максимальной степени использовать все свои компетенции, то вероятность правильного ответа на ТЗ будет равна максимальному значению из всех вероятностей, вычисленных в соответствии с моделью Раша.
Рассмотрим возможность выявления нескольких компетенций по результату одного тестирования на модельном примере. Предположим, что дисциплина формирует три компетенции. Тест, используемый для итогового или промежуточного контроля по дисциплине, должен оценивать уровень обученности студента по каждой компетенции. Предположим также, что каждое задание для своего выполнения требует развития всех трех компетенций, но в разной степени, т.е. каждое задание имеет различный уровень трудности по отношению к разным компетенциям. Например, задание по работе в Excel может быть легким для студента, освоившего работу с современным программным обеспечением, и трудным даже для хорошего программиста. И наоборот, задание, легкое для программиста, может быть трудным для специалиста в области поиска и анализа информации. (Здесь в качестве примера, как и ранее, приводятся компетенции УК-1, ОПК-2, ОПК-7, прописанные в стандарте ФГОС 3++ для направления подготовки «Прикладная информатика» и включаемые в рабочие программы дисциплин цикла «Информационные технологии»).
Обозначим уровни трудности задания по отношению к каждой компетенции t1, t2, t3, а уровни сформированности каждой компетенции у студента С1, С2, С3 соответственно.
В соответствии с двухпараметрической моделью Раша вероятность правильного ответа на вопрос определяется только разностью уровня подготовленности студента и уровня трудности вопроса. В данном случае мы получаем три разные вероятности правильного ответа:
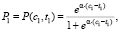 (1)
(1)
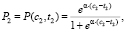 (2)
(2)
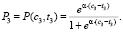 (3)
(3)
При определении вероятности правильного ответа на данный вопрос, который имеет разный уровень трудности по отношению к разным компетенциям и, соответственно, характеризуется тремя значениями вероятности, необходимо, следуя второму предположению модели, выбирать максимальную из этих трех вероятностей.
Следующее предположение, используемое в построенной модели, касается требуемой точности оценки уровней сформированности компетенций. Известно, что точность определения уровня подготовки с помощью тестирования в рамках IRT определяется шагом шкалы оценок трудностей заданий в тесте, т.е. чем меньше шаг и, соответственно, чем больше заданий разной трудности в тесте, тем точнее получаются результаты измерения уровня подготовки. Количество заданий в тесте имеет естественные ограничения и не превышает, как правило, величины в несколько десятков. Использование классической модели Раша при таком количестве заданий позволяет определить уровень подготовленности студента с точностью до десятых долей логита [5].
В рассматриваемой задаче для достижения такой же точности при определении уровня каждой компетенции может потребоваться значительно больше заданий. При этом возникает вопрос: всегда ли нужна высокая точность при измерении уровня подготовленности обучаемого? Несомненно, что высокая точность измерения уровня знаний нужна в процессе ЕГЭ, результаты которого используются в конкурсе при поступлении в вузы. В то же время в большинстве процедур оценивания качества подготовки обучающихся высокая точность не нужна.
Этому утверждению можно дать следующее обоснование. Наши текущие достижения дают вклад в наши будущие успехи на уровне не более 25%. Например, многочисленные лонгитюдные исследования убедительно доказали, что выдающиеся способности, проявившиеся в молодом возрасте, дают вклад в дальнейшую успешность человека на уровне не более 20–25% [6, 7]. Наши исследования взаимосвязи результатов ЕГЭ по математике с дальнейшим успешным ее изучением в вузе также подтвердили подобный вывод [8]. В полной мере это относится и к процедурам промежуточного и итогового контроля в процессе обучения. Как правило, для оценки в этом случае используются четыре градации (неудовлетворительно, удовлетворительно, хорошо, отлично) или два значения (зачет, незачет). Неслучайно во вкладыше диплома о высшем образовании встречаются только три оценки.
Таким образом, в большинстве случаев нет смысла очень точно измерять текущий уровень подготовки студента. Гораздо важнее не точность поставленной оценки, а объективность результатов оценивания обученности студентов.
Третье предположение, на основе которого построена имитационная модель, состоит в том, что уровень сформированности каждой компетенции оценивается по четырехбалльной шкале. Это предположение обуславливает появление дополнительной ошибки квантования, которая в данном случае примерно равна 0,3 балла и имеет аддитивный характер.
Результаты исследования и их обсуждение
Для проверки гипотезы о возможности оценки уровня подготовленности обучающегося по трем компетенциям на основе анализа результатов одного тестирования предлагается следующий алгоритм.
Установим следующее соответствие между используемой шкалой оценивания и уровнем развития компетенций в логитах: отлично – 3, хорошо – 1, удовлетворительно – минус 1 и неудовлетворительно – минус 3. В случае одновременного оценивания трех компетенций возможны 64 уникальные комбинации уровней их сформированности по такой четырехбалльной шкале, что будет соответствовать 64 типам студентов. Предполагается, что удалось сформировать банк тестовых заданий, уровни трудности которых относительно каждой компетенции меняются с тем же шагом по шкале трудностей. Таким образом, в имитационной модели рассматриваются 64 уникальных комбинации значений трудности заданий для трех компетенций и 64 условных типа студента с разными комбинациями обученности по этим компетенциям.
В таблице показан фрагмент матрицы вероятностей правильного ответа на каждый из вариантов вопросов студентами различных типов. Каждая строка матрицы соответствует одному типу вопроса теста, каждый столбец – уникальному набору уровней сформированности компетенций.
Вероятности, приведенные в данной матрице, рассчитываются по формуле
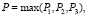 (4)
(4)
где P1, P2, P3 вычисляются по формулам (1)–(3).
Значения информационной функции задания вычисляются как сумма произведений вероятности правильного и неправильного ответа на данное задание по всем типам студентов:
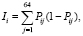
где Pij – вероятность правильного ответа j-го типа студента на i-й тип вопроса. Вопросы в таблице отсортированы в порядке убывания информационной функции с целью дальнейшего отбора нужного количества информативных тестовых заданий.
Матрица вероятностей правильных ответов (матрица прототипов)
|
Типы студентов с уникальным набором компетенций (условный номер типа студента и три значения уровня его компетенций в логитах) |
||||||||||||||
|
Список типов заданий. Трудность по каждой компетенции, логит |
1 |
2 |
3 |
4 |
… |
… |
… |
61 |
62 |
63 |
64 |
Значение информационной функции задания |
||
|
3 |
3 |
3 |
3 |
… |
… |
… |
-3 |
-3 |
-3 |
-3 |
||||
|
3 |
3 |
3 |
3 |
… |
… |
… |
-3 |
-3 |
-3 |
-3 |
||||
|
3 |
1 |
-1 |
-3 |
… |
… |
… |
-3 |
3 |
1 |
-1 |
||||
|
t1 |
t2 |
t3 |
Вероятности успешного выполнения задания |
|||||||||||
|
3 |
3 |
3 |
0,500 |
0,500 |
0,500 |
0,500 |
… |
… |
… |
0,000 |
0,500 |
0,032 |
0,001 |
9,852 |
|
3 |
1 |
3 |
0,968 |
0,968 |
0,968 |
0,968 |
… |
… |
… |
0,001 |
0,500 |
0,032 |
0,001 |
8,442 |
|
1 |
3 |
3 |
0,968 |
0,968 |
0,968 |
0,968 |
… |
… |
… |
0,001 |
0,500 |
0,032 |
0,001 |
8,442 |
|
3 |
3 |
1 |
0,968 |
0,500 |
0,500 |
0,500 |
… |
… |
… |
0,001 |
0,968 |
0,500 |
0,032 |
8,442 |
|
3 |
1 |
1 |
0,968 |
0,968 |
0,968 |
0,968 |
… |
… |
… |
0,001 |
0,968 |
0,500 |
0,032 |
7,190 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
-3 |
1 |
-3 |
1,000 |
1,000 |
1,000 |
1,000 |
… |
… |
… |
0,500 |
1,000 |
0,999 |
0,968 |
1,180 |
|
-3 |
-3 |
1 |
1,000 |
1,000 |
1,000 |
1,000 |
… |
… |
… |
0,500 |
0,968 |
0,500 |
0,500 |
1,180 |
|
-1 |
-3 |
-3 |
1,000 |
1,000 |
1,000 |
1,000 |
… |
… |
… |
0,500 |
1,000 |
0,999 |
0,968 |
0,840 |
|
-3 |
-1 |
-3 |
1,000 |
1,000 |
1,000 |
1,000 |
… |
… |
… |
0,500 |
1,000 |
0,999 |
0,968 |
0,840 |
|
-3 |
-3 |
-1 |
1,000 |
1,000 |
1,000 |
1,000 |
… |
… |
… |
0,500 |
0,999 |
0,968 |
0,500 |
0,840 |
|
-3 |
-3 |
-3 |
1,000 |
1,000 |
1,000 |
1,000 |
… |
… |
… |
0,500 |
1,000 |
0,999 |
0,968 |
0,491 |
Для более точного определения уровня сформированности компетенций необходимо, чтобы вопросы теста обладали наибольшей информативностью. С другой стороны, они должны одинаково надежно определять уровень сформированности компетенций у студентов с различными комбинациями их значений, т.е. их трудности должны равномерно перекрывать весь диапазон уровней подготовленности студентов.
Из анализа таблицы следует, что наиболее информативными являются ТЗ, имеющие максимальную трудность по всем компетенциям, кроме одной. Если включить в тест все 64 типа вопросов, то такой тест будет малоинформативным. Действительно, в соответствии с нашим вторым предположением о максимальной вероятности правильного ответа, большинство студентов, относящихся к разным типам, будут правильно отвечать на большую часть вопросов такого теста.
Поскольку реальные тесты, как правило, включают не менее 20 вопросов, составим тест из 26 наиболее информативных вопросов, трудности которых равномерно распределены по всему диапазону уровней подготовленности студентов.
Измерения уровней подготовленности студентов основаны на использовании функции правдоподобия. Пусть у нас имеется студент с неизвестными значениями уровней сформированности компетенций C1, C2, C3. Сопоставим набор ответов студента с матрицей вероятностей правильных ответов и выберем столбец матрицы с наиболее «правдоподобной» комбинацией значений C1*, C2*, C3*. Для этого рассчитаем значение функции правдоподобия Lj для каждого j-го столбца по следующему правилу:
 (5)
(5)
Столбец, обеспечивающий максимум Lj, определяет «тип» студента. Припишем тестируемому студенту уровни подготовленности, соответствующие этому прототипу.
Для оценки адекватности предлагаемого алгоритма проведем следующий имитационный эксперимент. Зададим для студента некоторые значения уровней сформированности каждой из трех компетенций C1, C2, C3. Для каждого i-го задания, используя соотношения (1)–(3), вычислим вероятности P1, P2, P3 и по формуле (4) рассчитаем вероятность (Pi) того, что студент справится с этим заданием. В результате получим вектор вероятностей правильных ответов на вопросы теста для данного студента. Далее, на основе этого вектора вероятностей, формируем вектор ответов студента, содержащий нули и единицы, пользуясь следующим алгоритмом. Генерируем случайные числа ri, равномерно распределенные в диапазоне [0, 1]. Если значение ri меньше величины Pi, то записываем i-м значением вектора ответов единицу и ноль в противном случае.
Методом максимального правдоподобия определим тип данного студента, т.е. установим измеренные значения уровней сформированности его компетенций C1*, C2*, C3* на дискретной шкале, содержащей по четыре градации для каждой компетенции.
Мерой точности проведенного измерения будем считать среднеквадратическое отклонение измеренного значения от истинного в серии подобных измерений. Серию измерений организуем, формируя случайным образом, на основе одного и того же вектора вероятностей правильных ответов студента на вопросы теста, различные векторы ответов студента.
Серия измерений в имитационном эксперименте включала 200 вариантов ответов студента, полученных из одного вектора вероятностей его правильных ответов. На рис. 1 показано, как зависит стандартное отклонение при измерении величины C3 от значения C3 при фиксированных значениях C1, C2.
Кривая (С2 = -3) подтверждает тот факт, что максимальная ошибка измерения в полбалла (?3 ? 1 логит) наблюдается при оценке студентов, уровень подготовленности которых соответствует середине промежутков между делениями шкалы оценок (-2 логита, 0 логитов, +2 логита). Это хорошо проявляется, когда две другие компетенции оказываются плохо сформированными (кривая С2 = -3). Наибольшая ошибка наблюдается, когда измеряется низкое значение С3 на фоне высокого значения С2 (кривая С2 = 3).
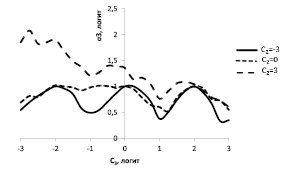
Рис. 1. Стандартное отклонение при измерении величины C3 при фиксированных значениях C1, C2. (С1 = -3)
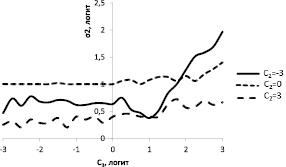
Рис. 2. Стандартное отклонение при измерении величины C2 при фиксированных значениях C1, C2. (С1 = -3)
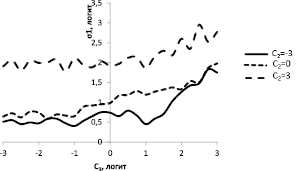
Рис. 3. Стандартное отклонение при измерении величины C1 при фиксированных значениях C1, C2. (С1 = - 3)
На рис. 2 показано, как зависит стандартное отклонение при измерении величины C2 от значения C3 при фиксированных значениях C1, C2.
Кривые, приведенные на рисунке, также подтверждают, что наибольшая ошибка наблюдается, когда измеряется низкое значение С2 на фоне высокого значения С3 (кривая С2 = -3).
Наихудшие условия для измерения уровня компетентности возникают тогда, когда мы пытаемся измерить низкий уровень сформированности одной компетенции на фоне высокого развития двух других компетенций. Ошибки этого варианта измерений показаны на рис. 3, где приведены результаты измерения величины C1, имеющей фиксированное значение -3 логита.
Стандартное отклонение в этом наихудшем случае (кривая С2 = 3) может достигать значений в один балл (?1 ? 2 логит). При этом измерение будет давать завышенный результат уровня компетенции, имеющей низкое значение на фоне высоких значений других компетенций.
Выводы
Из результатов численного эксперимента, проведенного на имитационной модели, видно, что предлагаемая методика позволяет оценить степень сформированности каждой из трех компетенций по результатам одного тестирования, включающего несколько десятков заданий. Однако точность оценки сильно зависит от соотношения уровней различных компетенций у студента. Наибольшая погрешность, мерой которой является стандартное отклонение измеренной величины, наблюдается в случаях, когда измеряется низкий уровень развития одной компетенции на фоне высокого уровня развития других компетенций. Для студентов, имеющих средние уровни подготовки по каждой компетенции, погрешности оценок не превышают значения 1 логит, что соответствует приблизительно половине балла при четырехбалльной шкале оценивания. Такую погрешность можно считать приемлемой для промежуточного и итогового контроля.
Предложенный подход использует в некоторой степени идею работы [9], где для оценки также используются заранее определенные классы тестируемых (паттерны). Его можно рассматривать как расширение классической IRT. Использование для оценки всей совокупности ответов испытуемого делает данную методику менее подверженной влиянию случайных факторов, по сравнению с моделью Раша, где оценка выставляется на основе результатов выполнения заданий с приблизительно равными вероятностями правильного и неправильного ответов, что делает результаты тестирования зависимыми от посторонних случайных факторов, не связанных с измеряемыми величинами. Кроме этого, предложенный подход хорошо сочетается с методиками адаптивного тестирования, так как он позволяет на некотором подмножестве вопросов установить тип студента и затем уточнить его характеристики с помощью дополнительных вопросов.
Методика, базирующаяся на предлагаемой концепции, дает возможность объективной оценки уровней сформированности нескольких компетенций по результатам одного тестирования с точностью, приемлемой для текущего и итогового контроля.
Полная, объективная и актуальная информация об уровне сформированности компетенций, которая может быть получена по результатам промежуточного и итогового тестирования обучающихся, позволит повысить адекватность и качество оперативного управления учебным процессом.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-013-00783.
Библиографическая ссылка
Соколова Т.Н., Гусятников В.Н., Безруков А.И., Каюкова И.В. МЕТОДИКА ОЦЕНКИ НАБОРА КОМПЕТЕНЦИЙ НА ОСНОВЕ РЕЗУЛЬТАТОВ ТЕСТИРОВАНИЯ // Фундаментальные исследования. 2020. № 12. С. 209-215;URL: https://fundamental-research.ru/ru/article/view?id=42935 (дата обращения: 06.03.2026).
DOI: https://doi.org/10.17513/fr.42935



