Экономическая безопасность региона является интегральным отображением состояния экономики региона и, естественно, разные ее аспекты обусловлены материальными носителями, с которых отображено само понятие экономика региона. К таковым можно отнести: кадровый потенциал, запасы полезных ископаемых и природных ресурсов, промышленный и агропотенциал, сбалансированность регионального бюджета и др. Сюда же добавляется еще и состояние системы управления регионом, а именно, ее способность мобилизовать перечисленные составляющие к противостоянию любым экономическим угрозам.
Чем выше уровни благополучия указанных основных составляющих системы экономической безопасности региона, тем выше привлекательность этого региона для инвестиций, выше уровень жизни населения. Вследствие этого регион повышает ресурсы, которые можно направить на повышение уровня экономической безопасности. При этом понятно, что вкладывать их надо не «размазывая» равномерно, а кумулятивно, с наилучшими результатами. Проведем, в связи с этим, системный анализ затронутых вопросов.
Экономическая безопасность является абстрактным объектом и не допускает реальных управляющих воздействий на нее, а так же непосредственных измерений для оценки результатов этих воздействий [1], поэтому она делает систему управления иерархической и занимает верхний уровень, как представлено на рис. 1.
Уровень экономической безопасности региона обычно оценивается интегрально [2, 3] по многим показателям: уровню прибыльности предприятий на территории региона, уровню имеющихся запасов и активов, физической и информационной защищенности интересов региона, развитию страхования, привлекательности инвестирования, уровню жизни населения, отлаженностью многочисленных юридических сторон деятельности на территории региона и так далее.
С другой стороны, можно выделить три важных аспекта: оценка результатов текущего мониторинга состояния экономики и прогноз ближайших экономических угроз, а также мониторинг текущего уровня готовности региона к их отражению. К осложняющим обстоятельствам в настоящее время можно отнести многие факторы, в частности, быструю цифровизацию экономики, которая придает ей большую динамику, но многократно увеличивает число экономических угроз [4, 5].
В таких условиях с точки зрения экономической безопасности главным свойством составляющих ее систем должна стать готовность к отражению экономических угроз, поэтому она располагается на втором уровне иерархии. Оценка ее уровня может проводится тестовыми процедурами, отработанными на результат. Это позволяет гарантировать определенный уровень точности.
Первый уровень управления образуют пять основных составляющих систем, перечисленных выше. При этом в систему управления включено и прогнозирование экономических угроз. Это позволит более точно и адаптивно распределять управляющие ресурсы на повышение уровней готовности составляющих систем, поддерживая оптимальный уровень их готовности к текущему моменту. Понятно, что с верхнего уровня должны поступать укрупненные и довольно глубокие воздействия, а не мелкие и дублирующие нижние функции управления. Сюда относятся: задание принципиальных значений ключевых параметров (параметрические воздействия), структурные изменения как технологических частей составляющих системы экономической безопасности, так и подсистем управления ими (структурные воздействия), а так же организационные изменения, имеющие целью создание благоприятных условий поддержания должного уровня экономической безопасности.
Примем гипотезу, что вероятность появления экономической угрозы имеет марковскую природу. Марковские модели, как первое приближение в описании случайных процессов, довольно часто применяются в экономике: при исследовании тайваньских бизнес-циклов [6], в управлении цепями поставок [7], в формировании спроса на кредиты [8], для анализа долгосрочных свойств акций и дивидендов в США [9], в моделировании процесса формирования цены [10]. Достоинством такого подхода является возможность описания процессов уравнением Колмогорова:
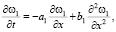 (1)
(1)
где a1 – коэффициент сноса; b1 – коэффициент диффузии, ω1 – плотность описанной выше вероятности, зависящая от времени и какого-либо интегрального показателя x, специфичного именно для данного региона. Это может быть валютный курс или индекс фондовой биржи [11], если существуют обширные контакты с международным рынком, биржевой индекс отечественной фирмы, имеющей инвестиции на местном рынке и так далее.
Уравнение (1) может быть решено с использованием функции Грина [12]. Однако сначала его необходимо привести к каноническому виду
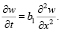 (2)
(2)
Осуществляется это с помощью подстановки:
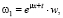 при
при 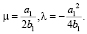 (3)
(3)
При начальном условии
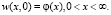 (4)
(4)
И граничном условии
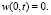 (5)
(5)
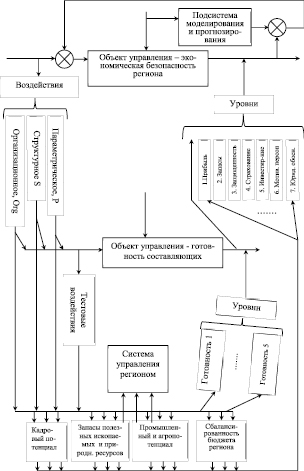
Рис. 1. Трехуровневая схема управления уровнем экономической безопасности предприятия
Тогда решение уравнения (1) представляется в виде [4, c. 236]
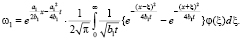 (6)
(6)
Готовность региона отразить возникшую угрозу будем оценивать уровнем вероятности ее успешного отражения и, в первом приближении, для адекватной реакции региона, последняя должна подчиняться похожему на (1) уравнению с добавлением в правой части управляющего воздействия u(x, t) [12]. При этом плотность вероятности обозначается ω2 и зависит от тех же параметров, что и вероятность из уравнения (1):
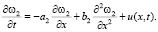 (7)
(7)
Прологарифмировав уравнения (1) и (7) и вычитая из первого уравнения второе, получим уравнение в частных производных от величины
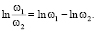 (8)
(8)
Эта величина равна единице, только в случае равенства, входящих в нее плотностей вероятности и может быть положительной в случае превосходства ω2 и отрицательной в противоположном случае. Такое представление удобно в случае принятия гипотезы о том, что плотность вероятности готовности региона складывается из плотностей вероятностей готовности составляющих его системы экономической безопасности, как независимых друг от друга. Тогда плотность вероятности готовности региона равна произведению плотностей вероятности готовностей составляющих, перечисленных выше и формула (8) представляется в следующем виде
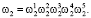 (9)
(9)
Примем так же гипотезу о том, что, в первом приближении, все пять составляющих по обеспечению необходимого уровня системы экономической безопасности подчиняются уравнению Колмогорова.
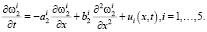 (10)
(10)
А формула (8) преобразуется к следующему виду
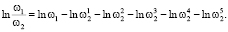 (11)
(11)
Для нахождения соответствующих управляющих воздействий воспользуемся функционалом, включающем потери от неоптимального управления в виде вышеописанного логарифма, с одной стороны, и затраты на управление с другой.
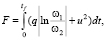 (12)
(12)
где q – размерный весовой коэффициент.
Как видим, здесь подинтегральная функция видоизменена по сравнению с квадратичными потерями в классическом случае выбрано слагаемое в виде описанного выше логарифма отношения двух вероятностей.
Применим для решения данной задачи метод Эйлера-Лагранжа. Построим лагранжиан
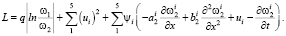 (13)
(13)
На практике управляющие воздействия направлены на повышение уровней вероятности успешного отражения угроз составляющими, а снижение этой вероятности происходит естественным образом в силу релаксационности происходящих вероятностных процессов, описываемых уравнениями (10). Это означает, что знак абсолютной величины в уравнении (13) можно опустить.
Составляем уравнения Эйлера по всем переменным:
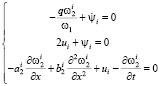 i = 1, …, 5. (14)
i = 1, …, 5. (14)
Подстановка ψi из второго уравнения этой системы в первое дает:
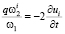 или
или 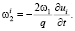 (15)
(15)
Подставляем полученное выражение в третье уравнение системы (14):
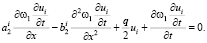 (16)
(16)
Выполняя дифференцирование получим
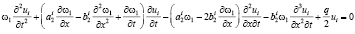 i = 1,…,5. (17)
i = 1,…,5. (17)
Замечаем, если уравнения, описывающие вероятностные процессы возникновения угроз и формирования уровня готовности к их отражению имеют одинаковые коэффициенты сноса и диффузии, второе слагаемое пропадает.
Воспользуемся методом разделения переменных, для чего представим управляющее воздействие в виде произведения двух функций
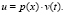 (18)
(18)
Подставляя это выражение в (21) получим:
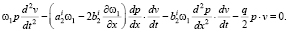 (19)
(19)
Разделив обе части (18) на 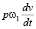 имеем
имеем
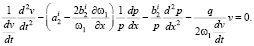 (20)
(20)
Учитывая, что ω1 мы можем определить по (6), разделяем переменные
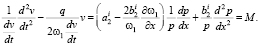 (21)
(21)
Таким образом, решение уравнения (20) сводится к решению системы двух уравнений
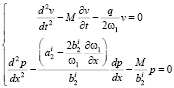 (22)
(22)
По своей структуре эти уравнения подобны, полученным в работе [13]. Их решение выражается через экспоненты и при фиксированных значениях ω1 отражается в соответствии с графиками, приведенными на рис. 2.
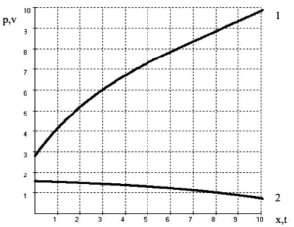
Рис. 2. Изменения составляющих управляющего воздействия: 1 – p(x); 2 – v(t)
Однако есть и весьма существенное отличие от результатов работы [13], поскольку в явном виде выражена зависимость коэффициентов в уравнении, определяющем величину оптимальных управляющих воздействий, от поведения вероятности возникновения экономических угроз. Это, в свою очередь, позволит проводить более тонкий анализ взаимосвязей описываемых экономических процессов.
Заключение
Таким образом, системный анализ управления уровнем экономической безопасности региона позволил установить значительную специфику осуществляемых управленческих процедур, связанных с формированием оценки уровней управляемых величин и интеграцией управляющих воздействий. Удобство выделения уровней управления связано с непересекаемостью достигаемых целей и, следовательно, четким разделением затрат управляющих ресурсов, направляемых на их достижение. Разработанная методика перераспределения управляющих ресурсов позволяет максимизировать уровень экономической безопасности даже при малых ресурсах. Исследование ограничивается основными составляющими, но разработанная методика универсальна и допускает большую детализацию.
Библиографическая ссылка
Пищухин А.М., Ахмедьянова Г.Ф. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭКОНОМИЧЕСКОЙ БЕЗОПАСНОСТЬЮ РЕГИОНА // Фундаментальные исследования. 2020. № 12. С. 180-185;URL: https://fundamental-research.ru/ru/article/view?id=42930 (дата обращения: 31.01.2026).
DOI: https://doi.org/10.17513/fr.42930



