Целью работы является нахождение оптимального пути в графе, веса ребер которого изначально известны с определенной вероятностью, за ограниченное время, с условием возвращения в точку начала движения.
В соответствии с целью работы были сформулированы следующие основные задачи:
1. реализация поиска оптимального пути на каком-либо языке программирования;
2. в нашем случае понятие оптимального пути включает в себя не только поиск кратчайшего пути, но и обход вершин с максимальными весами;
3. применение алгоритма Дейкстры и усовершенствование этого алгоритма в плане временного ограничения, а также дополнение его условием возвращения в точку начала движения;
4. добавление в программу функции графического изображения.
Практическая значимость работы подтверждается возможностью использования данного проекта в следующих сферах.
1. Рогейн или спортивное ориентирование. При ограниченных возможностях участника (он или перемещается, или разрабатывает оптимальный маршрут) и неопределенности состояния трассы проект дает возможность провести имитационное моделирование прохождения дистанции и статистическими методами построить оптимальную стратегию.
2. Схема движения дежурного транспорта предприятия. Появляется возможность составления оптимального графика движения с учетом величины и вероятности задержек дежурной бригады на осматриваемых объектах. Аналогичной является задача осмотра объектов экипажем службы безопасности при визуальной охране.
3. План распределения машин по мере поступления заявок в таксопарке, с учетом местонахождения такси. Вероятность поступления заявок на перевозки, определяемая распределением населения по территории города, наличием и циклами суточной активности посещаемых объектов, позволяет на основе результатов имитационного моделирования перевозок динамически распределять свободные машины такси по городу, чтобы минимизировать их простои.
Из дискретной математики, в частности, теории графов, известны следующие аналоги задачи, для которых разработаны методы решения:
- задача о Кенигсбергских мостах;
- задача о трех домах и трех колодцах;
- задача о четырех красках.
Граф представляет собой множество точек плоскости 
, называемых вершинами, и множество направленных отрезков 
, соединяющих все или некоторые из вершин и называемых дугами. Математически граф 
можно определить как пару множеств и :
.
Т.к. в нашей задаче из каждой вершины можно попасть во все другие, то граф является полным.
Маршрутом в графе называется чередующаяся последовательность вершин и ребер
v0, e1, v1,e2, v2, …, ek, vk,
в которых любые два соседних элементов инцидентны. Маршрут в нашем графе должен быть замкнутым, т.е. v0 = vk – выполняется условие возвращения в точку начала движения.
Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведем наиболее часто используемых представлений с указанием характеристики n(p,q) – объема памяти для каждого представления p, (q – число ребер):
- представление графа с помощью квадратной булевой матрицы M : array [1..p, 1..p] of 0..1, отражающей смежности вершин, которая называется матрицей смежности, для которойn(p,q)=O(p2).
- представление графа с помощью матрицы инциденций, для которой n(p,q)=O(p× q).
- представление графа с помощью списка смежности, причем для ориентированных графов n(p,q)=O(p+q).
- представление графа с помощью массива дуг и для массива ребер (или дуг), n(p,q)=O(2q).
Обход графа – это некоторое систематическое перечисление его вершин (и/или ребер). Длиной пути называется сумма длин дуг, входящих в этот путь. Наиболее часто на практике встает задача отыскания кратчайшего пути. Существуют два классических алгоритма ее решения.
Алгоритм Флойда находит все кратчайшие пути между всеми парами вершин в (ор) графе. В этом алгоритме для хранения информации о двух путях используется матрица
H[1..p, 1..p],
где 
: k – если k – первая вершина, достигаемая на кратчайшем пути из i в j; 0, если пути из i в j нет.
Вход: матрица C[1..p,1..p] длин дуг.
Выход: матрица Т[1..p,1..p] длин путей и матрица H[1..p,1..p] самих путей.
for i from 1 to p do
for j from 1 to p do
T[i,j]:= C[i,j] { инициализация }
if C[i,j] = ∞ then
H[i,j]:= 0 { нет дуги из i в j }
else
H[i,j]:= j { есть дуга из i в j }
end if
end for
end for
for i from 1 to p do
for j from 1 to p do
for k from 1 to p do
if i≠j&T[j,i]≠∞&i≠k&T[i,k]≠∞&(T[j,k]=∞VT[j,k]>T[j,i]+T[i,k])
then
H[j,k]:=H[j,i] { запомнить новый путь }
T[j,k]:=T[j,i]+T[i,k] { и его длину }
end if
end for
end for
for j from 1 to p do
if T[j,j]<0 then
stop { нет решения: вершина j входит в цикл отрицательной длины }
end if
end for
end for
Алгоритм Дейкстры находит кратчайший путь между двумя данными вершинами в (ор) графе, если длины дуг неотрицательны.
Вход: орграф G(V,E), заданный матрицей дуг С:array[1..p,1..p] of real; s и t – вершины графа.
Выход: векторы T:array[1..p] of real; и H:array[1..p] of 0..p. Если вершина v лежит на кратчайшем пути от s к t, то T[v] – длина кратчайшего пути от s к v; H[v] – вершина, непосредственно предшествующая v на кратчайшем пути.
for v from 1 to p do
T[v]:=∞ { кратчайший путь неизвестен }
X[v]:=0 { все вершины не отмечены }
end for
H[s]:=0 {s ничего не предшествует }
T[s]:=0 { кратчайший путь имеет длину 0…}
X[s]:=1 {… и он известен }
v:=s { текущая вершина }
M: { обновление пометок }
for u
Г(v) do
if X[u]=0&T[u]>T[v]+C[v,u] then
T[u]:=T[v]+C[v,u] { найден более короткий путь из s в u через v }
H[u]:=v { запоминаем его }
end if
end for
t:= ∞; v:=0
{ поиск конца кратчайшего пути }
for u from 1 to p do
if X[u]=0&T[u]<t then
v:=u;t:=T[u] {вершина v заканчивает кратчайший путь из S }
end if
end for
if v=0 then
stop { нет пути из s в t}
end if
if v=t then stop { найден кратчайший путь из s в t }
end if
X[v]:=1 { найден кратчайший путь из s в v }
goto M
В настоящее время в среде Borland C++ Builder 6 реализован (рис. 1) алгоритм поиска кратчайшего пути в графе, веса ребер которого заранее известны с определенной вероятностью. Исходными данными является массив расстояний между парами вершин графа (весов ребер), массив вариаций весов и стоимость вершин.
Путем имитационного моделирования определяется оптимальный путь обхода. Для обхода применяется вариант алгоритма Дейкстры, в котором реальный вес всех ребр, инцидентных вершине, определяется в момент прихода в вершину с учетом их начального веса и пределов стохастической неопределенности весов. Критерием оптимальности является соотношение весов пройденных ребер к стоимости вершин, задачей оптимизации его минимизация. Таким образом, достигается эффективность в смысле прохождения наибольшей суммы вершин за минимальное (или ограниченное) время, находящееся в корреляции с весом ребра.
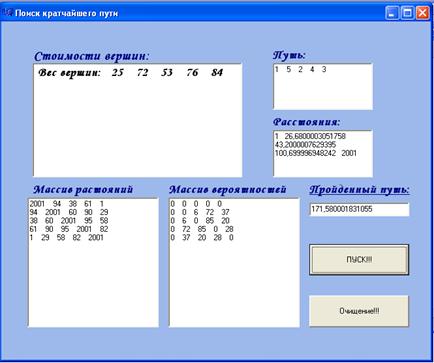
Рис. 1. Главная форма программы
Дальнейшая разработка заключается в дополнении программы временными ограничениями и другими необходимыми условиями, а также графическим изображением графа с выделенным оптимальным путем.
Библиографическая ссылка
Пастухова Ю.Г., Фатеева Т.А., Затонский А.В. ПОИСК ОПТИМАЛЬНОГО ПУТИ В ДИНАМИЧЕСКИ ИЗМЕНЯЮЩЕМСЯ ГРАФЕ // Фундаментальные исследования. – 2007. – № 12-3. – С. 435-438;URL: https://fundamental-research.ru/ru/article/view?id=4292 (дата обращения: 15.10.2024).