Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Тырсин А.Н. 1, 2 Васильева Е.В. 3

---

1 ФГАОУ ВО «Уральский федеральный университет имени Первого Президента России Б.Н. Ельцина»

2 ФГБУН «Научно-инженерный центр «Надежность и ресурс больших систем и машин» УрО РАН

3 ФГБУН «Институт экономики» УрО РАН

Бинарная логистическая регрессия – известный метод многомерного статистического анализа, используемый для классификации данных. В экономических задачах возникают ситуации, когда необходимо расширить ее область применения и использовать в задачах мониторинга и выработки управленческих решений. Для количественной характеристики качества жизни населения использован широко распространенный показатель – индекс человеческого развития. Целью статьи является разработка инструментария для использования бинарной логистической регрессии в задачах диагностики и управления многомерными системами и его апробация применительно к вопросам увеличения индекса человеческого развития регионов России. Описана математическая модель мониторинга и управления многомерными стохастическими системами, построенная на основе бинарной логистической регрессии. Бинарная логистическая регрессия как модель мониторинга и управления апробирована на примере задачи повышения качества жизни регионов. В качестве вектора исходных данных использован набор социально-экономических показателей регионов России. Описан подход к выработке управленческих решений для региона в виде оптимизационных задач увеличения вероятности отнесения его к классу регионов с высоким уровнем качества жизни. На основе выявленной взаимосвязи между качеством жизни населения и социально-экономическими показателями региона решена задача оптимизации.

Статья в формате PDF

0 KB

бинарная логическая регрессия

оптимизационная задача

качество жизни

индекс человеческого развития

социально-экономические показатели

регион

1. Попова П.А., Ротмистров А.Н. Логистическая регрессия с категориальными предикторами и эффектами взаимодействия и CHAID: сравнительный анализ на эмпирическом примере // Социология: 4М. 2016. № 43. С. 63–99.

2. Кацов И. Машинное обучение для бизнеса и маркетинга. СПб.: Питер. 2019. 512 с.

3. Hosmer D.W., Lemeshow S., Sturdivant R.X. Applied Logistic Regression. 3d ed. Wiley. 2013. 397 p.

4. Воронцов К.В. Лекции по алгоритмам восстановления регрессии. 2007. [Электронный ресурс]. URL: http://www.ccas.ru/voron/download/Regression.pdf (дата обращения: 15.09.2020).

5. Hilbe J.M. Logistic Regression Models. CRC Press. 2009. 656 p.

6. Пантелеев А.В., Летова Т.А. Теория оптимизации для инженеров и экономистов. М.: Вузовская книга, 2016. 568 с.

7. Васильев Н.П., Егоров А.А. Опыт расчета параметров логистической регрессии методом Ньютона–Рафсона для оценки зимостойкости растений // Математическая биология и биоинформатика. 2011. Т. 6. № 2. С. 190–199. [Электронный ресурс]. URL URL: http://www.matbio.org/article_pdf.php?id=82 (дата обращения: 15.09.2020).

8. Тырсин А.Н., Костин К.К. Оценивание логистической регрессии как экстремальная задача // Вестник Томского государственного университета. Управление, вычислительная техника и информатика. 2017. № 3(40). С. 52–60. DOI: 10.17223/19988605/40/6.

9. Баева О.Н. Индекс человеческого развития: методики определения и оценки на уровне региона // Известия Иркутской государственной экономической академии (Байкальский государственный университет экономики и права). 2012. № 5. С. 143–147.

10. Тырсин А.Н., Чистова Е.В., Костин К.К. Моделирование взаимосвязи между качеством жизни и социально-экономическими показателями регионов России // Государственное управление. Электронный вестник. 2016. № 59. С. 212–237.

11. Кейнс Дж.М. Общая теория занятости, процента и денег: Пер. с англ. М.: ЗАО «Бизнеском», 2013. 402 с.

12. Чурилова Е. Анализ взаимозависимости уровня рождаемости и индекс развития человеческого потенциала. Презентация доклада. Демоскоп Weekly, № 399–400. 23 ноября – 6 декабря 2009. [Электронный ресурс]. URL: http://www.demoscope.ru/weekly/2009/0399/student02.php (дата обращения: 15.09.2020).

Бинарная логистическая регрессия – известный метод многомерного статистического анализа, используемый для классификации данных в экономике [1; 2]. Она осуществляет разделение множества многомерных данных линейной границей на соответствующие заданным классам две области и прогнозирует вероятность соответствия каждой точки этим классам [3].

Достаточно часто, особенно в малоизученных приложениях, возникают ситуации, когда не удается построить качественную линейную регрессионную зависимость даже с учетом использования замен переменных. Основная причина этого состоит в неполноте модели из-за отсутствия части существенных переменных. Также существенных переменных может оказаться очень много, но они проявляются лишь эпизодически при наступлении некоторых условий и в регрессионной модели будут статистически не значимыми.

В этой ситуации причинно-следственную математическую модель можно построить на основе логистической регрессии, которая не накладывает жестких условий на переменные. Здесь лишь требуется суметь разделить наблюдения на две группы, что является значительно более простой процедурой. Затруднение, связанное с непрерывностью зависимой переменной Y, преодолимо с помощью формирования значений новой бинарной величины 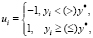где y* – некоторое пороговое значение. Но применение логистической регрессии только как классификатора будет недостаточным, необходим инструментарий для ее использования для диагностики и управления.

Рассмотрим иное возможное использование бинарной логистической регрессии как замены в некотором смысле модели линейной регрессии. Целью статьи является разработка инструментария для использования бинарной логистической регрессии в задачах мониторинга и выработки управленческих решений многомерными стохастическими системами и его апробация применительно к вопросам увеличения индекса человеческого развития регионов России. Исходные данные взяты из справочников Росстата.

Материалы и методы исследования

Дана выборка прецедентов (обучающая выборка) значений признаков X1, X2, ..., Xm

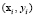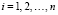, , (1)

где 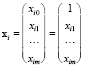– вектор значений i-го объекта, 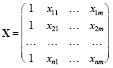; 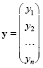, 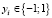– указывающая на принадлежность i-го объекта соответствующему классу бинарная переменная (для первого класса yi = –1, для второго – yi = 1); m – количество признаков у объектов; n – число наблюдений.

Классификация выполняется с помощью логистической функции [3]

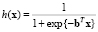, (2)

причем 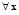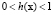. Вектор 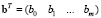является набором коэффициентов, задающих разделяющую границу, которая представляет собой гиперплоскость

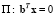. (3)

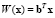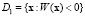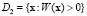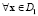
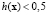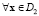
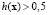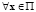
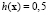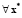
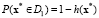Введем функцию . Зададим область D1 возможных значений x для первого класса как , а для второго класса – как . Тогда , , и и 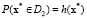. Если 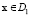, то y = –1, в противном случае y = 1.

В [4] предложен метод вычисления коэффициентов вектора b с помощью решения задачи

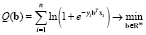. (4)

Вектор коэффициентов b оценивают разными алгоритмами, например используют алгоритм Ньютона–Рафсона [4–6]. Однако при корректной классификации всех наблюдений целевая функция Q(b) имеет нулевую нижнюю грань на бесконечности, и поэтому задача (4) не будет иметь точного решения. Увеличение компонент вектора b вызывает неограниченный рост некоторых значений 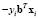. В результате этого происходит рост вычислительных погрешностей, приводящий к переполнению памяти и к остановке алгоритма [7].

В [8] описан алгоритм нулевого порядка, использующий на каждой итерации случайный поиск с фиксацией длины вектора b. Это позволяет устранить неконтролируемый рост вычислительных погрешностей и обеспечивает устойчивость работы алгоритма.

Рассмотрим задачу классификации регионов по качеству жизни населения на два класса. Используем данные за 2013 г., так как это последний год перед усложнением внешнеполитической (ведение санкций против России из-за присоединения Крыма) и внешнеэкономической (падение цен на нефть) обстановки. Для численной оценки качества жизни населения регионов используем индекс человеческого развития (ИЧР) [9]. В качестве компонент вектора x будем использовать набор социально-экономических показателей регионов России. Регионы разделим на два класса, к первому классу D1 отнесем регионы с низким ИЧР (y = –1), а ко второму классу D2 – с высоким ИЧР (y = 1). Это разделение описано в [10].

Будем использовать вероятность 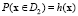отнесения региона к классу D2 как целевую функцию. Фактически это означает, что мы стремимся повысить качество жизни населения региона посредством выработки и реализации управленческих рекомендаций, повышающих вероятность h(x) его отнесения к классу регионов с высоким ИЧР.

Как показано в [10], вероятность h(x) зависит от расстояния 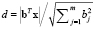от гиперплоскости (3) до точки x до и градиента grad h(x) и вектора-градиента

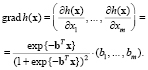
Поскольку в (3) вектор коэффициентов b задан с точностью до произвольного множителя, то введем нормировку: , .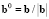

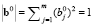Считаем 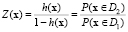, т.е. , .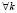

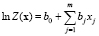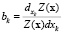Если приравнять 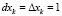, то последняя формула в процентах примет вид: 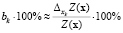. То есть значение bk показывает, на сколько процентов изменится отношение 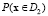к 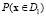при увеличении Xk на единицу при фиксации остальных показателей.

Производная функции Z(x) по Xk прямо пропорциональна коэффициенту bk. Рост (уменьшение) функции Z(x) равносилен увеличению (уменьшению) h(x). Следовательно, для увеличения значения h(x) приращения Δx_k должны быть положительными для bk > 0 и отрицательными, если bk < 0.

По статистическим данным за 2013 г. были сформированы два класса регионов [10]. В класс D1 были включены регионы с уровнем ИЧР не выше 0,84. В класс D2 попали регионы с уровнем ИЧР не менее 0,85. С целью повышения достоверности результатов были удалены из рассмотрения регионы с очень низким и очень высоким уровнем ИЧР и с пропусками в данных. Используемые социально-экономические показатели и рассчитанные коэффициенты уравнения (3) для классификации регионов по ИЧР указаны в табл. 1.

Из табл. 1 видим, что для увеличения вероятности h(x) (повышения качества жизни в регионе) необходимо:

– уменьшать значения показателей X1, X6, X7, X9, X10, X12, X13 (коэффициенты bi отрицательные),

– увеличивать значения показателей X2, X3, X4, X5, X8, X11 (коэффициенты bi положительные).

Отметим, что максимальное значение коэффициента b4 = 10,004 объясняется кейнсианской теорией [11].

Коэффициенты уравнения (2) были определены по данным за 2013 г. (табл. 1). Исследуем адекватность модели на статистических данных за следующий 2014 г. на примере областей Уральского федерального округа. В табл. 2 приведены фактические значения ИЧР и оценки вероятностей h(x) за 2013–2014 гг. Отметим, что в 2013 г. вероятности h(x) находились по обучающим выборкам, а в 2014 г. – по имеющимся тестовым статистическим данным по формуле (2). При расчете количественных значений признаков X4, X5, X12, X13 за 2014 г. денежные показатели пересчитывались с учетом инфляции, оцениваемой через индекс потребительских цен.

Тюменская область имеет в обоих случаях наибольшее значение ИЧР, что соответствует максимальной вероятности h(x), практически равной 1. Росту значений ИЧР в остальных областях соответствует увеличение для всех трех регионов вероятностей h(x).

Результаты исследования и их обсуждение

В [10] был сформулирован подход к управлению регионом в виде оптимизационных задач повышения качества жизни посредством увеличения вероятности h(x) отнесения его к классу регионов с высоким ИЧР. Рассмотрим эти задачи. Первая задача – это максимизация вероятности h(x) при ограничениях на изменения социально-экономических показателей

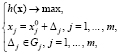(5)

где x⁰ – вектор значений показателей; Gj и Δj – область допустимых значений изменения и изменение компоненты Xj соответственно.

В задаче (5) grad h(x) всегда ортогонален гиперплоскости (2) и не учитываются экономические ограничения и затраты, необходимые для изменения социально-экономических показателей. Поэтому ее решением будет точка пересечения вектора 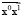(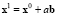, a > 0) с границей допустимой области.

Ниже учтем экономические ограничения и затраты на изменения Xj

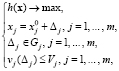(6)

где Vj и vj(Δj) – предельная величина затрат и функция затрат на изменение Xj соответственно.

Таблица 1

Показатели и коэффициенты уравнения (3)

Таблица 2

Фактические значения ИЧР и оценки вероятностей h(x) отнесения субъектов УрФО к группе регионов с высоким качеством жизни за 2013–2014 гг.

Достижение функцией h(x) заданной вероятности p0 при минимальных затратах на изменение вектора x можно представить в виде задачи

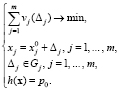(7)

Значение целевой функции в задачах (5)–(7) позволяет оценить прямые последствия реализации заданного воздействия на объект, а косвенные – в каждом конкретном случае можно определить на основе полученного в результате решения оптимизационной задачи значения вектора x.

Отметим, что в задачах (6) и (7) достаточно сложно задавать функции затрат vj(Dj). Обойдем это ограничение, сформулировав задачу следующим образом:

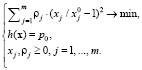(8)

Здесь решается вопрос перехода региона в состояние h(x) = p0 при минимальном среднеквадратическом относительном изменении значений компонент вектора социально-экономических показателей. Такая постановка не требует задавать в явном виде трудоемкость изменения показателей Xj. Весовые коэффициенты rj позволяют учесть особенности, связанные с изменением переменных. Если априорная информация о показателях Xj, включенных в (2), отсутствует, то считаем все rj равными 1.

Нулевое значение весового коэффициента можно использовать в ситуациях, когда знак коэффициента bj имеет противоположное направление по сравнению с желаемым, позволяет зафиксировать фактическое значение показателя Xj. Например, здесь b1 = –2,381 < 0, данная ситуация вызвана имеющейся закономерностью, связанной с тем, что в регионах с более высоким качеством жизни рождаемость ниже по сравнению с регионами с низким качеством жизни. Это в [12] названо обратной связью рождаемости с уровнем жизни. Поскольку вектор b определяется по обучающей выборке и отражает сложившуюся социально-экономическую ситуацию в стране, данный вопрос не может решаться в рамках рассматриваемых оптимизационных задач.

Введя в задачу (8) дополнительные ограничения на предельные изменения компонент, учитывающие особенности изменения социально-экономических показателей Xj, получим

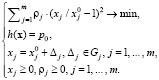(9)

Апробируем логистическую регрессию как модель управления (8) на примере Курганской, Свердловской и Челябинской областей, считая ρj = 1, j = 1, 2, ..., m.

Курганская область относится к регионам с низким уровнем ИЧР. Вероятность отнесения ее к регионам с высоким уровнем ИЧР: h(x0) = 0,005. В табл. 3 представлены результаты управления с целью выхода Курганской области на пороговый уровень (h(x*) = 0,5), полученные с помощью решения задачи (8). Для сопоставления расчетных значений показателей в табл. 3 приведены фактические значения за 2013 г. (год исходных значений для проведения расчетов) и 2016 г., а также целевые значения показателей, взятые из указов Президента РФ № 596-600 и № 606 от 07.05.2012.

Расчетные (оптимальные) значения социально-экономических показателей показывают тот минимальный уровень, достижение которого позволить субъекту РФ повысить значение ИЧР. Поэтому расчетные значения показателей не могут выступать в качестве новых предлагаемых целевых ориентиров, но их следует принимать во внимание при оптимизации затрат и уточнении приоритетов дальнейшего развития.

Для Курганской области приоритетами в повышении качества жизни должны стать: а) увеличение продолжительности жизни населения (X2) до 70 лет (этот уровень в целом по России был достигнут еще в 2012 г., но для данной области при изначально его невысоком значении является оптимальным и реалистичным ориентиром); б) развитие ипотечного жилищного кредитования (X3), объемы которого в последние годы были серьезно сокращены в результате макроэкономической нестабильности; в) рост инвестиционной активности (X4) позволит увеличить производство, а также привлечь свободную рабочую силу и повысить платежеспособность населения; г) снижение уровня безработицы (X10) до 6,7 %.

Свердловская область обладает относительно высоким уровнем ИЧР. Результаты решения оптимизационной задачи, в которую было заложено достижение более высокого уровня ИЧР, соответствующее увеличению вероятности h(x) до 0,95, представлены в табл. 4.

Важным условием увеличения вероятности роста ИЧР в Свердловской области является экономический рост, невозможный без дополнительных инвестиций (X4). Развитие же ипотечного жилищного кредитования (X3) способствует привлечению инвестиций в строительную отрасль – драйвера экономического роста территории.

Таблица 3

Фактические, целевые и расчетные показатели Курганской области

Примечание: * – за 2015 г.; ** – значение рассчитано, исходя из установленного целевого значения количества выдаваемых ипотечных жилищных кредитов в размере 815 тысяч в год в целом по России при сохранении численности населения на уровне 2012 г.

Челябинская область отнесена к регионам со средним уровнем ИЧР с вероятностью h(x0) = 0,805. При решении оптимизационной задачи повышения ИЧР были заложены три варианта увеличения h(x). Результаты решения для трех вероятностей h(x1) = 0,85, h(x2) = 0,9, h(x3) = 0,95 приведены в табл. 5.

Можно рассматривать разные варианты развития Челябинской области в зависимости от возможностей региона. Чем благоприятнее наблюдаемая динамика по показателям, тем выше вероятность повышения качества жизни в области. Однако по отдельным показателям (X2, X5, X10, X12 и X13) разница в их значениях по трем сценариям незначительна или отсутствует, что говорит об оптимальности данных значений для анализируемой региональной системы. В Челябинской области приоритетом в повышении качества жизни населения должно стать ипотечное кредитование (X3).

Выводы

1. Показано, что бинарную логистическую регрессии можно использовать как математическую модель в задачах мониторинга и управления многомерными системами.

2. Бинарная логистическая регрессия как модель управления апробирована на примере задачи повышения качества жизни регионов.

Работа выполнена при поддержке РФФИ, грант № 20-41-660008 р_а.

Библиографическая ссылка