Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Асхакова Ф.Х. 1

---

1 ФГБОУ ВО «Карачаево-Черкесский государственный университет имени У.Д. Алиева»

В работе описаны результаты исследования прибыльности двойственной балансовой модели, позволяющей учитывать экологические требования. Здесь ставилась цель разработать методику неотрицательного решения рассматриваемой модели и на основании этой разработки реализовать программный продукт и использовать полученные результаты для анализа прибыльности модели ЗАО «Карачаевский пивзавод». Для реализации этой цели в работе описываются критерии прибыльности модели. В разработанной методике неотрицательного решения модели применяются следующие методы: матричный метод, если рассматриваемая модель является хорошо обусловленной; метод регуляризации для случая, когда рассматриваемая модель является плохо обусловленной. Здесь обусловленность модели определяется числом обусловленности матрицы. Приводится подробное описание алгоритма реализации разработанной методики, которая была реализована в программу с помощью языка программирования. Статистические данные ЗАО «Карачаевский пивзавод» за 2017–2019 годы применены для разработки таблицы его межотраслевого баланса, из которой была построена балансовая модель. С помощью разработанной программы производится исследование прибыльности в разработанной двойственной модели ЗАО «Карачаевский пивзавод», которая позволяет учитывать экологические требования. Проведенные исследования показывают, что исследуемая модель является прибыльной. Приводятся выводы результата исследования.

Статья в формате PDF

0 KB

модель

двойственная к модели Леонтьева-Форда

Карачаевский пивзавод

метод регуляризации

матричный метод

прибыльность

1. Стаховский В.А., Зенкин А.А., Павлова М.Н., Капц И.В. Модели, описанные моделью Леонтьева-Форда // Наука и современность: материалы Региональной научно-практической конференции. Политехнический институт (филиал) ДГТУ в г. Таганроге. 2018. С. 96–98.

2. Торопцев Е.Л., Мараховский А.С. Эквивалентирование динамического межотраслевого баланса при решении задач устойчивости // Вестник Российского фонда фундаментальных исследований. Гуманитарные и общественные науки. 2019. № 2 (95). С. 65–76.

3. Хрущ Л.З., Коржевская Е.П. Расширение межотраслевой эколого-экономической модели Леонтьева-Форда // Бизнес информ. 2012. № 3. С. 75–78.

4. Асхакова Ф.Х., Лайпанова З.М. Решение модели, двойственной к модели Леонтьева – Форда, методом регуляризации (по Тихонову) // Гуманитарные и социально-экономические науки. 2016. № 1. С. 120–124.

5. Никайдо Х. Выпуклые структуры и математическая экономика. М.: Мир, 1972. 518 с.

6. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. Учебное пособие для вузов. Изд. 3-е, испр. М.: Наука. Главная редакция физико-математической литературы, 1986. 288 с.

7. Сумин М.И. Метод регуляризации А.Н. Тихонова для решения операторных уравнений первого рода: учебно-методическое пособие. Нижний Новгород: Нижегородский госуниверситет, 2016. 56 с.

8. Асхакова Ф.Х. Решение плохо обусловленной модели, двойственной к модели Леонтьева-Форда, учитывающей утилизацию вредных отходов // Вестник Астраханского государственного технического университета. Серия: Управление, вычислительная техника и информатика. Астрахань: Изд-во АГТУ, 2016. № 3. С. 87–93.

На сегодняшний день актуальным является не только эффективное применение производственных ресурсов в целях получения оптимальной прибыли, но и ликвидация производственных отходов, чтобы поддерживать соответствующий уровень экологического состояния.

Некоторые производственные отходы подлежат повторной переработке. При производстве появляются производственные отходы, некоторые из них целесообразнее переработать, после чего появляются повторные вредоносные отходы. Появляется проблема утилизации повторных вредоносных отходов, а значить дополнительных расходов для этой цели. Как в первом, так и во втором случае для переработки и ликвидации производственных отходов предприятиям приходится тратить некоторое количество средств.

Важно отметить, что для решения данной проблемы в некоторых случаях применяют балансовые модели. На сегодняшний день исследованию балансовых моделей посвящены многие работы, например [1–3].

Исходя из этого, представляет интерес исследование модели, двойственной к модели Леонтьева-Форда.

Цель исследования: исследование модели, двойственной к модели Леонтьева-Форда, разработка методики ее неотрицательного решения и программная реализация этой методики. Применение полученных результатов для анализа модели ЗАО «Карачаевский пивзавод».

Материалы и методы исследования

Материалами исследования являются статистические данные за 2017–2019 годы ЗАО «Карачаевский пивзавод», модель, двойственная к модели Леонтьева-Форда. Для решения рассматриваемой модели в работе используются матричный метод и метод регуляризации.

Результаты исследования и их обсуждение

Рассмотрим балансовую модель вида:

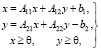(1)

где 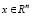– вектор валового выпуска;

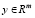– вектор вредных отходов;

b1 – вектор конечного спроса, размера n;

b2 – вектор остаточного уровня вредоносных отходов, размера m;

A11 – матрица размера n×n;

A12 – матрица размера n×m;

A21 – матрица размера m×n;

A22 – матрица размера m×m.

Модель (1) называют обобщенной моделью Леонтьева-Форда.

Запишем (1) в виде:

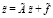, (2)

где ;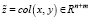

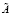– четырех блочная матрица размера :

;

.

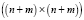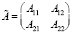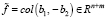Существует модель, двойственная к модели (1) вида [4, c. 120–121]:

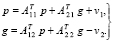(3)

,

где 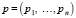– вектор цен;

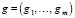– вектор расходов утилизации вредоносных отходов;

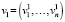– вектор, характеризующий добавленную стоимость;

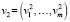– вектор величины убытка от неликвидированных отходов;

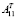(n×n) – матрица, транспонированная к матрице A11 из (1);

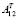(n×m) – матрица, транспонированная к матрице A12 из (1);

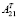(m×n) – матрица, транспонированная к матрице A21 из (1);

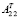(m×m) – матрица, транспонированная к матрице A22 из (1).

Перепишем (3) в виде:

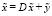, (4)

или

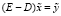, (5)

где ;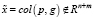

D – матрица:

;

.

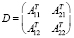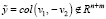Известно, что модель (2) является продуктивной, если она имеет неотрицательное решение 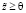при некоторых положительных ;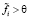

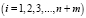- модель (2) является разрешимой в 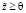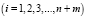при ;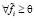

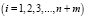- блочная матрица 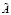с элементами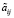 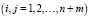должна иметь n + m положительных последовательных главных миноров;

- все главные миноры блочной матрицы 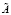положительны.

Решение модели (2) устойчиво, если блочная матрица A является хорошо обусловленной .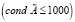

По аналогии модель (4) считается прибыльной, если она обладает неотрицательным решением 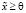при некоторых положительных ;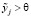

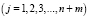- модель (4) является разрешимой в 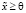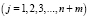при ;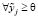

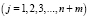- блочная матрица D с элементами 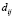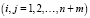, должна иметь n + m положительных последовательных главных миноров;

- все главные миноры блочной матрицы D должны быть положительными.

Решение модели (4) считается устойчивым, если .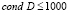

Продуктивность в (2) при некотором наборе положительных величин 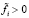влечет за собой не только продуктивность в (2) при любом наборе неотрицательных 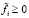, но и прибыльность в (4) при любом наборе неотрицательных 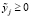. Возможность безубыточного назначения цен в (4) при некотором наборе положительных 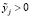не только гарантирует такую возможность при любом наборе неотрицательных 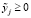, но и означает продуктивность в (2) при любом наборе неотрицательных величин .

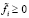Рассмотрим критерии продуктивности и прибыльности, т.е. условия Брауэра-Солоу.

Пусть

,

,

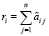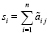где ri – строчная сумма коэффициентов блочной матрицы 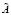, sj – столбцовая сумма коэффициентов блочной матрицы .

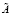Следствие (условия Брауэра-Солоу) [5, с. 127]. Каждое из следующих двух условий является достаточным для продуктивности в (2) и одновременно для прибыльности (4): ; .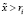

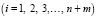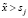
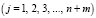Обозначим 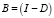, тогда (5) примет вид:

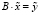. (6)

Для решения задачи (6) будем применять два метода. Если 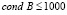, то задачу будем решать матричным методом:

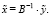(7)

В противном случае будем применять регуляционный метод [6, с. 114–129].

Пусть вместо точных значений матрицы B и вектора 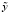имеем их приближенные значения B* и 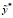, тогда модель (6) примет следующий вид:

.

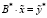Обозначим через ζ – абсолютную погрешность B*, а через δ обозначим абсолютную погрешность 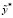и допустим, что

,

.

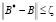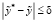Из [7, с. 41] следует, что поиск решения (6) сводится к нахождению 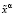, который минимизирует сглаживающий функционал:

,

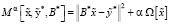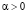, (8)

где 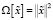– стабилизирующий функционал, α = α(δ) – параметр регуляризации. При этом, как это показано в [4; 6], существует один вектор 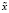, который может быть определен при всяком фиксированном α > 0 из системы

,

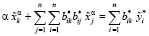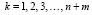. (9)

Рассмотрим для поставленной задачи алгоритм его решения:

1. Вводим n, m.

2. Вводим A11, A12, A21, A22.

3. Вводим v1, v2.

4. Создаем блочный вектор .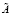

5. Создаем блочную матрицу D, трансформированную к блочной матрице .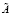

6. Вычисляем .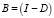

7. Проверяем выполнимость следующего условия .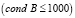

8. Если условие из пункта 7 выполняется, то вычисляем (7), иначе переходим к пункту 9.

9. Задаем α1 > 0.

10. При заданном значении α1, находим 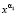системы (9).

11. При известных значениях α1, 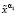вычисляем значение 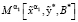функционала (8).

12. Задаем α2 > 0, α2 < α1.

13. При заданном значении α2 находим 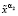системы (9).

14. При известных значениях α2, 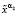вычисляем значение 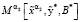функционала (8).

15. Если

,

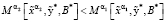то переходим к пункту 17.

16. Если

,

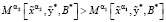то присваиваем .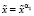

17. Задаем α3 > 0, α3 < α2.

18. При заданном значении α3 находим 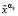системы (9).

19. При известных значениях α3, 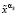вычисляем 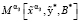функционала (8).

20. Если

,

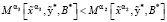то переходим к пункту 22.

21. Если

,

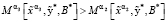то присваиваем .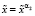

22. Задаем α4 > 0, α4 < α3.

И так далее, этот процесс продолжаем до тех пор, пока на (k + 1)-м шаге не отыщем 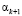, , 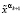при которых

.

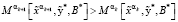В данном случае считаем 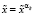и вычисления останавливаем.

Таблица межотраслевого баланса (тыс. руб.)

С помощью языка программирования Delphi 7 произведена программная реализация описанного алгоритма.

Используем статистические данные ЗАО «Карачаевский пивзавод» 2017–2019 гг. для построения таблицы межотраслевого баланса (тыс. руб.) (таблица).

На основе таблицы построим следующие матрицы:

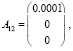
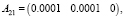
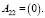
Пусть предприятию необходимо увеличить свою прибыль на 15 % по сравнению с предыдущими годами, тогда вектор добавленной стоимости будет равен:

,

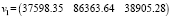а вектор, который характеризует размер убытка от отходов, не подлежащих утилизации – v2 = (0).

Введя в программу значения n, m, A11, A12, A21, A22, v1, v2, получим следующий результат:

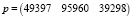, g = (5.13).

Результаты исследования показали, что для увеличения прибыли на 15 % относительно предыдущих лет в 2021 г. ЗАО «Карачаевский пивзавод» должен будет произвести продукцию первого цеха на сумму 49 397 тыс. руб., второго цеха на сумму 95 960 тыс. руб., третьего цеха на сумму 39 298 тыс. руб., а на ликвидацию производственных отходов необходимо будет потратить 5.13 тыс. руб.

Заключение

Из результатов работы видно, что двойственная модель ЗАО «Карачаевский пивзавод» является прибыльной, а это значит, что балансовая модель предприятия является продуктивной.

Разработанная методика может быть использована для нахождения неотрицательного решения двойственной балансовой модели, а разработанная в ходе исследовании программа может быть применена для анализа прибыльности балансовой моделей предприятия с учетом экологического состояния.

Данная работа обобщает и дополняет результат работы [4; 8].

Библиографическая ссылка