Безработица на современном этапе развития выступает в качестве одной из важнейших социальных проблем для стран с рыночной и развивающейся экономикой. Показатели безработицы характеризуют состояние экономики в стране в целом.
Анализ и прогнозирование динамики безработицы во всех странах, в том числе в РФ, является актуальной задачей при разработке перспективных решений в области экономики. Получению адекватных моделей и надёжных прогнозов препятствует наличие в статистической информации аномальных наблюдений, вызванных различными обстоятельствами [1–3].
С начала кризиса в 2008 г. уровень безработицы в России растет. По официальным данным темпы роста безработицы в 2009 г. снизились, а летом рост безработицы и вовсе прекратился. Однако уровень безработицы сохранился, несмотря на принятые меры по созданию рабочих мест, а также на летний сезон, который всегда характеризуется усилением активности в строительной отрасли и промышленности.
В марте 2019 г., по данным Росстата, как безработные классифицировались 3,5 млн россиян, или 4,7 % рабочей силы [4].
Наиболее высокие значения показатель «Количество безработных (в среднем за период) (UNEMPL_Q)» принимает в первых трех кварталах 2009 г. и в первом квартале 2010 г. Проанализируем, являются ли эти наблюдения аномальными.
Цель исследования: выявление аномальных наблюдений при анализе динамики безработицы в Российской Федерации с 2007 по 2019 г. с использованием процедуры декомпозиции временного ряда на сезонную, трендовую составляющие и на остатки, использующей метод локальных регрессий, реализованный в пакете anomalize программной среды R [5–7].
В исследовании использованы данные по безработице в России за период с первого квартала 2007 г. по четвертый квартал 2019 г. [8].
Проанализируем наличие аномальных наблюдений в данных и рассмотрим основные возможности пакета anomalize программной среды R для обнаружения необычных наблюдений во временных рядах.
Процесс обнаружения аномальных наблюдений пакетом anomalize можно разделить на три части:
- Декомпозиция временных рядов с помощью функции time_decompose().
- Обнаружение аномалий в остатках с помощью функции anomalize().
- Преобразование нижней и верхней границ аномалий с помощью функции time_recompose().
1. Разложение временных рядов – функция time_decompose().
Функция time_decompose() осуществляет разложение временного ряда – разделение его на составляющие компоненты: тренд, сезонная компонента и остаток. Она вызывается на первом шаге процесса обнаружения аномальных наблюдений. Возможно использование одного из двух методов разложения временных рядов: STL или Twitter. Метод STL осуществляет декомпозицию временных рядов с помощью метода локальных регрессий (LOESS) и скользящей средней. В методе Twitter используются устойчивые (робастные) оценки весовых коэффициентов взвешенной регрессии при вычислении сезонных коэффициентов. Важными параметрами функции являются frequency – частота – контролирует количество сезонных компонент. Для квартальных данных оно равно 4 и trend – тенденция – управляет шириной окна в методе локальных регрессий на последнем шаге, при сглаживании ряда, состоящего из тренда и остаточной компоненты.
По умолчанию для декомпозиции используется метод stl (Seasonal-Trend Decomposition Procedure Based on Loess). Это процедура декомпозиции временного ряда на сезонную, трендовую составляющие и на остатки, использующая метод локальных регрессий (LOESS).
Метод локальных регрессий (LOESS)
Метод локальной регрессии предназначен для сглаживания временных рядов. Он был разработан для анализа зависимостей между значениями переменных, когда эти зависимости имеют сложный вид и не могут быть описаны в терминах традиционной линейной и нелинейной регрессии. В этом случае область значений независимой переменной X можно покрыть конечным числом отрезков, для каждого из которых далее находят свою регрессию традиционным методом – как правило, линейную или квадратичную. Количество таких регрессий выбирают равным числу наблюдений. Для каждого наблюдения (x, y) строится своё уравнение взвешенной регрессии по ближайшим точкам, yj = α0 + α1xj +… αmxjm + ε. Степень многочлена m выбирается не более 2. Вектор оценок коэффициентов регрессии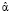 
определяется из условия минимизации взвешенной суммы квадратов остатков регрессии. Вычисленные по уравнениям регрессии значения 
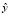представляют собой сглаженный ряд значений y.
В расчётах для оценки коэффициентов регрессии участвуют только q ближайших точек, (q ≤ n), расстояние которых от точки x не превосходит величины r, xi∈(x – r, x + r). Число q задаётся либо непосредственно пользователем, либо через заданную пользователем долю участвующих в регрессии наблюдений β, и тогда q равно целой части произведения n•β. Веса наблюдений хi выбираются с помощью весовой функции W(z) таким образом, чтобы вес ближайших к x точек был наибольшим и уменьшался бы с удалением от точки х, для которой строится уравнение регрессии. Функция W(z) должна удовлетворять следующим условиям:
1) W(z) > 0, если |z| < 1;
2) W(z) = 0, если |z| ≥ 1;
3) W(–z) = W(z);
4) W(z) не возрастающая функция z.
В качестве аргумента функции W(z) выступает расстояние от xi до x, масштаб которого выбран таким образом, чтобы для всех xi, участвующих в регрессии, модуль z был меньше 1, а для всех остальных – больше или равен 1;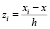 
, где h – расстояние от x до наиболее удалённой от x среди участвующих в регрессии точек. Поскольку W(–z) = W(z), то в качестве z можно брать как положительное, так и отрицательное значение расстояния от xj до x, то есть разность xi – x можно брать при вычислении z без модуля. Вес точки xj, попавшей в окно для xi, равен 
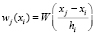. В качестве весовой используются биквадратная и трикубическая функции:
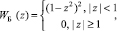
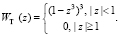
Вектор оценок коэффициентов взвешенной регрессии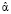 
определяется из условия минимизации взвешенной суммы квадратов остатков регрессии
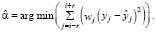
Биквадратная функция имеет более гладкое распределение весов, чем трикубическая функция; значения, располагающиеся ближе к центру, по биквадратной функции имеют меньшие веса, чем по трикубической. Стоит также заметить, что сумма весов взвешенной регрессии не равна 1, но это для построения LOESS и не требуется, поскольку при вычислении коэффициентов локальных регрессий важны не веса, а соотношения между их величинами.
Алгоритм разложения временного ряда на три составляющие
Метод STL является широко используемой процедурой для декомпозиции временных рядов с аддитивными составляющими, когда временной ряд является суммой тренда, сезонной составляющей и ошибок [9].
Сезонная компонента вычисляется итерационно. На первом шаге алгоритма удаляем тренд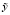 
, в результате получаем для всех i сумму сезонной компоненты и остатка: 
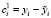(верхний индекс 1 указывает на шаг внутри цикла, на котором получена компонента 
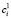). В начале процесса разложения ряда, когда 
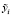неизвестны, можно положить 
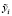равными нулю и тогда получим 
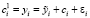. Однако на последующих шагах компоненты будут разделены и начальное приближение не отразится на оценках компонент.
На втором шаге алгоритма разделения ряда на составляющие каждая сезонная компонента сортируется по периодам, после чего сглаживается с помощью LOESS. В нашем случае сглаживаются все значения первого квартала, затем второго и так далее. Параметр LOESS q – ширину окна – рекомендуется выбирать не менее 7, чтобы реакция LOESS на случайные отклонения была не очень сильной. После выполнения второго шага получаем ряд сезонных компонент для каждого периода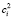 
. Число точек T в каждом периоде равно n/s, где s – число периодов; в нашем случае s = 4, n = 52, T = 13.
При сглаживании сезонной компоненты для каждого сезона вычисляем дополнительно s точек слева и справа от периода, то есть вычисляются сглаженные значения не для T, а для T + 2s точек. Эти точки потребуются для следующих шагов.
На третьем шаге алгоритма полученные сезонные компоненты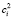 
сглаживаются по периодам дважды с помощью скользящей средней порядка s, а затем – скользящей средней третьего порядка. В результате убираются дополнительные 2s точек из каждого периода, вычисленные на предыдущем шаге. После этого ряд ещё раз сглаживается с помощью LOESS с q = r(low), равным наименьшему нечётному числу, большему s. В нашем примере q = 5. После выполнения третьего шага получаем третий ряд значений сезонной компоненты 
.
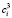На четвёртом шаге, с целью избежать попадания трендовых компонент в сезонные коэффициенты, рассчитываются окончательные сезонные коэффициенты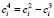 
.
На пятом шаге из исходного ряда данных вычитаются сезонные коэффициенты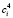 
. В результате получаем сумму трендовой составляющей и остатка: 
.
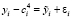На шестом шаге получаем оценку тренда, сглаживая полученный ряд с помощью LOESS с параметром q = rtrend. Величина rtrend выбирается в пределах от 1,5s до 2s. Это позволяет избавиться от остатков сезонных составляющих в ряде остатков.
В итоге мы получили все значения тренда, сезонные коэффициенты и остатки. Последовательность шагов 1–6 можно повторить ещё k раз, однако опыт показывает, что в этом нет необходимости [10].
В результате выполнения функции time_decompose() выдаются четыре столбца:
- observed – наблюдаемые, фактические значения;
- season – сезонный или циклический тренд. По умолчанию используется еженедельная сезонность;
- trend – долгосрочный тренд. Значение по умолчанию составляет 3 месяца;
- remainder –остаток, который используется для анализа выбросов, получаемый как разница между фактическими значениями и значениями тренда и сезонности.
Фрагмент протокола (первые 10 наблюдений) работы функции time_decompose() приведен на рис. 1. На рис. 2 результат работы функции time_decompose() представлен в виде графика.
2. Обнаружение аномалий в остатках с помощью функции anomalize().
После выполнения декомпозиции временных рядов и получения остатков с желаемыми характеристиками остатки могут быть проанализированы на наличие аномальных наблюдений. Ряд остатков получается после удаления из исходных данных обеих систематических компонент. Наблюдения, выходящие за рамки ожидаемых и сильно отличающиеся от остальных, оказывают сильное воздействие на оценки регрессионного уравнения и могут привести к неверным выводам на основе этих уравнений. Обнаружение аномалий выполняется на остатках, полученных после удаления из временных рядов обеих систематических компонент.
Функция anomalize реализует два теста: IQR – интерквартильный размах («interquartile range») и GESD – «Generalized Extreme Studentized Deviate».
Тест IQR. Если ряд остатков имеет нормальное распределение, то значения ряда, отклоняющиеся от среднего более чем на 3σ (σ – среднеквадратическое отклонение), можно считать аномальными. Однако не всегда есть основания, чтобы отнести распределение ошибок к нормальному. Для выборок с отличным от нормального распределением целесообразно использовать метод интерквартильного интервала (IQR). IQR вычисляется как разница между 75- и 25-перцентилями и графически отображается в виде «ящика с усами». М-перцентиль QM – это число, меньше которого находится М % от выборки. 50-процентиль – это середина выборки (медиана) или среднее от двух величин посередине. IQR равен разности между 75-процентилем и 25-процентилем, IQR = Q75 – Q25. Аномальными признаются наблюдения, расположенные ниже нижней границы или выше верхней границы. В качестве нижней границы выбирается число Q25 – 1,5•IQR, в качестве верхней – Q75 + 1,5•IQR. Чтобы определить слишком экстремальные выбросы, вместо величины 1,5•IQR берут 3•IQR. Иногда вместо 1,5•IQR берут для нижней границы Q25 – Q5, а для верхней границы – Q95 – Q75.
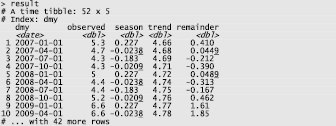
Рис. 1. Результат работы функции time_decompose()
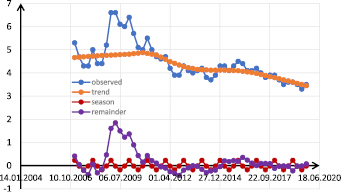
Рис. 2. График исходных данных и результатов выполнения функции time_decompose(). Выполнен в Excel
Тест GESD. Метод GESD (Generalized Extreme Studentized Deviate Test) постепенно устраняет выбросы, используя t-критерий Стьюдента, сравнивая статистику теста с критическим значением. Каждый раз, когда выброс удаляется, тестовая статистика обновляется. Как только тестовая статистика падает ниже критического значения, все выбросы считаются удаленными. Поскольку этот метод предполагает непрерывное обновление, он медленнее, чем метод IQR. Тем не менее это, как правило, самый эффективный метод для удаления выбросов.
Метод GESD используется в AnomalyDection: Anomalydetections().
Тест GESD [11] используется для обнаружения одного или нескольких выбросов в одномерном наборе данных, имеющих примерно нормальное распределение. Тест GESD требует указания верхней границы r для предполагаемого количества выбросов в ряде остатков ei. Тест, по существу, выполняет последовательно r отдельных тестов: тест на один выброс, тест на два выброса и так далее вплоть до r выбросов. Он проверяет нулевую гипотезу H0 = {в данных нет выбросов} против конкурирующих Hi = {в данных есть i выбросов}, i = 1,…, r. Тестовая статистика имеет вид
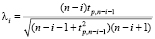, i = 1,…,r,
где t_(p,ν) – 100p-процентная точка t-распределения с ν степенями свободы и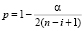 
, α – уровень значимости. Номер выброса определяется как наибольшее i из таких, что Ri > λi. Исследования, проведенные Роснером [11], показали, что получаемые таким путём значения являются очень точными для n ≥ 25 и достаточно точными для n ≥ 15. Хотя обобщенный ESD по существу является тестом Граббса, применяемым последовательно, но проведённые расчёты показали, что в некоторых случаях с помощью последовательного применения теста Граббса выявляется меньше влиятельных точек, чем с помощью ESD.
Обнаружение аномалий
Результатом работы функции anomalize() являются три новых столбца – remainder_l1 и remainder_l2 (нижняя и верхняя границы, за пределами которых наблюдения считаются аномалиями), а также индикаторная переменная anomaly, которая принимает значение «No», если наблюдение не является выбросом, и «Yes» если да. На рис. 3 и 4 приведены результаты работы функции anomalize().
3. Преобразование нижней и верхней границ аномалий с помощью функции time_recompose().
Функция time_recompose() восстанавливает исходный временной ряд с использованием значений из season, trend, remainder_l1 и remainder_l2 и попутно рассчитывает два новых столбца – recomposed_l1 и recomposed_l2, которые соответствуют верхней и нижней границам диапазона «нормальных» наблюдений. После того, как анализ временных рядов завершен, создаются три новых столбца.
– remainder_l1: нижний предел остатка;
– remainder_l2: верхний предел остатка;
– аномалия: колонка сообщает, является ли наблюдение аномалией или нет.
На рис. 5 приведен график исходных данных и результатов выполнения функции time_recompose(). Аномальные наблюдения находятся вне доверительного интервала. Они обозначены красными точками. Аномальные наблюдения соответствуют значениям показателя «Количество безработных (в среднем за период) (UNEMPL_Q)» в первых трех кварталах 2009 г. и в первом квартале 2010 г.
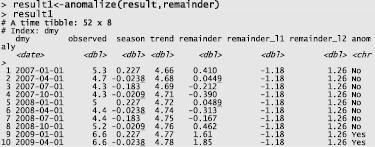
Рис. 3. Результат работы функции anomalize(). Фрагмент протокола (первые 10 наблюдений)
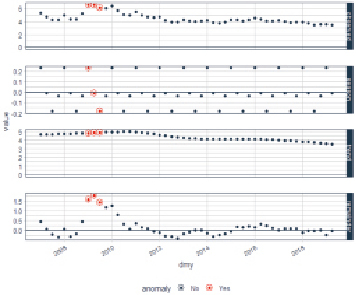
Рис. 4. График результатов выполнения функции anomalies(). Приведены 4 графика: исходные данные, сезонная компонента, тренд и остатки. Красными точками выделены аномальные наблюдения. Выполнен в R
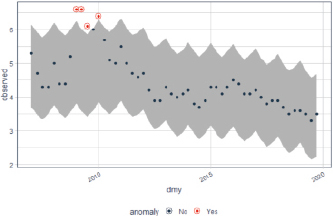
Рис. 5. График исходных данных и результатов выполнения функции time_ recompose(). Выполнен в R
Заключение
Анализ динамики безработицы в РФ показал, что мировой кризис 2008 г. сказался на уровне безработицы в РФ в первом квартале 2009 г., во втором квартале он остался на аномально высоком уровне, в третьем квартале он, как и следовало ожидать, снизился, но всё ещё остался на аномально высоком уровне, далее он немного снизился и вошёл в доверительные границы, но близко к верхней границе, а затем вновь подрос и вышел за доверительные границы и только затем начал постепенно входить в ожидаемые границы. Графики аномальных наблюдений, приведённые выше, наглядно демонстрируют происходящие в данных изменения и помогают при анализе и прогнозировании показателей, представленных временными рядами.
Библиографическая ссылка
Орлова И.В. ВЫЯВЛЕНИЕ АНОМАЛЬНЫХ НАБЛЮДЕНИЙ ПРИ АНАЛИЗЕ ДИНАМИКИ БЕЗРАБОТИЦЫ В РОССИЙСКОЙ ФЕДЕРАЦИИ // Фундаментальные исследования. – 2020. – № 5. – С. 142-148;URL: https://fundamental-research.ru/ru/article/view?id=42761 (дата обращения: 23.11.2024).