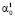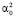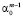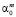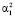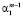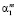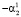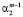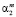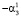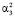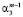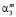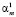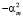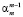Построение эконометрических моделей, их анализ и прогнозирование эндогенной переменной Y по значениям экзогенных переменных X1, X2, …, Xm, зачастую затруднено наличием мультиколлинеарности исходных переменных. Переменные называют мультиколлинеарными, если они связаны корреляционной связью почти линейно [1]. В практических исследованиях экзогенные переменные, как правило, в той или иной степени коррелированы. Методы обнаружения мультиколлинеарности реализованы практически во всех пакетах программ эконометрического моделирования [2–4]. Нежелательные последствия мультиколлинеарности приводят к необходимости тем или иным способом избавиться от нее или ослабить степень мультиколлинеарности [5]. Самым распространённым приёмом ослабления мультиколлинеарности является удаление из модели «виновных в мультиколлинеарности» исходных переменных. Однако это приводит к обеднению модели, к невозможности исследовать достаточно полно влияние экзогенных переменных на эндогенную переменную. Другой приём состоит в линейном преобразовании переменных, приводящем к новым, ортогональным, переменным. Обычно речь идёт о преобразовании к главным компонентам. Однако главные компоненты, являясь линейными комбинациями всех экзогенных переменных, плохо поддаются содержательной интерпретации и потому значения коэффициентов регрессии по главным компонентам мало что говорят исследователю о влиянии исходных переменных на Y. К тому же последние главные компоненты, соответствующие близким к нулю и фактически незначимым собственным числам ковариационной матрицы исходных переменных, неустойчивы к незначительным колебаниям исходных переменных и их обычно удаляют из модели. Третьим способом борьбы с мультиколлинеарностью является применение ридж-регрессии для оценки коэффициентов регрессии. Однако при этом оценки получаются смещёнными, и пользоваться этим методом надо с осторожностью.
В данной работе предлагается метод неполной ортогонализации исходных переменных путём замены переменных, приводящий к поддающимся содержательной интерпретации результатам и позволяющий, в силу взаимно-однозначного соответствия исходных и новых переменных, получать прогнозные оценки значения Y, переходить при необходимости от коэффициентов регрессии по новым переменным к коэффициентам регрессии по исходным регрессорам. При этом получены соответствующие формулы перехода для коэффициентов регрессии, ковариационных матриц коэффициентов регрессии, вычисления прогнозных значений новых переменных по прогнозным значениям исходных переменных.
Материалы и методы исследования
Суть предлагаемого метода состоит в том, что некоторые переменные, коррелированные с другими, заменяются на остатки от регрессии этих переменных на другие регрессоры, имеющие с ними корреляционную связь. При этом никаких допущений относительно этих остатков не делается. Полученные коэффициенты уравнений регрессии используются только для вычисления остатков, которые равны разности между самой заменяемой переменной и вычисленными по уравнению регрессии значениями этой переменной. Таким образом, новые переменные являются линейными комбинациями исходных переменных и константы. Предлагаемый метод замены переменных позволяет существенно уменьшить степень мультиколлинеарности.
Результаты исследования и их обсуждение
Рассмотрим линейную регрессию эндогенной переменной Y на экзогенные переменные X1, X2…., Xm. Количество наблюдений равно n. Сведём наблюдения значений независимых переменных Xj в матрицу X размерности n×(m + 1), первый столбец матрицы X состоит из единиц.
Спецификация модели линейной регрессии имеет вид
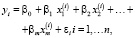 (1)
(1)
где 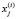 – значение Xj в i-м наблюдении, εi – остаточный член регрессии, удовлетворяющий условиям Гаусса – Маркова.
– значение Xj в i-м наблюдении, εi – остаточный член регрессии, удовлетворяющий условиям Гаусса – Маркова.
Допустим, что регрессоры мультиколлинеарны и среди них есть группы тесно связанных между собой переменных. Выберем последовательно в каждой группе одну или несколько переменных и с помощью метода наименьших квадратов (МНК) определим коэффициенты дополнительных регрессий выбранных переменных на остальные переменные группы. Остатки этих регрессий обозначим через Uj. Далее будем называть выбранные регрессоры Xj, которые выступали в роли зависимых переменных в дополнительных регрессиях, «выбранными» переменными, а остальные регрессоры Xj – «не выбранными» переменными.
Уравнение регрессии «выбранных» Xj на «не выбранные» регрессоры группы имеет вид
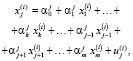 (2)
(2)
где 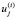 – остатки Uj от регрессии Xj на остальные регрессоры в i-м наблюдении,
– остатки Uj от регрессии Xj на остальные регрессоры в i-м наблюдении, 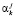 – коэффициент регрессии Xj при переменной Xk. Коэффициенты регрессии в (2), как отмечалось, будем находить с помощью МНК, при этом никаких допущений относительно остатков Uj не делается.
– коэффициент регрессии Xj при переменной Xk. Коэффициенты регрессии в (2), как отмечалось, будем находить с помощью МНК, при этом никаких допущений относительно остатков Uj не делается.
Из (2) получаем
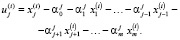 (3)
(3)
Как видим, Uj являются линейной комбинацией исходных регрессоров X1, X2…., Xm и константы.
Обозначим через U матрицу значений новых регрессоров размерности n×(m + 1). По столбцам матрицы, соответствующим «выбранным» Xj, находятся 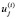 – значения остатков Uj для наблюдения i, столбцы, соответствующие «не выбранным» Xj, равны соответствующим столбцам матрицы X; элементы первого столбца
– значения остатков Uj для наблюдения i, столбцы, соответствующие «не выбранным» Xj, равны соответствующим столбцам матрицы X; элементы первого столбца 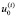 равны единице.
равны единице.
Рассмотрим матрицу A преобразования переменных Xj, представленного формулой (3). Для «выбранных» Xj элементы матрицы определяются равенством (3), для «не выбранных» Xj столбцы матрицы A равны единичному вектору с единицей на (j + 1)-ом месте, поскольку Uj = Xj. Матрица преобразования переменных A, если бы все Xj заменялись бы на остатки регрессий Xj на все остальные регрессоры, имела бы вид
|
1 |
– |
|
. . . |
– |
– |
|
|
0 |
1 |
– |
. . . |
– |
– |
|
|
A = |
0 |
|
1 |
. . . |
– |
– |
|
0 |
|
– |
. . . |
– |
– |
|
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
|
0 |
– |
|
. . . |
– |
1 |
В соответствии с (3) матрицы X и U удовлетворяют равенству
U = X·A. (4)
Остатки Uj коррелируют между собой гораздо меньше, чем Xj между собой. Поэтому, если исходные переменные Xj даже мультиколлинеарны, Uj могут быть почти ортогональны и потому вычисление коэффициентов регрессии и их интерпретация по новым переменным не связано с преодолением мультиколлинеарности регрессоров.
Матрица A является невырожденной (если только Xj не являются строго мультиколлинеарными). Отсюда получаем, что преобразование переменных, определяемое матрицей A, является взаимно-однозначным.
Обозначим через γ и β векторы коэффициентов регрессии Y на новые переменные и на Xj соответственно, 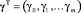 ,
, 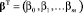 . Поскольку преобразование, определяемое матрицей A, является взаимно-однозначным, то минимумы суммы квадратов остатков обеих регрессий, т.е. Y-X·β и Y-U·γ, совпадают и вектор остатков регрессии Y на новые переменные совпадает с вектором остатков от регрессии Y на Xj. Очевидно, совпадают и коэффициенты детерминации обеих регрессий.
. Поскольку преобразование, определяемое матрицей A, является взаимно-однозначным, то минимумы суммы квадратов остатков обеих регрессий, т.е. Y-X·β и Y-U·γ, совпадают и вектор остатков регрессии Y на новые переменные совпадает с вектором остатков от регрессии Y на Xj. Очевидно, совпадают и коэффициенты детерминации обеих регрессий.
Получим формулу, описывающую взаимосвязь γ и β.
Уравнения регрессий Y на Uj и Xj можно записать в виде
Y = X·β + ε, (5)
Y = U·γ + ε. (6)
Подставим (4) в (6):
Y = X•A•γ + ε. (7)
Сравнивая (7) с (5), получаем формулу, показывающую взаимосвязь коэффициентов регрессии:
β = A·γ. (8)
Ковариационную матрицу cov(β) вектора коэффициентов регрессии β вычисляем исходя из того, что коэффициенты регрессии βj являются, в соответствии с (8), линейными комбинациями коэффициентов γk (k = 0,1,…,m),
cov(β) = A·cov(γ)·AT.
Коэффициенты γj регрессии Y на новые переменные можно трактовать как приращение Y при изменении Xj на единицу, учитывающее соответствующие изменения остальных регрессоров, то есть при условии, что корреляционная матрица регрессоров при этом не изменяется. В этом случае мы трактуем каждую выбранную переменную как состоящую из двух частей. Одна часть формируется под влиянием корреляционных связей с другими регрессорами, а другая часть – Uj представляет собой «специфическую компоненту», не связанную или слабо связанную с остальными регрессорами Xj. Если меняем на единицу только сам этот фактор, не затрагивая его корреляционных связей с другими факторами, то меняем только его «специфическую» часть, а это и есть остаток Uj.
Для прогнозирования значения Y при значениях регрессоров, равных Xпр = (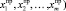 , можно воспользоваться уравнением регрессии по исходным переменным (5). Однако можно и не переходить к регрессии по Xj, а воспользоваться уравнением регрессии по Uj. Для этого надо вычислить прогнозное значение Uпр =
, можно воспользоваться уравнением регрессии по исходным переменным (5). Однако можно и не переходить к регрессии по Xj, а воспользоваться уравнением регрессии по Uj. Для этого надо вычислить прогнозное значение Uпр = 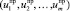 по формуле (4): Uпр = Xпр•A и далее воспользоваться оценками коэффициентов уравнения регрессии (6).
по формуле (4): Uпр = Xпр•A и далее воспользоваться оценками коэффициентов уравнения регрессии (6).
Предложенный метод уменьшения мультиколлинеарности проиллюстрируем на примере данных, описанных в работе [3, с. 130], так как данная статья является логическим ее продолжением.
Наличие межфакторных связей проверим с помощью матрицы коэффициентов парной корреляции. На рис. 1 представлена визуализация корреляционной матрицы, полученная в среде R.
На рис. 2 приведены результаты построения регрессии Y на X1, X2, X3, X4, X5 в среде R. Коэффициент детерминации достаточно высокий – 0,89; уравнение регрессии значимо, а все его коэффициенты незначимы (р = 0,01), что является признаком частичной (нестрогой) мультиколлинеарности.
Тестирование мультиколлинеарности с помощью наиболее популярного метода факторов инфляции дисперсии (VIF) в среде R [6] не только подтвердило наличие мультиколлинеарности (VIF>5), но и выявило факторы, приводящие к ней – Х1 и Х5 (рис. 3).
> library("PerformanceAnalytics")
> tabgr <- tab11[, c(1,2,3,4,5)]
> chart.Correlation(tabgr, histogram=TRUE)
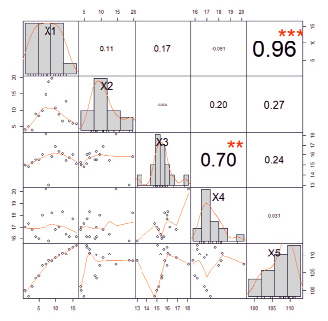
Рис. 1. Матрица коэффициентов парной корреляции
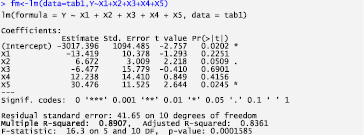
Рис. 2. Результат оценки параметров регрессионной модели по всем факторам
Результат выполнения функции eigprop [7–8] (тестирование мультиколлинеарности по методу Белсли) [9–10] приведен на рис. 4. Наибольшее значение индекса обусловленности (CI) в строке 6, равное 376,49, свидетельствует о наличии мультиколлинеарности. В этой строке наибольшие значения среди факторов имеют Х1 и Х5, значит, между этими факторами существует тесная взаимосвязь (заметим, что, по сравнению с предыдущими тестами, появилась новая информация – в пятой строке зафиксирована тесная взаимосвязь между переменными Х3 и Х4). В таких случаях рекомендуется одну из переменных, Х1 или Х5, удалить из модели. В данном случае целесообразно удалить Х1, тем более что и Р-значение t-статистики коэффициента регрессии при Х1 равно 0,225, и знак коэффициента регрессии отрицательный, в то время как коэффициент корреляции между Y и X1 положительный.
Однако мы не станем удалять Х1, а заменим Х5 на сумму слагаемых X5 = 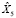 + U5, где
+ U5, где 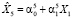 . Оценивать коэффициенты
. Оценивать коэффициенты 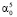 и
и 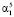 будем с помощью МНК. Уравнение регрессии примет вид
будем с помощью МНК. Уравнение регрессии примет вид
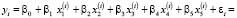
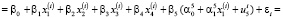
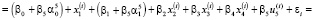
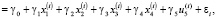 (9)
(9)
где 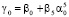 ,
, 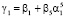 ,
, 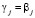 , j = 2, 3, 4, 5; εi – остаточный член регрессии.
, j = 2, 3, 4, 5; εi – остаточный член регрессии.
Оценим параметры модели 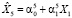 (рис. 5) и получим остатки U5 = X5 –
(рис. 5) и получим остатки U5 = X5 – 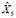 .
.

Рис. 3. Факторы инфляции дисперсии параметров регрессии Y по всем переменным
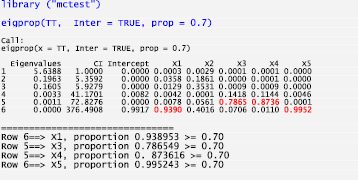
Рис. 4. Результат диагностики коллинеарности по методу Белсли [3, с. 133]

Рис. 5. Результат оценки параметров регрессионной модели «выбранного» фактора X5
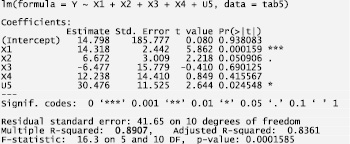
Рис. 6. Результат оценки параметров регрессионной модели по новым переменным
Далее оценим параметры модели 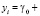
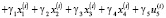 (рис. 6).
(рис. 6).
Коэффициент регрессии β5 при U5 оказался тем же самым, что и коэффициент регрессии при X5. Коэффициент регрессии β1 при X1 отличается от нового коэффициента регрессии при X1 на величину 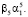 Связь между коэффициентами регрессии βj и γj можно получить и без выкладок (9) – по формуле (8): β = A·γ, где матрица A преобразования (3) в данном случае имеет вид
Связь между коэффициентами регрессии βj и γj можно получить и без выкладок (9) – по формуле (8): β = A·γ, где матрица A преобразования (3) в данном случае имеет вид

У нас
βT = (-3017,4; -13,42; 6,67; -6,48; 12,24; 30,48)
γT = (14,80; 14,32; 6,67; -6,48; 12,24; 30,48)
Подставляя в (8) A и γ, получаем приведённый выше вектор β. Итак, получили, что уравнение регрессии на новые переменные имеет вид
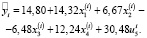
В это уравнении регрессии значимо вошли X1, X2, U5 (рис. 6). Коэффициент детерминации равен 0,89.
Далее можно было бы попытаться решить проблему мультиколлинеарности, связанную с Х3, Х4. Однако эти переменные слабо коррелируют с Y и их включение в модель мало изменит коэффициент детерминации. К тому же на основании больших P-значений у нас есть все основания исключить Х3, Х4 из модели регрессии. Окончательно получаем модель с тремя переменными Х1, Х2, U5 (рис. 7). Все P-значения коэффициентов не превосходят 0,02. Коэффициент детерминации уменьшился менее чем на 0,01.
Все VIF(j) не превосходят 1,64 (рис. 8). Как видим, после выполненных преобразований мультиколлинеарность в данных практически отсутствует.
Сравним коэффициенты регрессии и их характеристики уравнений регрессии Y по X1, X2, U5 и Y по X1, X2, X5 (табл. 1) и (табл. 2).
Таблица 1
Параметры результирующей модели регрессии
|
γ0 |
γ1 |
γ2 |
γ5 |
|
|
const |
X1 |
X2 |
U5 |
|
|
Коэффициент |
121,9 |
13,85 |
7,23 |
30,95 |
|
t-статистика |
4,01 |
6,40 |
2,72 |
3,01 |
|
P-значение |
0,00 |
<0,0001 |
0,02 |
0,01 |
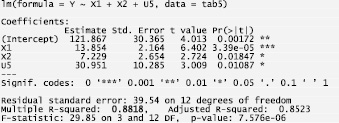
Рис. 7. Результат оценки параметров регрессионной модели по переменным Х1, Х2, U5

Рис. 8. Факторы инфляции дисперсии параметров регрессии Y по переменным Х1, Х2, U5
Таблица 2
Параметры модели регрессии по исходным переменным X1, X2, X5
|
β0 |
β1 |
β2 |
β5 |
|
|
const |
X1 |
X2 |
X5 |
|
|
Коэффициент |
2958 |
–14,32 |
7,23 |
30,95 |
|
t-статистика |
2,93 |
–1,52 |
2,72 |
3,01 |
|
P-значение |
0,01 |
0,15 |
0,02 |
0,01 |
Коэффициенты β2 и β5 и их характеристики совпадают с γ2 и γ5, а β1 не только не близок к γ1, но имеет отрицательный знак, несмотря на положительный коэффициент корреляции Y с X1. Очевидно, что по коэффициентам β уравнения регрессии Y по исходным переменным нецелесообразно анализировать степень влияния отдельных регрессоров на Y. В то же время, после замены переменных, если бы регрессоры были бы ортогональны, коэффициенты регрессии нормированного уравнения регрессии были бы равны коэффициентам корреляции регрессоров с Y. У нас же регрессоры не строго ортогональны и коэффициенты корреляции Y с X1 не строго, а приблизительно равны соответствующим коэффициентам регрессии. Коэффициент корреляции Y с X1 равен 0,678, а коэффициент нормированного уравнения регрессии при X1 равен 0,641. Это подтверждает высказанное выше утверждение относительно интерпретации коэффициентов регрессии по новым переменным, полученным после замены переменных.
Заключение
Предложенный метод неполной ортогонализации исходных переменных путём замены переменных позволяет уменьшить степень мультиколлинеарности регрессоров, получить интерпретируемые коэффициенты уравнения регрессии и оценить вклад каждого фактора в изменение эндогенной переменной.
Библиографическая ссылка
Орлова И.В. ПОДХОД К РЕШЕНИЮ ПРОБЛЕМЫ МУЛЬТИКОЛЛИНЕАРНОСТИ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ // Фундаментальные исследования. 2019. № 5. С. 78-84;URL: https://fundamental-research.ru/ru/article/view?id=42464 (дата обращения: 10.03.2026).