Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Адамадзиев К.Р. 1

---

1 ФГБОУВО «Дагестанский государственный университет»

Целью исследования является построение уравнений рядов динамики, характеризующих тенденции зависимостей между показателями суммарных затрат, материальных затрат и затрат на оплату труда животноводства региона от соответствующих затрат растениеводства по данным за семь лет и оценка их характеристик. Для достижения цели решен ряд задач: сформировано исходное информационное обеспечение; методами традиционной экономики и новыми методами моделирования выявлены тенденции в динамике затрат сельского хозяйства и проведен прогноз; разработан алгоритм и рассчитаны параметры и статистические характеристики уравнений рядов динамики; созданы таблицы с результатами и проведен их анализ. Проведена оценка тенденций традиционными методами экономики на основе темпов роста затрат в сельском хозяйстве в целом, в двух его отраслях по годам к 2016 г., а также на основе структуры затрат по годам. Методами математического и компьютерного моделирования проверены зависимости показателей суммарных затрат, материальных затрат и затрат на оплату труда в сельском хозяйстве Республики Дагестан в целом, в растениеводстве и животноводстве. В качестве исходной информации выступают статистические данные затрат сельского хозяйства за 2010–2016 гг. Для выявления динамических тенденций построены и проверены на приемлемость по пять видов уравнений временных рядов и рядов динамики: линейный, степенной, показательный, гиперболический, параболический. Рассчитаны параметры и статические характеристики проверяемых уравнений и проведен их сравнительный анализ. Разработана методика прогнозирования каждого показателя затрат в сельском хозяйстве на основе уравнений временных рядов и рядов динамики, выражающих зависимости одних видов затрат от других. Предложены несколько вариантов возможных объемов затрат в растениеводстве и животноводстве РД на трехлетний прогнозный период (2017–2019 гг.). Определены минимальные и максимальные величины темпов роста затрат в двух рассматриваемых отраслях сельского хозяйства Республики Дагестан, а также их возможные минимальные и максимальные удельные веса в 2019 г.

Статья в формате PDF

0 KB

регион

сельское хозяйство

растениеводство

животноводство

затраты

тенденции

моделирование

уравнение

ряды динамики

стохастика

связь

зависимость

анализ

метод

1. Программа «Цифровая экономика Российской Федерации» [Электронный ресурс]. URL: http://government.ru/ rugovclassifier/614/events (дата обращения: 24.10.2018).

2. Семь определений цифровой экономики [Электронный ресурс]. URL: https://www.crn.ru/news/detail.php?ID=116780 (дата обращения: 24.10.2018).

3. Кундиус В.А. Экономика агропромышленного комплекса: учеб. пособие. М.: КНОРУС, 2010. 544 с.

4. Эконометрика: учебник / Под ред. И.И. Елисеевой. 2-e изд., перераб. и доп. М.: Финансы и статистика, 2005. 576 с.

5. Адамадзиев К.Р. Отношения, зависимости и динамические тенденции показателей России, ЮФО и Республики Дагестан: статистико-эконометрическая оценка // Сегодня и завтра российской экономики. Научно-аналитический сборник. Спец. выпуск. 2009. С. 30–40.

Термин «Цифровая экономика» стал в настоящее время одним из популярных [1]. Например, в статье [2] приводятся семь определений, сформулированных на уровне правительств и организаций международного уровня, из которых наиболее удачными нам представляются: (а) Всемирного банка, который под цифровой экономикой понимает «Систему экономических, социальных и культурных отношений, основанных на использовании цифровых информационно-коммуникационных технологий; (б) Исследовательского центра журнала «Economist» и компании IBM – которые цифровой называют «Экономику, способную предоставить высококачественную ИКТ-инфраструктуру и мобилизовать возможности ИКТ на благо потребителей, бизнеса и государства». Ключевыми словами в этих определениях являются цифровые технологии и интернет.

Цель исследования: методами цифровизации выявить и оценить зависимости показателей затрат животноводства региона (всех, материальных и на оплату труда) от соответствующих затрат растениеводства по данным Республики Дагестан за семь лет (2010–2016 гг.). Для достижения цели решен ряд задач: традиционными методами и методами моделирования выявлены тенденции в динамике затрат сельского хозяйства; разработан алгоритм и рассчитаны параметры и характеристики уравнений рядов динамики; разработана авторская методика прогнозирования показателей затрат в сельском хозяйстве на основе моделей рядов динамики; созданы аналитические таблицы, проведен их анализ и сформулированы выводы.

Материалы и методы исследования

В качестве объекта исследования выбраны показатели затрат отраслей сельского хозяйства Республики Дагестан за 2010–2016 гг. При выявлении тенденций применены различные методы и разработаны математические и компьютерные модели

Результаты исследования и их обсуждение

Сельское хозяйство представлено двумя взаимосвязанными сферами: растениеводством (зерновым хозяйством, овощеводством, садоводством, виноградарством и др.) и животноводством (крупным и мелким рогатым скотом, птицеводством, пчеловодством, рыбным хозяйством и др.). В экономике, в том числе сельского хозяйства, следует различать понятия связи и зависимости. Связь – более широкое понятие, означающее, что большинство показателей корреляционно взаимосвязаны в силу их стохастичности, зависимость – более узкое и строгое понятие, означающее, что одни показатели корреляционно не просто связаны с другими, но и зависят от них по экономической логике. Например, стоимость какой-либо продукции растениеводства не зависит, а корреляционно связана с площадью сельских угодий и численностью занятых работников, в то же время объем продукции растениеводства не просто корреляционно связан, а зависит от урожайности сельхозкультур.

Говоря о связях и зависимостях в экономике, в том числе в экономике сельского хозяйства, следует различать следующие ситуации:

а) если один из показателей корреляционно связан с другим, то этот другой показатель также может быть корреляционно связан с первым, то есть два показателя взаимосвязаны;

б) если один из показателей зависит от другого показателя, то этот другой может быть как зависимым от первого, так и независимым (но обязательно связанным).

Экономические показатели растениеводства и животноводства корреляционно взаимосвязаны. Но при этом часть показателей животноводства корреляционно зависит от показателей растениеводства. Это объясняется тем, что растениеводство создает кормовую базу для животноводства [3].

В настоящем исследовании нами выявлены, описаны показатели затрат животноводства от показателей затрат растениеводства и проведен анализ их корреляционной зависимости.

В качестве исходных данных использованы величины показателей суммарных затрат (Yt), материальных затрат (MZt) и затрат на оплату труда (ZPt) в сельском хозяйстве РД, в растениеводстве и животноводстве по данным за 2010–2016 гг. На наличие корреляционной зависимости нами проверены зависимости Y1t от Y2t, MZ1t от MZ2t, ZP1t от ZP2t, где показатели с цифрой «единица» являются показателями затрат животноводства, а с цифрой «два» – показателями затрат растениеводства. Рассматриваемые зависимости являются парными. Наличие или отсутствие зависимости в первую очередь целесообразно проверить графически. Построенные нами графики и их анализ показывает, что показатели затрат в животноводстве предположительно зависят от соответствующих показателей растениеводства и эти зависимости имеют линейный или весьма близкий к нему криволинейный характер. Поскольку заранее нельзя однозначно определить вид зависимости, на приемлемость нами проверено пять видов уравнений рядов динамики: линейный, показательный, степенной, гиперболический и параболический.

Для описания и оценки вида зависимости принято рассчитывать и анализировать параметры и статические характеристики уравнений, выражающих динамические тенденции [4]. В табл. 1 приведены величины параметров и ряда статистических характеристик для четырех видов построенных нами уравнений.

Анализ наличия и приемлемости связей (зависимостей) принято начинать с индекса детерминации (r2), принимающего значения от 0 до 1 (нулевое значение означает отсутствие корреляции, единица – означает, что зависимость является функциональной, а не корреляционной). По величинам индекса детерминации (r2) все виды уравнений, выражающие тенденции показателей затрат на оплату труда, оказались неприемлемыми. Поэтому нет необходимости в их анализе. По индексу детерминации (r2) и критерию Фишера приемлемыми оказались уравнения линейного (1-е место), параболического (2-е место) и степенного (3-е место) видов, выражающих тенденции.

В соответствии с величинами индекса детерминации (r2) все четыре уравнения приемлемы для описания зависимости всех затрат в животноводстве от затрат в растениеводстве. По приемлемости их можно расположить в следующей последовательности: параболический – линейный – степенной – показательный (гиперболический вид оказался неприемлемым); по величинам индекса детерминации (r2), выражающим степень зависимости материальных затрат в животноводстве от материальных затрат в растениеводстве, все уравнения оказались приемлемыми; по приемлемости эти уравнения можно расположить в следующем порядке: параболический – линейный – гиперболический – степенной – показательный. Затраты на оплату труда в животноводстве оказались некоррелированными от соответствующих затрат в растениеводстве, то есть ни один из пяти видов уравнений не оказался приемлемым.

По экономическому смыслу параметров из табл. 1 (б) при прочих равных условиях уравнения по предпочтительности можно расположить в следующем порядке: линейное – степенное – параболическое – показательное.

Отличительной особенностью уравнений линейного и степенного видов, делающей их наиболее приемлемыми, является возможность экономического истолкования их параметра (m) при показателе-факторе:

а) в соответствии с уравнением линейного вида, если независимый показатель-фактор увеличится на одну единицу, то результативный или зависимый показатель возрастет на m единиц;

б) в соответствии с уравнением степенного вида, если показатель-фактор увеличится на 1 %, то зависимый (результативный) показатель возрастет на m %.

Таблица 1

Величины параметров и характеристик уравнений, выражающих тенденции в динамике зависимости показателей затрат в животноводстве от затрат в растениеводстве по данным Республики Дагестан за 2010–2016 гг.

а) статистические характеристики

б) параметры уравнений тенденций

Построенные нами уравнения линейного и степенного вида, выражающие зависимость всех затрат (Y1t) и материальных затрат (MZ1t) животноводства от соответствующих затрат (Y2t, MZ2t) растениеводства, приведены ниже:

а) линейные

Y1t = –5544999 + 1,1759*Y2t;

MZ1t = –46431 + 1,1890*MZ2t;

б) степенные

Y1t = 0,0055*;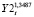

MZ1t = 0,1827*.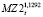

Степень корреляционной зависимости затрат на оплату труда в животноводстве от соответствующих затрат в растениеводстве оказалась низкой и неприемлемой; поэтому такую корреляцию нет необходимости исследовать. В соответствии с величинами m в уравнениях линейного вида, если увеличить все затраты и материальные затраты в растениеводстве на 1 руб., то все затраты и материальные затраты в животноводстве возрастут на 1,175 и 1,189 руб. соответственно. В соответствии с величинами m в уравнениях степенного вида, если все затраты и материальные затраты в растениеводстве увеличить на 1 %, то эти виды затрат в животноводстве возрастут на 1,35 и 1,13 %.

Особое положение занимают уравнения параболического вида, при построении которых определяются два параметра при показателях-факторах (m1, m2) [5]:

Y = b + m1X + m2X2.

Важная отличительная особенность уравнений параболического вида состоит в том, что с их помощью можно определить максимальные (или минимальные) величины зависимого показателя (Y), а также величины показателя-фактора (X), при которой достигается этот максимум (минимум). Для вышеприведенного уравнения параболы величина X, при которой величина Y будет max (или min) определяется по формуле Xo = – 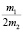. При этом, если m2 больше 0, то величина Y будет наименьшей, если m2 меньше 0, то величина Y будет наибольшей; если существует Ymax, то Ymin не существует, и наоборот.

Ниже приведена математическая запись уравнений параболического вида, выражающая тенденции в динамике зависимостей показателей затрат в животноводстве (Y1t, MZ1t) от соответствующих затрат в растениеводстве (Y2t, MZ2t):

а) для всех затрат

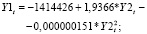
б) для материальных затрат

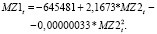
Параболический вид уравнения позволяет определить точку максимума (или минимума); в нашем случае нет ни максимума, ни минимума, то есть приемлемой оказалась одна ветвь параболы. Но максимальные (или минимальные) величины двух рассматриваемых показателей затрат в сельском хозяйстве РД по этим уравнениям можно рассчитать. В нашем случае эти величины оказались максимумами.

Одной из важных целей выявления тенденций в динамике экономических показателей является прогнозирование [4]. Однако при разработке прогнозов в экономике нет необходимости каждый раз выявлять, описывать и анализировать тенденции в виде трендовых или иных моделей. Прикладные программные средства и компьютерные технологии позволяют разрабатывать прогнозы с помощью специальных встроенных функций. Эти функции как бы в уме строят такие модели и их алгоритмы и автоматически выполняют все расчеты и процедуры обработки информации.

Так, в «мастере функций...» MS Excel имеется ряд встроенных статистических функций, позволяющих разрабатывать варианты прогнозов экономических показателей по исходным данным, организованным в виде Excel-таблиц:

а) линейного вида – «предсказ» или «тенденция»;

б) показательного вида – «рост».

Для выполнения прогнозных расчётов по моделям степенного, гиперболического и параболического видов могут быть использованы встроенные функции «тенденция» или «предсказ».

Прогнозировать можно каждый экономический показатель в отдельности, а также зависимый показатель на основе независимого показателя-фактора [3]. Математический инструмент при этом будет иметь следующую схематическую запись: а) Yit = fi(t); б) Yit = f(Xit), где Yit, Xjt – величины i-го зависимого и j-го независимого показателей в t-м временном периоде, t = 1,2,...,T – последовательность временных периодов.

Главной целью прогнозных расчётов является, с нашей точки зрения, не разработка единственно желательного варианта с точки зрения того или иного руководителя экономического объекта (такие варианты прогнозов не могут существовать в принципе), а предсказание верхних, нижних пределов прогнозных величин показателей, а также двух-трех наиболее реально возможных вариантов прогнозов. Сказанного можно достичь, только применив системный подход, основой которого является математическое и компьютерное моделирование. В частности, выполнив в ходе проведения настоящего исследования множество расчётов, автор предлагает четыре варианта затрат в растениеводстве и животноводстве РД на трехлетний прогнозный период (2017–2019 гг.).

В табл. 2 приведены абсолютные величины затрат в двух рассматриваемых отраслях и в целом в сельском хозяйстве, а также темпы роста этих затрат по годам к 2016 г.

Учитывая важность структуры затрат для анализа, в табл. 3 приведены также удельные веса растениеводства и животноводства в суммарных затратах сельского хозяйства.

Таблица 2

Абсолютные величины и темпы роста затрат в сельском хозяйстве РД, рассчитанные по вариантам прогнозов с помощью уравнений динамических тенденций за 2010–2016 гг.

Таблица 3

Удельные веса растениеводства и животноводства РД в прогнозных величинах показателей затрат, рассчитанных по уравнениям динамических тенденций за 2010–2016 гг.

Согласно четырём вариантам прогнозов из табл. 2 и 3, удельный вес растениеводства в 2017–2019 гг. может снизиться на 28 % (с 50 до 43–48 %) при таком же росте удельного веса животноводства, т.е. от 50 до 53–57 %.

Отметим, что проведенное исследование является актуальным, а разработанные методы и модели отличаются научной новизной.

На основании выполненного исследования можно сделать следующие выводы:

– среди экономических показателей сельского хозяйства особо значимыми являются показатели затрат; добываются их относительно более низкого роста при увеличении результативных показателей (объемов производства, урожайности, продуктивности скота и др.) является одной из важных задач экономических объектов, связанных с развитием сельского хозяйства;

– решению этой задачи может способствовать, с нашей точки зрения, выявление и оценка связей, зависимостей и тенденций показателей затрат как между собой, так и с другими показателями сельскохозяйственных объектов;

– выявление и оценку тенденций показателей затрат, а также разработку прогнозов затрат можно проводить по предложенной автором в настоящем исследовании методике, основывающейся на системном подходе с применением различных методов классической экономики и модельно-компьютерных инструментариев.

Библиографическая ссылка