Мембранная технология считается передовой в химическом производстве. Мембранные методы широко применяются для разделения и очистки жидких смесей, изменения их концентрации. В химической промышленности мембранные методы используются в составе простых и многостадийных технологических процессах [1]. Наиболее важными преимуществами мембранной технологии являются: переработка промышленных сред без фазовых превращений, простота конструкций мембранных аппаратов, высокая экономичность, низкая энергоемкость и др. Однако мембранным методам свойственно явление концентрационной поляризации, которое заключается в повышении концентрации задерживаемых веществ у поверхности мембраны [2]. Вследствие этого происходит снижение производительности мембраны. Для уменьшения негативного влияния концентрационной поляризации, как правило, турбулизируют прилегающий к поверхности мембраны слой жидкости использованием различного рода турбулизаторов.
Цель исследования: разработка математической модели изменения гидродинамических условий в мембранном аппарате, в составе которого имеется турбулизирующий элемент. Моделирование гидродинамических условий позволит установить эффективность использования турбулизирующего элемента, установить рациональные значения его основных конструктивных параметров и рассчитать потери мощности на элементе.
Материалы и методы исследования
Объектом моделирования являются гидродинамические условия в мембранном аппарате с турбулизирующим элементом в виде перфорированной конической вставки [3]. Мембранный аппарат состоит из цилиндрического корпуса, с одной стороны которого имеется штуцер для подачи исходной среды, с другой стороны расположен штуцер для отвода конечного продукта (сконцентрированной среды). На внешней стенке корпуса установлен штуцер для отвода очищенного продукта. В корпусе аппарата коаксиально установлена полупроницаемая трубчатая мембрана. В канале мембраны расположен турбулизирующий элемент в виде конической вставки, боковая поверхность которой перфорирована. Предполагается, что направленный поток среды, выходя из отверстий турбулизирующего элемента, увеличивает степень турбулизации среды внутри мембраны, что обеспечивает снижение толщины слоя задерживаемых веществ на ее поверхности и повышает производительность мембранного аппарата.
Выявим основные закономерности, происходящие при движении перерабатываемой среды по длине турбулизирующего элемента. Предположим, что мембранной переработке подвергается слабоконцентрированная жидкая среда. Основными характеристиками, подлежащими определению, в таком случае являются: расход и скорость течения среды, а также потери давления по длине турбулизирующего элемента. Выделим фрагмент элемента (рис. 1).
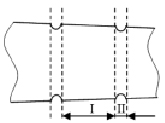
Рис. 1. Фрагмент турбулизирующего элемента
Движение жидкой среды внутри рассматриваемого гидродинамического элемента сопровождается следующими потерями давления: во-первых, потери за счет конического сужения элемента (потери при движении в конфузоре) в зоне I, во-вторых, потери давления при истечении из отверстий, расположенных на боковой поверхности элемента (зона II) [4, 5]. Общей зависимостью, определяющей потери давления на гидродинамическом элементе, является формула [4]:
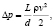 (1)
(1)
где △p – потери давления, Па;
λ – коэффициент гидравлического трения;
L – длина турбулизирующего элемента, м;
d – диаметр турбулизирующего элемента, м;
v – скорость течения жидкости, м/с;
g – ускорение свободного падения;
ρ – плотность жидкой среды, кг/м3.
Потери давления на трение в зоне I определяются формулой [6, 7]:
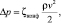 (2)
(2)
где ζконф – коэффициент сопротивления конфузора.
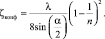 (3)
(3)
Таким образом потери давления на трение при движении жидкой среды в конфузоре:
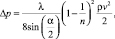 (4)
(4)
где n – степень сужения конфузора.
Коэффициент гидравлического трения l определяется режимом течения жидкости, т.е. числом Рейнольдса (Re). Как правило, течение жидкой среды в трубе, имеющей круглое сечение, характеризуется ламинарным режимом при Re ≤ 2300 [8, 9]. При этом коэффициент гидравлического трения равен
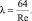 (5)
(5)
Турбулентный режим возникает при значениях
4000 < Re < 10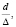
где d – диаметр турбулизирующего элемента, м;
D – шероховатость его поверхности, м.
В этом случае коэффициент гидравлического трения определится как
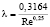 (6)
(6)
или, иначе,
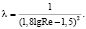 (7)
(7)
Давление среды на выходе зоны I определится разностью давления на ее входе и соответствующих потерь на трение по ее длине:
p2 = p1 – Δp. (8)
В зоне II потери давления обусловлены истечением жидкости из затопленного отверстия, находящегося на боковой поверхности турбулизирующего элемента. Чтобы определить данные потери, необходима скорость истечения среды из отверстия. Она может быть рассчитана, исходя из формулы [10]:
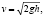 (9)
(9)
где g – ускорение свободного падения;
φ – поправочный коэффициент (принят φ = 0,95);
h – уровень жидкой среды, м.
В этом случае давление определяется формулой
p = φgh. (10)
Тогда
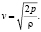 (11)
(11)
Определить потери давления на отверстии позволяет формула (2). Для цилиндрических отверстий коэффициент местного сопротивления составляет ζ = 0,71 [7, 11]. Определение потерь давления в соответствии с формулами (2–11) необходимо повторить по всей длине турбулизирующего элемента.
Скорость течения жидкой среды, необходимая в расчетах потерь давлений, определяется уравнением неразрывности потока в зависимости от исходной (заданной) скорости:
v1S1 = v2S2 = const, (12)
где v1 и S1 – средняя скорость и площадь сечения на входе зоны элемента;
v2 и S2 – средняя скорость и площадь сечения на выходе зоны элемента.
Результаты исследования и их обсуждение
С учетом приведенных формул разработан алгоритм расчета гидродинамических условий по длине турбулизирующего элемента, который позволяет выполнить моделирование течения слабоконцентрированной жидкой среды. К входным данным отнесены геометрические параметры турбулизирующего элемента (рис. 2) – его начальный (d0) и конечный (dn+1) диаметры и длина (L), также расстояние между отверстиями (l) или их количество (n), давление на входе в мембранный аппарат (p), исходная скорость жидкой среды (v), ее плотность и вязкость (ρ и μ).
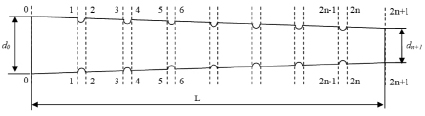
Рис. 2. Внешний вид турбулизирующего элемента
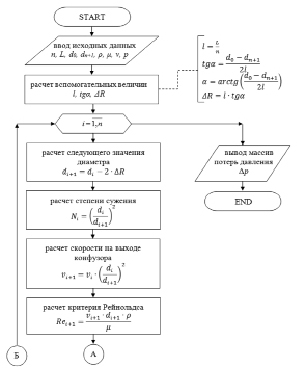
Рис. 3. Блок-схема алгоритма расчета гидродинамических условий по длине турбулизирующего элемента (начало рисунка)
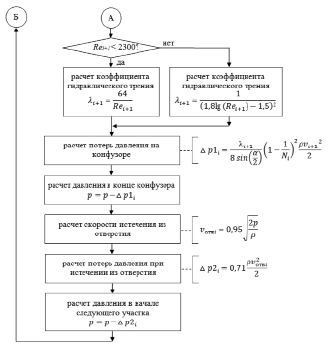
Рис. 3. Блок-схема алгоритма расчета гидродинамических условий по длине турбулизирующего элемента (окончание рисунка)
Блок-схема алгоритма представлена на рис. 3. Программная реализация алгоритма выполнена в среде MatLAB. Авторами получено свидетельство о государственной регистрации программы для ЭВМ [12].
Результатом моделирования является массив скоростей течения жидкой среды и потерь давления по длине турбулизирующего элемента.
Заключение
Предложенная математическая модель изменения гидродинамических условий, в частности скорости движения среды и потерь давления, при течении жидкости по длине турбулизирующего конического перфорированного элемента в зависимости от количества отверстий на его боковой поверхности позволяет осуществить расчет и обоснованный выбор рациональных значений геометрических параметров элемента. Модель предполагает использование при расчетах процессов мембранной переработки слабоконцентрированных жидких сред в зависимости от их плотности и вязкости. Расчет потерь давления на турбулизирующем элементе может быть положен в основу расчета мощности насосного оборудования в составе мембранной установки. Алгоритм расчета является универсальным, его программная реализация позволяет установить рациональные значения конструктивных параметров опытно-промышленного оборудования на основе разработанного мембранного аппарата при переработке различных жидких сред.
Библиографическая ссылка
Котляров Р.В., Шевцова Т.Г., Стефанкин А.Е., Романова В.В., Ивина О.А., Кроль А.Н. МОДЕЛИРОВАНИЕ ГИДРОДИНАМИЧЕСКИХ УСЛОВИЙ ПО ДЛИНЕ ТУРБУЛИЗИРУЮЩЕГО ЭЛЕМЕНТА В СОСТАВЕ МЕМБРАННОГО АППАРАТА // Фундаментальные исследования. 2018. № 12-1. С. 20-24;URL: https://fundamental-research.ru/ru/article/view?id=42345 (дата обращения: 07.03.2026).



