Развитие финансовых рынков определяется, в частности, успешным функционированием фондов прямых инвестиций (ФПИ), предоставляющих финансовые ресурсы предприятиям и способствующих приращению их реальной стоимости. В портфель ФПИ входят компании, акции которых не торгуются на фондовой бирже [1, 2]. Согласно стратегии развития малого и среднего предпринимательства Российской Федерации до 2030 г., одной из основных задач развития финансовых институтов является создание фондов, средства которых направляются на развитие компаний. Интерес к рынку прямых инвестиций сопровождается необходимостью разработки подходов и методов для получения наиболее реалистичной оценки стоимости портфелей проектов ФПИ. В целом роль стратегического планирования деятельности любых организаций финансового сектора экономики в условиях финансового кризиса неуклонно растет и стимулирует исследования в данной сфере.
Основные подходы изложены в работах Г. Марковица [3] и Дж. Тобина [4], предложивших первые прикладные модели оптимального инвестиционного портфеля, основанные на выборе независимых друг от друга пакетов акций с учетом установленных критериев риск/доходность и отличающиеся отсутствием (Г. Марковиц) или наличием (Дж. Тобин) в инвестиционном портфеле безрискового актива (государственных облигаций, облигаций высоконадежных эмитентов, недвижимости и пр.). Значительная доля появившихся позже моделей и методов анализа оптимальных инвестиционных портфелей посвящены совершенствованию и модификации моделей Г. Марковица и Дж. Тобина, с точки зрения учета различных особенностей функционирования финансовых активов на финансовых рынках.
В данной работе предлагается математическая модель ФПИ в форме многопараметрической задачи линейного программирования (МЗЛП), учитывающая такое существенное условие формирования ФПИ, как включение в инвестиционный портфель проектов исключительно производственного содержания. Отметим, что использование МЗЛП позволяет рассматривать ФПИ, количество проектов в которых сопоставимо с реально существующими фондами, и использовать для ее анализа авторский автоматизированный финансово-аналитический программный комплекс [5].
Рассмотрим следующую содержательную постановку задачи оценки эффективности функционирования ФПИ. Допустим, что в портфель фонда включаются проекты по производству продукции (n) видов (отраслей, видов экономической деятельности и др.). Указанные проекты характеризуются различным уровнем своей эффективности, которая, в частности, может определяться средней рентабельностью, средней фондоотдачей основных производственных фондов и/или другими показателями. Проекты характеризуются различным уровнем и количеством (K) рисков функционирования. Предположим, что проекты в портфеле ФПИ могут быть проинвестированы в разные моменты времени. Моменты открытия и закрытия проектов произвольны и могут не совпадать с моментами закрытия всего фонда. Предполагается, что проекты ФПИ могут реализовываться в течение длительного срока (3–15 лет), что предусмотрено российским законодательством. Также учитывается вознаграждение менеджерам управляющей компании за управление активами. Размер комиссии закрепляется в договоре доверительного управления [6, 7]. Необходимо определить оптимальные объемы инвестиций в каждый проект ФПИ в соответствии с критерием максимизации дисконтированного сальдо потоков доходов и расходов по сумме всех проектов портфеля ФПИ, с учетом рисков его функционирования.
Рассмотрим следующий механизм страхования рисков создания и функционирования ФПИ (например, волатильность рынков, колебания курсов валют, политические, страновые, экологические и пр.) путем рассмотрения дополнительной группы искомых переменных. Определим риск кризисного функционирования ФПИ как «…потери вследствие неправильно поставленной или недостигнутой стратегической цели» [8]. Для численной оценки риска, на наш взгляд, целесообразно использовать такой показатель, как уровень затрат (в материальном или стоимостном выражении) на восстановление работоспособности системы при реализации выделенных рисков. Исходя из экспертно определенных данных о рисках по каждому из L выделенных направлений, можно минимизировать риски его кризисного функционирования и/или состояния путем расчета оптимального уровня осуществляемых затрат (как ограниченного сверху финансового ресурса) на мероприятия по устранению (избежанию) рисков. Пусть заданы (найдены) невозрастающие зависимости rl = fl(x) рисков ri кризисного развития системы в l-м направлении (l = 1,…,L) обеспечения безопасности от затрат на их устранение (избежание, исключение, уменьшение). В случае линейности функций fl возникает возможность строить линейные оптимизационные модели функционирования ФПИ, алгоритмы численного анализа которых хорошо разработаны, что, в свою очередь, дает возможность разрабатывать системы поддержки принятия решений в практически значимых диапазонах размерностей искомых переменных.
Введем следующие обозначения:
xk (k = 1,…,n) – инвестиции в k-й проект портфеля, д.е.;
xn+k (k = 1,…,n) – потенциальный стоимостной объем производства продукции в k-м проекте фонда, д.е.;
x2n+l (l = 1,…,L) – затраты менеджмента на избежание (устранение) l-го риска функционирования ФПИ, д.е.;
Т – горизонт планирования деятельности ФПИ, ед. времени;
r – ставка дисконтирования на горизонте планирования ФПИ, %;
xk (k = 1,…,n) – эффективность (рентабельность, фондоотдача) k-го проекта, %;
tk (k = 1,…,n) – момент начала k-го проекта, ед. времени;
Tk (k = 1,…,n) – момент окончания k-го проекта, ед. времени;
qk (k = 1,…,n) – емкость рынка (стоимостная оценка спроса) продукции k-го проекта, д.е.;
rk (k = 1,…,n) – ставка дисконтирования для k-го проекта, %;
ak (k = 1,…,n) – минимальный объем инвестиций в k-й проект, д.е.;
bl (l = 1,…,L) – максимальные издержки, которые несет менеджмент ФПИ в случае реализации риска на l-ом рисковом направлении функционирования, д.е.;
cl (l = 1,…,L) – задаваемые экспертно коэффициенты, имеющие смысл оценочной значимости эффекта от осуществленных затрат на l-ом рисковом направлении функционирования, д.е.;
s – ежегодное вознаграждение менеджерам управляющей компании за управление активами ФПИ – доля от первоначальной стоимости инвестиций, %;
γ – экспертная оценка доли суммарных инвестиций, используемых менеджментом на страхование деятельности ФПИ, %;
LMAX – максимальные затраты на избежание (устранение) всех выделенных рисков функционирования ФПИ, д.е.;
I – максимальный объем инвестиций (финансовая емкость портфеля), д.е.
Тогда модель портфеля ФПИ, в форме задачи линейного программирования (ЗЛП), принимает вид
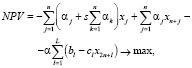 (1)
(1)
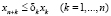 , (2)
, (2)
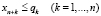 , (3)
, (3)
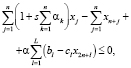 (4)
(4)
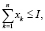 (5)
(5)
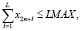 (6)
(6)
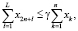 (7)
(7)
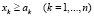 , (8)
, (8)
где параметры
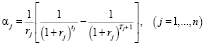
– ставки дисконтирования каждого из проектов портфеля, с учетом разновременности их начала и окончания;
α = Т/(1 + rэ) – коэффициент дисконтирования на горизонте Т;
rэ = rT/(1 – (1 + r)-T) – 1 – эффективная ставка дисконтирования на горизонте Т, в предположении равномерности распределения суммарных затрат менеджмента на избежание (устранение) рисков функционирования ФПИ на горизонте Т.
Модель (1)–(8) является частным случаем модели инвестиционно-производственных систем, опубликованной в работе [9]. В частности, в модели (1)–(8), по сравнению с моделью в работе [9], не учитываются инновационный характер инвестиционно-производственных проектов (ИПП), взаимодействие системы ИПП с ее налоговым окружением, производственная деятельность ИПП в портфеле описывается агрегированными показателями фондоотдачи δk (k = 1,…,n), не подразумевая подробного описания характеристик основных производственных фондов.
Условие (1) в данной модели является критерием эффективности портфеля ФПИ. Неравенства (2), (3) ограничивают потенциальный уровень производства в каждом проекте либо возможностями основных средств (уровнем научно-технического прогресса) либо емкостью рынков продукции. Неравенство (4) описывает условие финансовой реализуемости портфеля ФПИ. Неравенство (5) является интегральным ограничением на максимальную финансовую емкость ФПИ, (6) – ограничение на максимальные затраты для устранения рисков функционирования ФПИ, (7) – условие ограниченности суммарных затрат на страхование рисков заданной долей финансовой емкости ФПИ, а (8) является естественным условием как минимум неотрицательности инвестиций в каждый проект. Следует отметить, что параметры эффективности δk (k = 1,…,n) каждого проекта в ФПИ могут (при необходимости или наличии статистической базы) трактоваться как фондоотдачи проектов соответствующих производств, выраженные через такие рыночные и производственные характеристики активов, как средние значения стоимостей и производительностей единицы используемых производственных активов, а также средние значения стоимостей единицы продукции. Это, в частности, расширяет возможности формирования информационной базы для уточнения значений параметров δk проектов портфеля ФПИ. Наличие последней группы слагаемых в критерии (1) можно трактовать как снижение эффективности ФПИ в результате проведения страховых мероприятий на всем горизонте планирования. Эта же группа слагаемых в условии (4) трактуется, как снижение возможностей финансовой реализуемости портфеля ФПИ за счет использования страховых мероприятий на всем горизонте планирования. Отметим, что в модели (1)–(8) существование решения не гарантировано, однако, с помощью параллельного переноса системы координат в ее начало легко доказать существование решения для всех допустимых значений переменных и параметров модели. Приведенная выше модель представляет собой многопараметрическую задачу линейного программирования, при решении которой определяются такие оптимальные объемы инвестиций в проекты портфеля ФПИ, что дисконтированное по каждому проекту суммарное сальдо доходов и расходов имеет максимальное значение. Отметим, что линейность указанной модели позволяет использовать специализированный пакет инвестиционного анализа, подробно описанный в работе [5].
В модели (1)–(8) учтены такие особенности ФПИ, отличающие его от портфеля финансовых активов, как наличие ограничений на уровень спроса на производимую продукцию, возможности учета производственных особенностей и определения оптимальных характеристик проектов портфеля ФПИ в связи с наличием вспомогательной группы искомых переменных xn+k (k = 1,…,n), а также соответствующей трактовки показателей эффективности проектов. Отметим, что ставки дисконтирования rj (j = 1,…,n) традиционно учитывают инфляционные риски и риски требований внешних инвесторов. Таким образом, предложенная модель через сложную структуру дисконтирующих множителей учитывает влияние продолжительности операций по проектам, что, по нашему мнению и мнению авторов работы [10, с. 175], является важным условием обоснованности и адекватности моделей данного класса.
Следует отметить, что предложенный выше подход концептуально может быть обобщен на случай иных организаций финансового сектора экономики. В частности, для коммерческого банка в условиях финансового кризиса также являются критическими вопросы оценки устойчивости и выработки стратегии развития. Модели стратегического планирования позволяют с системных позиций анализировать финансовое состояние коммерческого банка, определять и всесторонне обосновывать пути развития, оценивать эффективность собственных вложений, а также необходимость и возможности инвестиционных вложений. Особенностями используемых моделей организаций финансового сектора является принципиальная возможность построения линейных производственных функций банка и других организаций от параметров затрат на осуществление кредитных и депозитных операций, что позволяет представить ее в форме многопараметрической задачи линейного программирования и также обеспечивает эффективную поддержку принятия решений. В Кемеровском институте (филиале) Российского экономического университета имени Г.В. Плеханова разработано программное обеспечение (ПО) поддержки принятия решений в сфере анализа проектов развития организаций финансового сектора, позволяющее, в частности, определять параметры стратегического развития коммерческого банка с учетом страхования его деятельности. Указанное ПО базируется на использовании моделей линейного оптимального управления, в которых описываются ограничения и критерии деятельности банка, осуществляющего кредитно-депозитные операции, несущего затраты на их обслуживание, страхование, котирующего свои ценные бумаги на межбанковском рынке, ограниченного в своей деятельности определяемыми государством или рыночным окружением пороговыми значениями показателей ликвидности активов, неснижаемой суммы резервов, ставки рефинансирования и т.п. Это дает возможности решать задачи управления состоянием ликвидности банковских активов, оптимизации затрат на осуществление кредитных и депозитных операций в зависимости как от внутренней банковской среды (соотношение процентных ставок кредитов и депозитов), так и от внешней для банка среды (котировки ценных бумаг банка на фондовом рынке, норма обязательного резервирования и т.п.).
Класс модели и наличие ориентированной на конечного пользователя системы автоматизации обработки информации позволяют эффективно применять данный инструментарий в условиях ситуационных центров социально-экономического развития для экспертной поддержки принятия управленческих решений по вложениям инвестиционных средств в различные организации финансового сектора экономики.
Таким образом, в статье предложена оптимизационная экономико-математическая модель оценки эффективности фондов прямых инвестиций в форме, позволяющей, при наличии разработанного автоматизированного численного инструментария [5], осуществлять эффективную поддержку принятия инвестиционных решений в условиях реально функционирующих ФПИ.
Библиографическая ссылка
Емохонова Ю.М., Медведев А.В., Победаш П.Н., Федулова Е.А. ОПТИМИЗАЦИОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОРТФЕЛЯ ФОНДА ПРЯМЫХ ИНВЕСТИЦИЙ // Фундаментальные исследования. 2018. № 2. С. 72-76;URL: https://fundamental-research.ru/ru/article/view?id=42077 (дата обращения: 03.03.2026).



