Последние десятилетия характеризуются интенсивным использованием прибрежных районов морей и океанов в экономической и хозяйственной сферах деятельности страны. Изучение гидродинамических процессов прибрежных акваторий связано с исследованием влияния волновых процессов, генерируемых в открытом море или в самой прибрежной зоне водоема. Движение волн может привести к негативным результатам, оказывающим влияние на эксплуатацию как самой прибрежной зоны, так и непосредственно объектов прибрежной инфраструктуры: к трансформации донной поверхности, происходящей вследствие подъема донных отложений, к абразии, то есть процессу разрушения волнами и прибоем берегов различных водных систем.
Проблемы защиты объектов прибрежной инфраструктуры являются чрезвычайно важными в условиях современной действительности. Результатом взаимодействия волн с донной поверхностью, береговым склоном и объектами прибрежной инфраструктуры является рефракция, дифракция и изменения структуры волн. Возведение берегозащитных сооружений, волнорезов и волновых молов в настоящее время является дорогим и сложно реализуемым техническим процессом. Ключевым требованием к проектированию берегозащитных сооружений становится исследование и анализ природных условий и факторов, в которых они будут эксплуатироваться. При этом наиболее существенными факторами являются колебания уровня поверхности воды, ветровые явления, течения, транспорт донных материалов и непосредственно деформация берегового склона.
Изучение разнообразных этапов эволюции волн, в том числе их непосредственного выхода на берег, порождает необходимость разработки комплекса взаимосвязанных математических моделей, способных достаточно точно описать данные гидродинамические процессы. Активное развитие в области математического моделирования волновых процессов и их численной реализации направлено на точное предсказание приливов, определение адекватного тренда штормовых нагонов [1].
Характерной особенностью прибрежных акваторий является значительное влияние донной поверхности на волновые процессы, что затрудняет исследование приливных явлений в прибрежных районах морей и устьях рек. Влияние волновых процессов на прибрежную зону может иметь амбивалентный характер: волновые процессы могут оказывать существенное влияние на аккумуляцию и абразию береговой зоны водоема и непосредственно на прибрежные конструкции [2].
Для моделирования гидродинамических процессов актуализируется проблема практического применения вычислительно-эффективных методов, позволяющего получать довольно точное приближенное численное решение. Таким образом, в настоящее время актуализируется необходимость построения комплекса взаимосвязанных моделей трехмерных волновых процессов и транспорта наносов, предназначенного для моделирования волновых процессов при наличии объектов прибрежной инфраструктуры.
Целью нашего исследования является разработка комплекса взаимосвязанных моделей трехмерных волновых процессов и транспорта наносов, предназначенного для моделирования волновых процессов с учетом объектов прибрежной инфраструктуры и оценка воздействия на объекты прибрежной инфраструктуры при наличии поверхностных гравитационных волн.
Поставленная цель требует реализации следующих задач: обосновать актуальность решаемой проблемы; выполнить обзор существующих подходов к проблеме; провести анализ существующих моделей транспорта наносов в водных экосистемах; проанализировать подходы к математическому моделированию данных процессов в водных экосистемах, провести классификацию описывающих их математических моделей; разработать модель транспорта донных материалов в прибрежных акваториях, предназначенную для определения динамики донной поверхности; разработать комплекс взаимосвязанных моделей трехмерных волновых процессов и транспорта веществ, предназначенного для моделирования гидродинамических волновых процессов при наличии объектов прибрежной инфраструктуры.
Математическая модель транспорта донного материала
Исходными уравнениями математической модели транспорта донных веществ являются уравнения, описывающие переформирование прибрежного рельефа [3]:
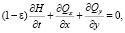
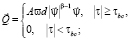
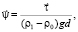 (1)
(1)
где Н – глубина дна, отсчитываемая от невозмущенной поверхности водоема; ε – пористость грунта; 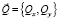 – расход наносов,
– расход наносов, 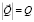 ; x, y – горизонтальные декартовы координаты; τb – касательное напряжение на дне; τbc – критическое значение касательного напряжения, при котором начинается перемещение наносов, g – ускорение свободного падения, ρ – плотность жидкости, А и β – безразмерные постоянные (А равно 19,5, β равно 3), ω – частота волны, d – характеристика осадков.
; x, y – горизонтальные декартовы координаты; τb – касательное напряжение на дне; τbc – критическое значение касательного напряжения, при котором начинается перемещение наносов, g – ускорение свободного падения, ρ – плотность жидкости, А и β – безразмерные постоянные (А равно 19,5, β равно 3), ω – частота волны, d – характеристика осадков.
Принимая во внимание ограничения на касательные напряжения на дне расчетной области, система уравнений (1) может быть представлена в виде [4]:
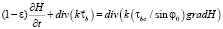 , (2)
, (2)
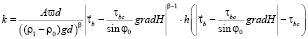 , (3)
, (3)
где 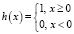 – функция Хэвисайда.
– функция Хэвисайда.
Уравнение (2) дополняется начальным и граничным условиями:
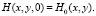 (4)
(4)
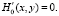 (5)
(5)

Рис. 1. Начальный рельеф дна

Рис. 2. Геометрия дна через 80 минут
Для расчета тангенциальных напряжений в модели транспорта наносов необходима информация о поле вектора скорости на дне водоема [5].
Рис. 1–2 иллюстрируют результаты численных экспериментов моделирования динамики донной поверхности. При этом размер расчетной сетки равен 200×200, шаг по пространственным переменным 0,1 м, шаг по времени 0,01 с, скорость движения ветра 5 м/с и направлена слева направо.
Математическая модель волновой гидродинамики
Для математического описания задачи волновой динамики жидкости использована модель [6], представленная на рис. 3.
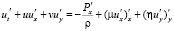 , (6)
, (6)
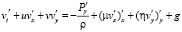 , (7)
, (7)
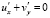 . (8)
. (8)
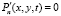 ,
, 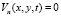 ,
,
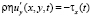 ,
, 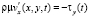 , (9)
, (9)
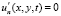 ,
, 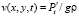 ,
,
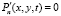 , (10)
, (10)
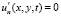 ,
, 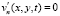 ,
,
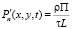 , (11)
, (11)
где 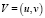 – вектор скорости движения водной среды; Р – давление; μ, η – коэффициенты турбулентного обмена по горизонтальному и вертикальному направлениям соответственно; g – ускорение свободного падения; ρ – плотность жидкости; τx, τy – составляющие тангенциального напряжения на дне жидкости; П – поток вектора скорости через боковую поверхность; L – расстояние от поверхности жидкости до дна (глубина жидкости с учетом возвышения уровня) на боковой границе. Система координат выбрана таким образом, что ось Ox совмещена с поверхностью невозмущенной жидкости и направлена в сторону берега, ось Oy – вертикально вниз.
– вектор скорости движения водной среды; Р – давление; μ, η – коэффициенты турбулентного обмена по горизонтальному и вертикальному направлениям соответственно; g – ускорение свободного падения; ρ – плотность жидкости; τx, τy – составляющие тангенциального напряжения на дне жидкости; П – поток вектора скорости через боковую поверхность; L – расстояние от поверхности жидкости до дна (глубина жидкости с учетом возвышения уровня) на боковой границе. Система координат выбрана таким образом, что ось Ox совмещена с поверхностью невозмущенной жидкости и направлена в сторону берега, ось Oy – вертикально вниз.
Для численной реализации дискретной модели задачи волновой гидродинамики введена сетка:
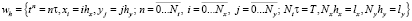 ,
,
где τ – шаг по времени, hx, hy – шаги по пространству, Nt – верхняя граница по времени, Nx, Ny – границы по пространству.
Рис. 4 иллюстрирует трансформацию профиля волны, набегающей на берег, с течением времени, программа отображает векторы поля скорости, градацией цвета показано поле давления.
Математическая модель волновых процессов, учитывающая наличие надводных береговых сооружений
Для разработки математической модели движения водной среды использована трехмерная гидростатическая модель, представленная на рис. 5.
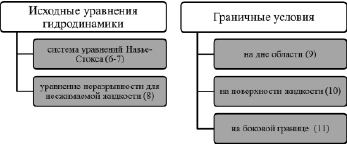
Рис. 3. Исходные уравнения математической модели волновой гидродинамики
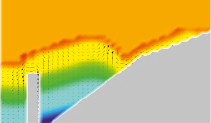
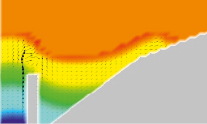
Рис. 4. Динамика профиля уровня возвышения жидкости при наличии прибрежной конструкции
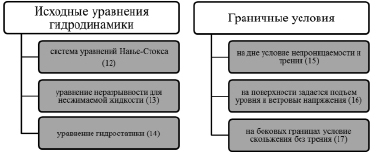
Рис. 5. Исходные уравнения математической модели волновых процессов, учитывающей наличие надводных береговых сооружений
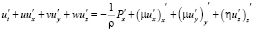 ,
,
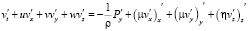 , (12)
, (12)
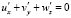 , (13)
, (13)
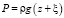 . (14)
. (14)
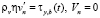 ,
, 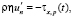 (15)
(15)
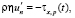
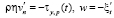 , (16)
, (16)
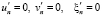 , (17)
, (17)
где ξ – функция подъема уровня (функция возвышения), 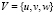 – вектор скорости движения водной среды, Р – давление,
– вектор скорости движения водной среды, Р – давление,
μ, η – коэффициенты турбулентного обмена по горизонтальному и вертикальному направлениям соответственно, g – ускорение свободного падения, ρ – плотность жидкости, τx, τy – тангенциальное напряжение на дне жидкости, оси Ox, Oy имеют горизонтальное направление.
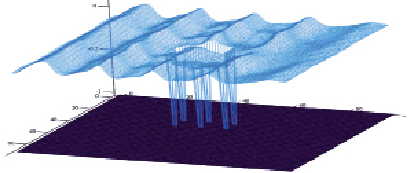
Рис. 6. Функция возвышения уровня при обтекании водной средой прибрежного объекта
Для расчета давления в гидростатическом приближении при наличии надводного объекта, установленного на дне водоема, используем уравнение
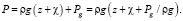
Функция возвышения в этом случае примет вид
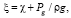
где χ – функция, описывающая геометрию дна.
Взаимосвязанный комплекс программ был использован для расчета гидродинамического воздействия волновых процессов на прибрежный объект. Размеры подводной части конструкции: 5 м×10 м×20 см. Объект установлен на шести опорах. Зона моделирования имеет размеры 50 м×50 м×1 м (рис. 6).
Результаты численных экспериментов, полученные с помощью применения взаимосвязанного комплекса программ по моделированию гидродинамических волновых процессов, позволяют провести оценку воздействия волновых процессов на прибрежные объекты.
Заключение
Оценка гидродинамического воздействия на берегозащитные сооружения и прибрежные конструкции, установленные на дне мелководного водоема, является важнейшей задачей в настоящее время, применение результатов исследований, представленных в статье, связано с планированием рационального природопользования.
Новизна научной идеи состоит в применении комплекса взаимосвязанных моделей волновых процессов и транспорта донных материалов в прибрежных акваториях с учетом наличия объектов прибрежной инфраструктуры, а также воздействия на объекты прибрежной инфраструктуры при наличии поверхностных волн. Разработанный комплекс взаимосвязанных моделей волновых процессов и транспорта донных материалов может быть использован при планировании целесообразного природопользования и прогнозировании динамики донной поверхности.
Работа выполнена при поддержке РНФ (проект № 17–11–01286).
Библиографическая ссылка
Чистяков А.Е., Проценко Е.А., Тимофеева Е.Ф., Николич Н.А. МОДЕЛИРОВАНИЕ ВОЛНОВЫХ ПРОЦЕССОВ И ТРАНСПОРТА ДОННЫХ МАТЕРИАЛОВ С УЧЕТОМ НАЛИЧИЯ ПРИБРЕЖНЫХ КОНСТРУКЦИЙ В ПРИБРЕЖНЫХ АКВАТОРИЯХ // Фундаментальные исследования. 2017. № 12-1. С. 157-162;URL: https://fundamental-research.ru/ru/article/view?id=41996 (дата обращения: 14.02.2026).



