Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Цимбал В.А. 1 Тоискин В.Е. 1 Лягин М.А. 1

---

1 Военная академия РВСН имени Петра Великого филиал

Рассматривается асимметричный радиотракт передачи данных типа «точка – точка», включающий прямое и обратное направления, которые однородны по вероятности битовой ошибки. При этом в данном тракте реализован протокол доставки многопакетных сообщений типа Х.25 с кумулятивной квитанцией. Многопакетное сообщение на передающей стороне разделяется на совокупность пакетов, а на приемной стороне данная совокупность пакетов объединяется в общее сообщение, выдаваемое получателю. Квитирование совокупности принятых пакетов осуществляется по обратному каналу кумулятивной квитанцией. На основе поглощающих конечных марковских цепей строится математическая модель процесса доставки многопакетного сообщения произвольного размера по данному радиотракту передачи данных, учитывающая все системные параметры прямого и обратного каналов. На этой основе находятся вероятностно-временные характеристики процесса доставки, характеризующие свойство своевременности. При этом искомый процесс описывается ситуационными двудольными графами, которые учитывают количество передаваемых кадров, количество повторов каждого кадра, применение способа «скользящего окна» и при этом содержат два поглощающих состояния: состояние доведения и состояние недоведения. Показывается, что такой тип графа позволяет получать вероятности поглощающих состояний в аналитическом виде, что, в свою очередь, позволяет применять известные методы оптимизации параметров процесса доставки при ограничениях заказчика на вероятностно-временные характеристики при минимальных скоростных затратах прямого и обратного каналов рассматриваемого радиотракта. В ходе исследований показано, что разработанный научно-методический аппарат адекватно описывает процесс доставки многопакетных сообщений в рассматриваемой системе передачи данных, работающей по протоколу типа Х.25 с кумулятивной квитанцией, и позволяет найти границы применимости данного протокола.

Статья в формате PDF

0 KB

протокол Х.25

информационный обмен

система передачи данных

решающая обратная связь

многопакетное сообщение

кумулятивная квитанция

границы применимости

1. Цимбал В.А. Информационный обмен в сетях передачи данных. Марковский подход: монография. – М.: Вузовская книга, 2014. – 144 с.

2. Цимбал В.А., Тоискин В.Е., Шиманов С.Н. Математическая модель процесса информационного обмена по протоколу ТСР на основе теории конечных марковских цепей [Текст] //Электросвязь. – 2015. – № 11. – С. 53–58.

3. Бусленко Н.П. Исследование сложных технических систем. – М.: Наука, 1982. – 250 с.

4. Олифер В.Г., Олифер Н.А. Компьютерные сети. Принципы, технологии, протоколы. – СПб.: Питер, 2012. – 944 с.

5. Цимбал В.А., Хоптар В.В., Сорокин О.И., Лягин М.А., Бережной А.А., Крючков Н.В. Правила автоматизированного синтеза конечной марковской цепи, описывающей доведение многопакетного сообщения в соединении «точка-точка» [Текст] // «Наука. Инновации. Технологии» Научный журнал Северо-Кавказского федерального университета. – 2016. – Вып. 4. – С. 91–98.

6. Кемени Дж. Дж., Снелл Дж. Ларк. Конечные цепи Маркова // Пер. с англ. – М.: Наука, 1970. – 272 с.

7. Вентцель Е.С. Теория вероятностей. – М.: Наука, 2003. – 564 с.

8. Казаков В.А. Введение в теорию марковских процессов и некоторые радиотехнические задачи – М.: Сов. Радио, 1973. – 232 с.

9. Баврин И.И., Матросов В.А. Общий курс высшей математики: учеб. для студентов физ.-мат. спец. пед. вузов. – М.: Просвещение, 1995. – 464 с.

10. Босс В. Лекции по математике. Т. 7: Оптимизация: учеб. пособие. Изд. 3-е. – М.: книжный дом «Либроком», 2010. – 216 с.

В данном исследовании рассматривается радиотракт передачи данных направления «борт – земля», предназначенный для доставки с беспилотного летательного аппарата (БПЛА) дискретного сообщения значительной ёмкости в центр управления полетами (ЦУП), причем доставка должна быть реализована с высокой своевременностью, оцениваемой вероятностно-временными характеристиками (ВВХ). Отметим, что под ВВХ понимается вероятность доставки фиксированного объема информации за время, не превышающее заданное [1–4].

Рассматриваемый радиотракт является двусторонним, содержащим прямой и обратный канал передачи данных (КПД), при этом по прямому КПД передаются пакеты (кадры), а по обратному – кумулятивные квитанции на совокупности успешно принятых пакетов (кадров). Длина кадра Lк гораздо больше длины квитанции Lкв, поэтому прямой КПД должен быть высокоскоростным, а обратный КПД – низкоскоростным. Таким образом, рассматриваемый радиотракт является асимметричным трактом передачи данных (АТПД) [4, 5].

Ставится и решается задача нахождения минимально достаточных скоростей в прямом и обратном АТПД, обеспечивающих заданные ВВХ доставки объема информации I, представленного в виде МПС. Формальная постановка задачи имеет вид

Найти:

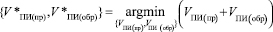(1)

при ограничениях на ВВХ доведения МПС общей емкостью I бит,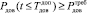

где 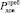– требуемая вероятность доведения МПС; – допустимое время доведения МПС; 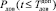– вероятность доведения МПС за время, не превышающее .

Использование кумулятивной квитанции предусматривает использование «скользящего окна», под которым понимается количество кадров (пакетов), которое можно передать без квитирования в зависимости от помеховой обстановки. Согласно ГОСТ Р. 34.950-92 в протоколе Х.25 предусматриваются различные факультативные услуги, позволяющие на пакетном уровне синтезировать систему передачи данных (СПД), по ВВХ удовлетворяющую требованиям заказчика. Перед сеансом связи между абонентами происходит согласование параметров управления потоком, которыми являются размер пакета и размер окна («скользящего окна»). Использование данной факультативной услуги доступно на определенный период времени для виртуальных соединений (если она абонирована). По умолчанию стандартным значением размера окна в рассматриваемом протоколе является u = 2 кадрам. Также существует возможность установки нестандартных значений окна при использовании соответствующей факультативной услуги. Значения, отличные от рекомендуемых размеров окна, могут быть согласованы для каждого виртуального соединения. В нашем случае таковыми виртуальными соединениями являются прямой и обратный КПД. В данном исследовании длина «скользящего окна» равна usk = 5. Количество повторов каждого передаваемого кадра – g = 1 и g = 3.

Теоретической основой для исследования процесса доставки многопакетного сообщения (МПС) по протоколу Х.25 с кумулятивной квитанцией фиксированной величины приняты поглощающие конечные марковские цепи (ПКМЦ) [5–7]. При этом для описания искомого процесса используются ситуационные двудольные графы, содержащие совокупность переходных состояний и два поглощающих состояния, одно из которых является состоянием недоведения сообщения (неуспеха), а второе – состоянием доведения сообщения (успеха) [8]. Для удобства пользования таким подходом в исследовании приняты следующие обозначения для анализируемой СПД: «usk -u-g», где usk – размер «скользящего окна»; u – количество кадров, на которое делится исходный массив информации; g – допустимое количество повторов каждого передаваемого кадра.

Для решения задачи (1) рассмотрим СПД типа 5-5-1, в которой используется «скользящее окно» длиной в пять кадров, доставка которых квитируется кумулятивной квитанцией. При этом обозначим БПЛА как ЗПД-отправитель, а ЦУП как ЗПД-получатель.

Ситуационный двудольный граф, отображающий процесс доставки пятипакетного МПС с кумулятивной квитанцией, представлен на рис. 1. Семантика состояний этого графа, такова: S1 – ЗПД-отправитель выдало пять кадров, которые на ЗПД-получателе не приняты; S2 – ЗПД-получатель приняло переданные пять кадров и выдало в ответ кумулятивную квитанцию; S3 – ЗПД-получатель приняло четыре из пяти переданных кадров и выдало в ответ кумулятивную квитанцию; S4 – ЗПД-получатель приняло три из пяти переданных кадров и выдало в ответ кумулятивную квитанцию; S5 – ЗПД-получатель приняло два из пяти переданных кадров и выдало в ответ кумулятивную квитанцию; S6 – ЗПД-получатель приняло один из пяти переданных кадров и выдало в ответ кумулятивную квитанцию; S7 – фиктивное состояние, обозначающее завершение времени передачи пяти очередных кадров и переход к покадровой передаче; S8 – ЗПД-отправитель выдало очередной кадр из пяти оставшихся, которые на ЗПД-получателе не приняты; S9 – ЗПД-получатель приняло очередной кадр и выдало в ответ кумулятивную квитанцию; S10 – фиктивное состояние, обозначающее завершение времени передачи очередного кадра; S11 – ЗПД-отправитель выдало кадр из четырех оставшихся, которые на ЗПД-получателе не приняты; S12 – ЗПД-получатель приняло очередной кадр и выдало в ответ кумулятивную квитанцию; S13 – фиктивное состояние, обозначающее завершение времени передачи очередного кадра; S14 – ЗПД-отправитель выдало очередной кадр из трех оставшихся, которые на ЗПД-получателе не приняты; S15 – ЗПД-получатель приняло очередной кадр и выдало в ответ кумулятивную квитанцию; S16 – фиктивное состояние, обозначающее завершение времени передачи очередного кадра; S17 – ЗПД-отправитель выдало очередной кадр из двух оставшихся, которые на ЗПД-получателе не приняты; S18 – ЗПД-получатель приняло очередной кадр и выдало в ответ кумулятивную квитанцию; S19 – фиктивное состояние, обозначающее завершение времени передачи очередного кадра; S20 – ЗПД-отправитель выдало последний оставшийся кадр, который на ЗПД-получателе не принят; S21 – ЗПД-получатель приняло очередной кадр и выдало в ответ кумулятивную квитанцию; S22 – фиктивное состояние, обозначающее завершение времени передачи очередного кадра; S23 – ЗПД-отправитель квитанцию не получило, канал, по которому была передача, бракуется; S24 – ЗПД-отправитель квитанцию получило, передача кадров завершена.

В рассматриваемом графе состояния S7, S10, S13, S16, S19, S22, являются фиктивными, и вероятности перехода в последующие из них состояния определяются так: р78 = р1023 = р1323 = р1623 = р1923 = р2223 = 1. При этом в рассматриваемом графе недоведению кадра соответствует состояние S23, а доведению кадра – состояние S24.

Вероятность доставки одного кадра за один повтор, а также вероятность доведения квитанции о правильности доставки переданных кадров рассчитываются по следующим формулам [8, 9]:

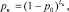(2)

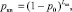(3)

где Lк – длина кадра, Lкв – длина кумулятивной квитанции. Отметим, что помехоустойчивое кодирование здесь не учитывается, что не влияет на общность подхода.

Переходные вероятности МПВ находятся так. Переход из состояния S1 в состояние S2 возможен тогда, когда пять кадров, переданные ЗПД-отправителем, получены на приемной стороне. Вероятность такого события равна: .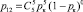

Переход из состояния S1 в состояние S3 возможен тогда, когда четыре из пяти кадров, переданных ЗПД-отправителем, получены на приемной стороне. Вероятность такого события равна: 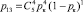. Переход из состояния S1 в состояние S4 возможен тогда, когда три из пяти кадров, переданных ЗПД-отправителем, получены на приемной стороне. Вероятность такого события равна: 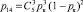. Переход из состояния S1 в состояние S5 возможен тогда, когда два из пяти кадров, переданных ЗПД-отправителем, получены на приемной стороне. Вероятность такого события равна: 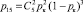. Переход из состояния S1 в состояние S6 возможен тогда, когда один из пяти кадров, переданных ЗПД-отправителем, получен на приемной стороне. Вероятность такого события равна: 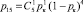. Переход из состояния S1 в состояние S7 возможен тогда, когда ни один из пяти кадров, переданных ЗПД-отправителем, не получен на приемной стороне. Вероятность такого события равна: .

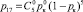Вероятности успеха рк и неуспеха qк доставки очередного пакета без использования «скользящего окна», а также доведения ркв (недоведения qкв) кумулятивных квитанций находятся по формулам (2) и (3):

р89 = р1112 = р1415 = р1718 = р2021 = рк,

р810 = р1113 = р1416 = р1719 = р2022 = qк,

р911 = р1214 = р1517 = р1820 = р2124 = ркв,

р923 = р1213 = р1523 = р1823 = р2123 = qкв.

Таким образом, можно рассчитать все компоненты МПВ. Время, которое затрачивается на передачу одного кадра и одной квитанции, находится по формулам

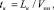(4)

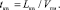(5)

Времена шагов переходов по графу данной ПКМЦ с учетом формул (4) и (5) находятся так:

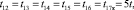
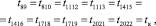
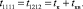
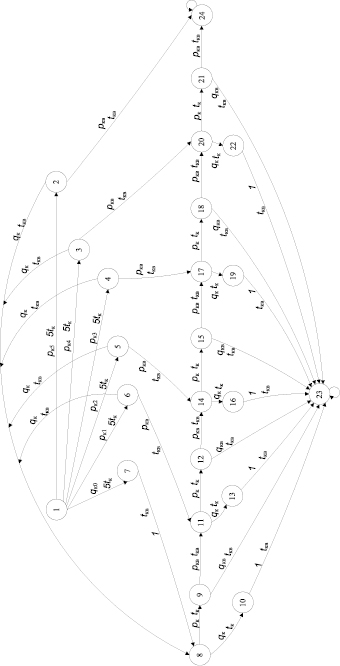
Рис. 1. Ситуационный двудольный граф типа 5-5-1, отображающий процесс доставки пятипакетного МПС с квитированием по кумулятивной квитанции

Значения времен переходов, равных tкв, будут следующими: t28, t38, t48, t58, t68, t78, t224, t320, t417, t514, t611, t28, t911, t923, t1214, t1223, t1517, t1523, t1820, t1823, t2124, t2123, t1023, t1323, t1623, t1923, t2223.

ВВХ доставки пятипакетного МПС определяются в ходе решения уравнения Колмогорова – Чепмена (УКЧ) [1]:

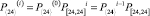, (6)

где

,

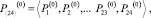
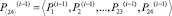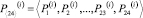– векторы вероятностей состояний процесса на нулевом шаге, (i-1)-м и i-м шагах соответственно; P[24, 24] – матрица переходных вероятностей (МПВ).

Подчеркнем, что в векторе вероятностей состояний вероятность P23 есть вероятность неуспеха, а вероятность P24 есть вероятность успеха.

Для численных расчетов ВВХ примем следующие исходные данные: длина кадра изменяется в пределах Lк = 64…1000 бит, длина квитанции фиксирована на сеансе связи и равна Lкв = 24 бита, количество кадров в передаваемом МПС равно 5, требуемые ВВХ доставки равны: 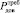= 0,995, = 20 с, вероятности битовой ошибки в прямом и обратном КПД варьируются в пределах 10-7… 5*10-4.

Оптимизационная задача (1) решается методом неопределенных множителей Лагранжа [8–10]. Искомые скорости в прямом и обратном каналах как результат ее решения имеют вид

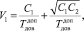(7)

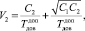(8)

где C1 = u_sk·L_к + (К1 – 1)·L_к – объем информации в совокупности кадров, передаваемой по прямому КПД, C2 = К₂·L_кв – объем информации в совокупности квитанций, передаваемой по обратному КПД рассматриваемого АТПД. При этом К1 есть число передач пакета, а К2 есть число передач квитанции в ходе доставки МПС с заданными ВВХ. Данные величины находятся по приведенной модели доставки МПС.

Необходимо отметить, что выражение для С1 учитывает особенность использования кумулятивной квитанции, а именно длину первого шага процесса, которое по времени равно передаче числа кадров, равных длине «скользящего окна».

Описанный подход позволяет решить задачу (1) и для случая передачи МПС с большим, чем 5, числом пакетов. Пусть при этом общее МПС будет разбито, например, на m сегментов по 5 пакетов. Требование по вероятности доведения к одному пятипакетному МПС будет определяться из выражения 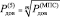. А требования по времени доведения к одному пятипакетному МПС будут определяться из выражения: .

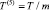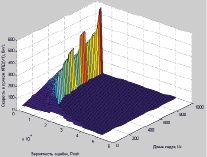
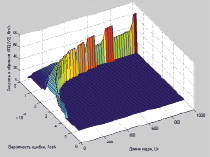
а) б)

Рис. 2. Трехмерный график зависимости скорости передачи информации по прямому (а) и обратному (б) КПД от вероятности битовой ошибки и длины кадра (пакета) в СПД типа 5-5-1

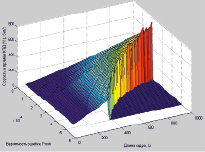
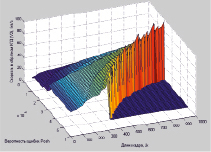
а) б)

Рис. 3. Трехмерный график зависимости скорости передачи информации по прямому (а) и обратному (б) КПД от вероятности битовой ошибки и длины кадра (пакета) в СПД типа 5-5-3

Тогда величины С1’ и С2’ будут находиться так: С1’ = m·C1, С2’ = m·C₂. Именно относительно величин С1’ и С2’ и общего времени доведения Т будет решаться задача (1).

По результатам данного исследования можно сделать такие выводы:

1. Математическая модель доставки МПС с кумулятивной квитанцией по протоколу Х.25, разработанная на базе ПКМЦ в виде ситуационных двудольных графов, адекватно отображает физику исследуемого процесса, так как:

а) с течением времени вероятность доставки сообщения увеличивается;

б) с улучшением качества канала по вероятности битовой ошибки время доставки МПС уменьшается, а вероятность его доставки увеличивается.

2. Данная модель применима к описанию процесса доставки МПС сколь угодно большой емкости. При этом такое МПС следует декомпозировать на совокупность из m сегментов рассмотренной пакетной емкости.

3. Сформулирована и решена задача нахождения минимально достаточных скоростей в прямом и обратном КПД асимметричного радиотракта передачи данных. В основу оптимизации положен метод неопределенных множителей Лагранжа.

4. Разработанный научно-методический аппарат позволяет находить границы применимости протокола типа Х.25 с кумулятивной квитанцией в асимметричном радиотракте передачи данных при требуемой достоверности и оперативности доставки многопакетного сообщения (рис. 2 и 3).

5. Описанный подход может быть внедрен в программное обеспечение контроллера формирователя кадра ЗПД-отправителя и ЗПД-получателя и должен использоваться на стадии эксплуатации АТПД для настройки сеансовых параметров перед началом информационного обмена.

Библиографическая ссылка