Основной недостаток алгоритмов поиска объектов на изображениях, полученных после операции выделения контуров, состоит в их неспособности надежно разделять контуры по отдельным объектам. Объекты могут быть составными или перекрываться. Такая конфигурация может вносить значительные искажения в описания контуров объектов, и в результате информация, необходимая для распознавания объекта, окажется в нескольких несвязанных цепочках контуров.
Для наглядности основные возможные сложности для алгоритма, ищущего прямоугольные объекты на изображении, собраны в одном синтезированном изображении и пронумерованы (рис. 1).
Варианты расположения объекта на изображении:
1. Контакт с областью другого цвета.
2. Небольшой заслоняющий объект.
3. Разделение объекта на несколько независимых контуров вследствие перекрытия другим объектом.
4. Выход за пределы изображения.
5. Общая грань с областью другого цвета.
6. Небольшой размер (область слишком мала для надежного распознания).
7. Общая грань с областью другого цвета.
8. Контакт с другой областью того же цвета.
Подобные варианты расположения объектов с высокой долей вероятности приводят к искажению описывающих объекты контуров, что делает невозможным определение среди них искомых объектов.
Цель исследования
Целью данного исследования является создание структуры, описывающей контуры на изображении, и поиск по этой структуре объектов с определенными геометрическими особенностями. В частности, работа алгоритма рассматривается на примере поиска объектов на изображении представляющих собой плоские прямоугольные области в пространстве.
В качестве образца возможных комбинаций положения прямоугольных объектов по отношению друг к другу будет рассматриваться синтезированное изображение (рис. 1).
Контуры объектов на изображении находятся с помощью алгоритма Сузуки [1] и аппроксимируются методом Дугласа – Пекера [2]. Результат работы этих алгоритмов представлен на рис. 2.
Алгоритм выделения контуров изображения определил отдельно области 6, 5 (рис. 1), но при этом описал их два раза, по внешнему и по внутреннему краю контура. Объединил в один объект области 1 и 2 (рис. 1), при этом у области 1 остался четырехугольный внутренний контур, а на области 2 образовался набор лишних контуров. Области же 7, 8 (рис. 1) не образовали замкнутого внешнего контура вообще.

Рис. 1. Возможные комбинации положения прямоугольных объектов по отношению друг к другу
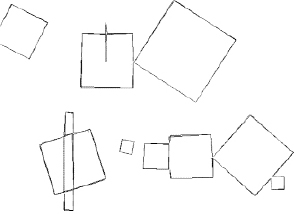
Рис. 2. Результат работы алгоритмов выделения контуров на синтезированном изображении
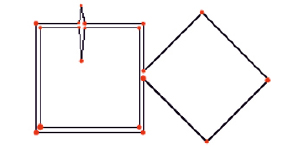
а)
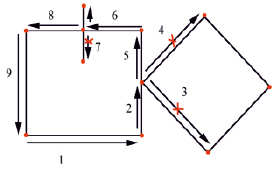
б)
Рис. 3. Контурное описание до (a) и после (б) преобразования. Порядок обхода графа при поиске объектов прямоугольной формы (б)
Для дальнейшего описания нужно объединить цепочки в единую сеть. Алгоритм должен обнаружить все близлежащие точки и связать их друг с другом. Например, контуры, образованные областями 1 и 2 (рис. 3, а), должны преобразоваться как на рис 3, б. Подобную структуру удобнее всего хранить в двусвязном графе.
Для определения «разорванных» объектов, т.е. объектов, определяемых не единственной цепочкой контуров, алгоритм объединяет все найденные цепочки контуров в единый граф. При добавлении в граф нового контура каждая его точка по очереди проверяется на близость к уже добавленным вершинам графа. В случае обнаружения таких вершин точка сливается с ранее добавленными вершинами графа и к ним добавляются только дополнительные связи. На рис. 4 представлен результат объединения в единый граф контуров объектов 1 и 2 из рис. 1. Небольшой треугольник между вершинами 1 и 2 увеличен, чтобы показать, что линия, соединяющая эти точки на самом деле описывается два раза. Подобное переопределение может затруднить поиск объектов в дальнейшем, поэтому все вершины, расположенные рядом с ребрами графа, соединяются с ними. Для каждой вершины считается расстояние до всех ребер, которым она не принадлежит, и, если растояние меньше заданного предела, вершина проецируется на ребро и разбивает его на два новых. Чтобы ускорить проверку, изображение разбивается сеткой на участки, для каждого из которых записываются ребра проходящие через него. Такой подход позволяет сократить число проверяемых ребер до нескольких единиц на каждую вершину.
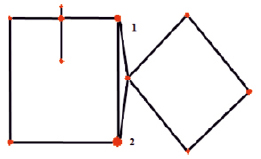
Рис. 4. Результат объединения цепочки контуров
Полученный граф будет описывать контуры исходного изображения. При этом объекты, для которых было обнаружено несколько отдельных контуров, будут полностью описываться одной областью связанности графа.
На следующем этапе работы алгоритм производит очистку графа от лишней информации. Удаляются все вершины, имеющие только одно ребро. Для сохранения информации они помечаются как «неактивные». Так же удаляются вершины, имеющие два ребра и образующие угол близкий к развернутому. Такие вершины не могут быть угловыми для четырехугольного объекта, и их анализ будет лишней тратой времени.
На получившемся графе производится поиск контуров, которые образуют на изображении четырехугольник с заданными параметрами. Искомый контур должен быть выпуклым, обладать площадью и геометрией, достаточной для стабильной работы алгоритма распознавания.
Поиск производится в глубину от каждой вершины графа. Вершины, предположительно являющиеся угловыми, записываются в стек, а остальные вершины пропускаются. После накопления четырех вершин в стеке производится попытка замкнуть образовавшийся контур. В случае успеха получившийся четырехугольник подвергается дополнительным проверкам, чтобы подтвердить его принадлежность границе плоского прямоугольного объекта.
Пример прохода алгоритма изображен на рис. 3, б. Начав из нижней левой, алгоритм пройдет к первой вершине (стрелка 1) и добавит ее в стек. Обнаружив единственную дополнительную вершину, связанную с текущей, алгоритм перейдет к ней (стрелка 2), при этом будет зафиксировано направление угла поворота. От следующей вершины отходят три дополнительных ребра. Два из них (стрелки 3 и 4) отклоняются в сторону противоположную необходимой и не смогут образовать выпуклый четырёхугольник. Оставшееся ребро идет почти параллельно ребру, по которому алгоритм пришел в эту точку (стрелка 5), и поэтому переход будет осуществлен, при этом точка записана не будет. Таким же образом алгоритм проследует по шестой стрелке, упрется в тупик, проследовав по стрелке 7, и, вернувшись назад через стрелки 8 и 9, доберется до изначальной вершины, замкнув круг (рис. 3, б).
При поиске объектов на изображении, представляющих собой плоские прямоугольные области в пространстве, наиболее важной частью является определение угла между ребрами ограничивающего контура. При проходе каждого ребра вычисляется синус угла текущего ребра с предыдущим. На основе этого принимается решение о продолжении поисков и записи вершины в стек угловых вершин. На рис. 5 демонстрируется визуальная интерпретация принятия решения.
Если новое ребро направлено в красную зону, вершина не подходит и ее можно не рассматривать дальше. Зеленая зона означает, что новое ребро можно рассматривать как продолжение старого, поиск продолжается, при этом точка принятия решения не будет включена в итоговый четырехугольник. Для желтой зоны поиск будет продолжен, при этом точка принятия решения будет считаться точкой четырехугольника.
Представленный алгоритм способен выделить плоские прямоугольники в пространстве при условии, что их границы найдены четко и не имеют разрывов больше нескольких пикселей.
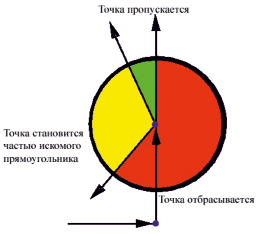
Рис. 5. Визуализация принятия решения при поиске контура
Для борьбы с разрывами в найденных границах предполагается использовать эвристические алгоритмы, основывающиеся на доопределении линий на основе близлежащих ребер графа, не относящихся к той части, на которой идет поиск (подразумевается, что доопределяющее ребро может не являться частью выделяемого объекта вообще).
Предложенный алгоритм может эффективно использоваться для поиска «информационных объектов» помещения в задаче автономной навигации в закрытых помещениях [3–6]. Это могут быть названия и номера помещений, планы эвакуации, знаки пожарной безопасности и т.д. Все эти объекты представляют собой плоские прямоугольные области в пространстве. Аналогичным образом можно производить поиск треугольных табличек. Например, знаков, предупреждающих о высоком напряжении.
Получившийся в процессе работы граф можно использовать для анализа других объектов в задаче навигации. Например, с его помощью можно существенно облегчить поиск на изображении таких объектов, как лестницы [7], коридоры и двери [8–10]. Алгоритмы поиска таких объектов, как правило, базируются на детектировании линий с использованием преобразования Хафа [11]. При этом изначально не учитывается физическое расположение линий на изображении, разрывы, препятствия, что вызывает ложные срабатывания или затрудняет детектирование. В то время как наличие уже найденных линий на изображении позволит упростить поиск этих объектов. Граф позволяет задать поиск в глубину или поиск по всем объектам с настраиваемыми фильтрами для выделения необходимых объектов, будь то линии или геометрические фигуры.
Заключение
В ходе работы разработана и реализована структура для хранения описаний контуров, исключающая лишние определения и разрывы (несколько цепочек контуров описывают один большой контур). При этом контурное изображение практически не искажается, что позволяет проводить дальнейший анализ. Разработан настраиваемый алгоритм поиска объектов на контурном описании, которые соответствуют заданным геометрическим критериям.
Работа была выполнена при поддержке гранта РФФИ № 16-07-01214 А.
Библиографическая ссылка
Патрушев А.О., Осипов М.П. ПОИСК ГРАНИЦ ОБЪЕКТОВ ПРЯМОУГОЛЬНОЙ ФОРМЫ НА ИЗОБРАЖЕНИЯХ С КОНТУРНЫМ ФОРМАТОМ ПРЕДСТАВЛЕНИЯ // Фундаментальные исследования. 2017. № 12-1. С. 91-96;URL: https://fundamental-research.ru/ru/article/view?id=41985 (дата обращения: 14.02.2026).



