Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Богданова В.Г. 1 Горский С.А. 1

---

1 Институт динамики систем и теории управления имени В.М. Матросова СО РАН

Рассматривается эффективность применения сервис-ориентированного приложения для параллельного решения задач булевой выполнимости в распределенной вычислительной среде. Для распараллеливания на подзадачи используется декомпозиция по данным с помощью метода расщепления исходной булевой функции. Приводится архитектура и функциональные возможности MPI-приложения, на основе которого реализован сервис. MPI-приложение использует стратегию «master-slave» для распределения задач по процессам. Рассматриваются факторы, влияющие на время выполнения приложения. Исследуется зависимость эффективности приложения от ряда динамических характеристик. Одной из основных обобщающих характеристик является масштабируемость приложения. Приводится зависимость масштабируемости от параметров запуска приложения – размерности задачи, количества процессорных ядер, нагрузки на дочерние процессы. Оценивается масштабируемость приложения для задач разного класса. Приводится сравнение разработанного приложения с массовым параллельным решателем HordeSat. Обсуждаются результаты вычислительных экспериментов.

Статья в формате PDF

0 KB

масштабируемость

эффективность

задача булевой выполнимости

параллельный решатель

сервис

1. Kandaswamy, Gannon D. A Mechanism for Creating Scientific Application Services Ondemand from Workflows // Proceedings of the 2006 International Conference Workshops on Parallel Processing. – 2006. – P. 25–32.

2. Теплов А.М. Об одном подходе к сравнению масштабируемости параллельных программ // Вычислительные методы и программирование. – 2014. – Т. 15, Вып. 4. – С. 697–711.

3. Бычков И.В., Опарин Г.А., Богданова В.Г., Горский С.А., Пашинин А.А. Мультиагентная технология автоматизации параллельного решения булевых уравнений в распределенной вычислительной среде // Вычислительные технологии. – 2016. – Т. 21, № 3. – С. 5–17.

4. Горшков С.П. Применение теории NP-полных задач для оценки сложности решения систем булевых уравнений // Обозрение прикладной и промышленной математики, серия дискретной математики. – 1995. – Т. 2. – Вып. 3. – С. 325–398.

5. Горский С.А., Богданова В.Г. Гибридный sat-решатель hpcsat // Информационные и математические технологии в науке и управлении: труды XIX Байкальской Всерос. конф. с междунар. участием. – Иркутск: ИСЭМ СО РАН, 2014. – С. 81–88.

6. Данцин Е.Я. Алгоритмика задачи выполнимости // Вопросы кибернетики. Проблемы сокращения перебора. – М.: АН СССР, 1987. – С. 7–29.

7. Поцелуевская Е.А. Теоретическая и практическая сложность задач выполнимости булевых формул // Интеллектуальные системы. Теория и приложения. – 2009. – Т. 13, № 1–4. – С. 455–476.

8. Balyo T., Sanders P., Sinz C. HordeSat: A Massively Parallel Portfolio SAT Solver // Theory and Applications of Satisfiability Testing – SAT 2015. Lecture Notes in Computer Science. – 2015. – Vol. 9340. – P. 156–172.

9. Хакен А. Труднорешаемость резолюций. Кибернетический сборник. Новая серия. Сб. статей за 1988-1990 г. – М.: Мир. – 1991. – Вып. 28. – 206 с.

10. HordeSat and HordeQBF – Massively Parallel SAT/QBF Solvers. URL: http://baldur.iti.kit.edu/hordesat (дата обращения: 15.11.2017).

11. Иркутский суперкомпьютерный центр СО РАН. URL: http://hpc.icc.ru/ (дата обращения: 15.11.2017).

12. Багдасаров Г.А., Дьяченко С.В., Ольховская О.Г. Измерение производительности и масштабируемости программного комплекса MARPLE3D // Препринты ИПМ им. М.В. Келдыша. – 2012. – № 37. – 22 с. URL: http://library.keldysh.ru/preprint.asp?id=2012-37.

13. Kishimoto A. Fukunaga A., Botea A. Evaluation of a simple, scalable, parallel best-first search strategy // Artificial Intelligence. – 2013. – V. 195. – P. 222–248.

14. Богданова В.Г., Горский С.А., Пашинин А.А. Сервис-ориентированные инструментальные средства для решения задач булевой выполнимости // Фундаментальные исследования. – 2015. – № 2–6. – С. 1151–1156.

15. Bychkov I.V., Oparin G.A., Bogdanova V.G., Pashinin A.A., Gorsky S.A. Automation Development Framework of Scalable Scientific Web Applications Based on Subject Domain Knowledge // Lecture Notes in Computer Science. – 2017. – Vol. – 10421. – P. 278–288.

Парадигма сервис-ориентированных вычислений активно используется в настоящее время для стандартизации доступа, интеграции и координирования слабосвязанных программных систем посредством создания дополнительного уровня web-сервисов на основе существующих научных приложений [1]. Такая тенденция актуализирует разработку инструментальных средств автоматизации создания и поддержки функционирования сервис-ориентированных параллельных приложений пользователя, выполняющихся в распределенной гетерогенной вычислительной среде. Разработка таких программных средств ориентирована как на повышение скорости решения задачи пользователя, так и на увеличение ее размерности. Масштабируемость приложения является одним из основных требований, предъявляемых к программной разработке. В настоящей статье под масштабируемостью будем понимать свойство параллельной программы, характеризующее зависимость изменения динамических характеристик ее работы от изменения параметров запуска этого приложения [2]. Цель работы заключается в исследовании масштабируемости разработанного сервис-ориентированного приложения для решения обладающих высокой вычислительной сложностью задач булевой выполнимости, предназначенного для применения при проведении фундаментальных и прикладных исследований, имеющих дело с отображениями, области определения и значений которых лежат в пространствах векторов с двоичными компонентами 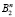(B2 = {0, 1}) [3]. Булевы модели представлены в конъюнктивной нормальной форме (КНФ).

Для оценки масштабирования использован предложенный в работе [2] подход, рассматривающий масштабируемость приложения как многомерную функцию от большого числа параметров запуска. Приведенная в [2] методика получения оценки масштабируемости, учитывающая зависимость эффективности приложения от параметров запуска, применена при исследовании качества работы приложения для различных классов задач булевой выполнимости. В дополнение к исследованию зависимости от количества процессов и размерности задачи для класса случайных 3КНФ анализируется влияние третьего параметра (нагрузки на дочерние процессы MPI-приложения).

Постановка задачи

Задача булевой выполнимости («выполнимости КНФ» или «задача SAT») есть, по существу, задача распознавания совместности системы уравнений [4]

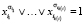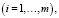, (1)

где переменная

, .

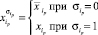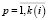Требуется найти решение системы (1) либо установить ее несовместность.

В работе [3] приведен обзор исследований по разработке технологий, методов и средств параллельного решения задач SAT для различных типов архитектур многопроцессорной техники. В зависимости от реализуемого подхода в многообразии современных параллельных программных средств решения этой задачи можно выделить два семейства – решатели, использующие кооперацию, и решатели, использующие конкуренцию. В настоящей работе исследуется масштабируемость сервис-ориентированного приложения, реализованного на основе разработанного авторами решателя hpcsat [5], относящегося к первому семейству.

Параллельный решатель

Массовый параллельный решатель hpcsat представляет собой MPI-приложение на языке C++ и предназначен для параллельного решения ресурсоемких задач булевой выполнимости большой размерности на вычислительных кластерах с SMP узлами. Решатель hpcsat реализован на основе метода полного поиска и использует параллелизм по данным. Главный процесс приложения организует динамическую очередь подзадач, получаемых в результате декомпозиции исходной булевой модели методом расщепления [6]. В дочернем процессе может выполняться как многопоточное, так и однопоточное приложение. В качестве таких приложений используются параллельные, реализованные с использованием технологии работы с общей памятью, и последовательные SAT решатели. Запускаемые в дочернем потоке sat-решатели называются базовыми. Они предназначены для определения выполнимости остаточной функции, полученной в результате расщепления исходной булевой функции. В дочернем потоке также запускаются и программы препроцессорной обработки остаточной булевой функции, упрощающие функцию путем применения правил преобразования, используемых в DPLL-алгоритмах – удаления единичных дизъюнктов, чистого литерала, резолюции и т.д. [7].

Остаточные булевы функции после препроцессорной обработки могут оказаться существенно отличающимися по вычислительной сложности. Поэтому главный процесс регулирует загрузку дочерних процессов, чередуя отправление заданий на упрощение и решение остаточных функций в ответ на запрос дочернего процесса, в зависимости от состояния очереди и дерева расщепления. Описание алгоритма hpcsat приведено в работе [5]. Пользователю предоставляется возможность установки опциональных параметров запуска приложения – количества процессоров, размера блока подзадач для дочернего процесса (нагрузка дочернего процесса), эвристики расщепления, глубины расщепления и базового решателя, запускаемого в дочернем процессе.

Для оценки качества работы hpcsat был проведен ряд экспериментов, в которых для определения масштабируемости менялись параметры запуска приложения при решении набора тестовых задач. Для сравнения с hpcsat использовался массовый параллельный решатель HordeSat [8] со свободно предоставляемым кодом.

Вычислительные эксперименты

Для экспериментов были выбраны классическая задача искусственного интеллекта о голубях и клетках [9] и блок случайных 3КНФ, в состав которого входили 200 выполнимых и 200 невыполнимых SAT задач [10]. Время решения одной задачи было ограничено соответственно сорока восемью и тридцатью шестью тысячами секунд. В невыполнимой задаче о голубях и клетках (Hole11, …, Hole15) требуется посадить в n клеток (n + 1)-го голубя так, чтобы в каждой клетке сидел ровно один голубь. За размерность задачи о голубях принимается величина n, при этом количество булевых переменных равняется n×(n + 1). В тестовых примерах n = 11, …, 15. Размерность случайных 3КНФ определяется количеством булевых переменных.

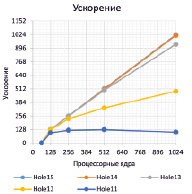
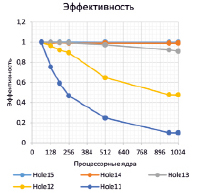
Рис. 1. Ускорение и эффективность hpcsat при решении задачи о голубях и клетках

Задачи решались на вычислительном кластере «Академик В.М. Матросов» [11]. Отличительными особенностями выполнимых SAT задач является, во-первых, то, что подзадачи, полученные при декомпозиции по данным, могут существенно отличаться по структуре и по времени выполнения в зависимости от тех переменных, по которым происходило расщепление исходной функции. Во-вторых, при нахождении выполняющего набора при решении одной из подзадач остальные снимаются со счета. Это обстоятельство объясняет ситуации, когда задача большей размерности при равных ресурсных возможностях решается быстрее. Эксперименты были проведены для получения времени решения на разном количестве ядер для задач разной размерности.

Анализ результатов

Полученные экспериментальные результаты оценивались следующим образом:

- проведено вычисление характеристик ускорения и эффективности;

- проведено вычисление метрик масштабируемости по методике [2];

- применена расширенная методика для случайных 3КНФ.

Ускорение (S) и эффективность (E) вычислялись по формулам

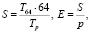
где T64 и Tp – время решения задачи на 64-х и на p процессорных ядрах соответственно. За единицу принимаются 64 процессорных ядра, так как это минимальное количество, на котором мог быть решен ряд тестовых задач в пределах допустимого интервала времени. Такой подход при оценке ускорения и эффективности применяется достаточно часто (например, [12, 13]) и объясняет незначительное превышение единичного уровня эффективности в вычислениях [12]. Изменения ускорения и эффективности для задачи о голубях, характеризующие масштабируемость разработанного параллельного приложения hpcsat при решении этой задачи, приведены на рис. 1. По рисунку видно, что при увеличении размерности и количества процессорных ядер ускорение становится линейным, а эффективность близка к единице, что показывает хорошую масштабируемость hpcsat.

Вычисление метрик масштабируемости

Согласно [2] используются метрики: минимальное и максимальное значения количества процессорных ядер (min (p), max (p)), размерности задачи (min (d), max (d)) и эффективности (max (E), min (E)), величина влияния (вклад) на изменение масштабируемости при увеличении количества процессорных ядер (MarkProcs), размерности задачи (MarkData) и обобщенный вклад (MarkAll). Кратко опишем методику из [2] применительно к анализу влияния на изменение эффективности hpcsat двух параметров запуска (количества процессорных ядер и размерности задачи), изменив немного обозначения для удобства изложения в следующем разделе при описании вычисления метрик для трех параметров. Вся область параметров запуска приложения разбивается на отдельные элементы, эффективность которых представлена вектором

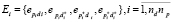, (2)

где pi соответствует количеству процессоров, di – размерности задачи i-того элемента; nd и np – количество значений процессорных ядер и размерностей задач, для которых проводились эксперименты; знак «+», используемый в качестве верхнего индекса, обозначает следующее за pi или di значение. Вычисленные по результатам экспериментальных данных значения эффективности для всех элементов Ei группируются в таблицу в соответствии с [2]. Для каждого элемента вычисляются значения приращений эффективност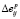и и 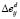по каждому параметру. Остальные метрики вычисляются следующим образом:

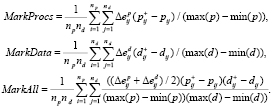(3)

Метрика MarkProcs определяет интенсивность изменения эффективности с увеличением количества процессорных ядер при фиксированной размерности (вычислительной сложности) задачи. Метрика MarkData показывает интенсивность изменения эффективности при увеличении размерности задачи на одном и том же количестве ядер. Метрика MarkAll отражает общее влияние обоих параметров запуска [2].

Оценка масштабируемости для задачи о голубях и клетках

При обработке результатов вычислительных экспериментов для задачи о голубях и клетках получены следующие значения метрик:

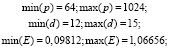
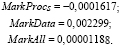
Для задачи о голубях и клетках эффективность постепенно уменьшается с увеличением количества ядер при постоянной сложности задачи, увеличение размерности при фиксированном числе процессорных ядер приводит к увеличению эффективности. Изменение эффективности при одновременном увеличении обоих параметров запуска остается положительным. Эффективность в данном случае зависит от двух величин, т.е. является функцией от количества процессорных ядер и размерности задачи fe(p, d).

В результате аппроксимации экспериментальных данных, представляющих табличное задание функции эффективности, с величиной достоверности аппроксимации R² = 0,928296 получен следующий вид функции:

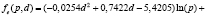
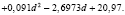(4)

Положив значение функции fe(p, d) равным требуемому уровню эффективности и проведя преобразования, получим выражение, показывающее зависимость размерности задачи от количества процессорных ядер:

,

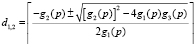где

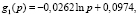
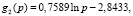
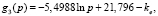
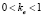– константа, задающая требуемый уровень эффективности; p = 64,65,… – количество процессорных ядер (начинает изменяться от 64, так как это значение является условной единицей – наименьшим количеством ядер, начиная с которого проводились эксперименты). Подставив значение ke и p в формулу, получим нижнее и верхнее значения размерности задачи, при которых сохраняется (приблизительно) требуемый уровень эффективности. При включении в формулу (4) (в правую часть в качестве дополнительных слагаемых рMarkProas + dMarkData + pdMarkAll) приведенных выше метрик точность аппроксимации улучшается до R² = 0,99988. Соответствие поверхностей (построенной по экспериментальным данным и заданной функцией fe(p, d)) приведено на рис. 2.

Таким образом, повышение размерности обеспечивает требуемый уровень эффективности при увеличении количества процессорных ядер для регулярной SAT задачи.

На рис. 3 приведены результаты, показывающие значительно лучшее (меньшее) время решения задачи о голубях решателем hpcsat в сравнении с HordeSat. Решить с помощью HordeSat задачи Hole14 и Hole15 за приемлемое время не удалось.

Оценка масштабируемости для случайных 3КНФ

Обобщенные результаты решения тестовых 3КНФ задач приведены в табл. 1. Решатель HordeSat не справился с рядом невыполнимых SAT задач за отведенное для тестирования время выполнения на одну задачу (36000 секунд). Рассмотрим факторы влияния на эффективность решения таких задач для hpcsat.

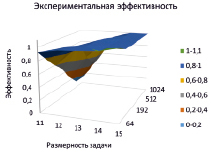
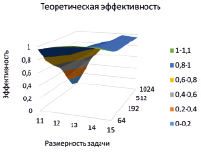
Рис. 2. Зависимость эффективности hpcsat от двух параметров запуска, размерности задачи (ось x) и количества процессорных ядер (ось y)

Таблица 1

Статистика выполнения тестовых 3КНФ (время приведено в секундах)

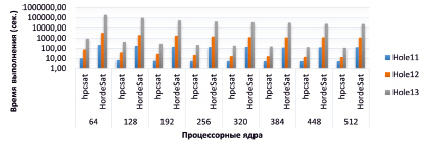
Рис. 3. Время решения задачи о голубях и клетках для n = 11, 12, 13

Для рассматриваемых задач время решения превышало 1500 секунд на 64 процессорных ядрах. В качестве динамических характеристик при оценке масштабируемости hpcsat использовались количество процессорных ядер и размерность задачи. Результаты вычисления метрик с разным значением нагрузки l для решателя hpcsat приведены в табл. 2. Значения метрик, характеризующих область, на которой производились оценки, следующие:

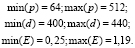
Таблица 2

Изменение эффективности в зависимости от p и d при разной нагрузке для невыполнимых SAT задач

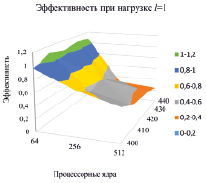
По результатам, приведенным в таблице, видно, что с увеличением количества процессорных ядер и размерности эффективность постепенно снижается. Увеличение нагрузки уменьшает снижение эффективности. При l = 64 увеличение количества процессорных ядер повышает эффективность, при этом уменьшение эффективности, определяемое метриками MarkData и MarkAll, снижается (рис. 4). По рисунку видно, что действительно, увеличение нагрузки повышает эффективность. Так, если при l = 1 наблюдалось ее снижение до уровня 0,2–0,4 (рис. 4. а), то при l = 4 наименьшая эффективность возрастает до 0,4–0,6 (рис. 4, б), при l = 16 этот уровень почти пропадает (рис. 4, в), при l = 64 эффективность в основном держится на уровне 0,8–1 (рис. 4, г).

Введем в примененную выше методику [2] дополнительный расчет метрики MarkLoad, показывающей интенсивность и направление изменения эффективности в границах рассматриваемых параметров по направлению увеличения нагрузки l на дочерний процесс – размер блока подзадач. Тогда вектор (1) будет содержать следующие компоненты:

,

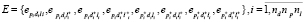где nl – количество значений нагрузки. При вычислении метрик приращение 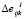будет вычисляться аналогично приращениям количества процессорных ядер 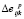и размерности задачи 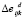. Остальные метрики (с соответствующими изменениями в (3)) будут вычисляться по следующим формулам:

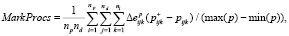
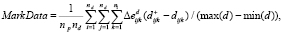
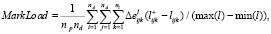
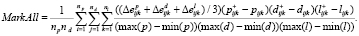
В результате получим общее снижение эффективности MarkAll на два порядка меньше по сравнению с результатами, приведенными в табл. 2:

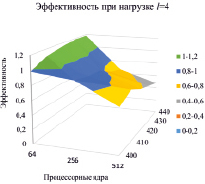
а) нижний уровень 0,2–0,4 б) нижний уровень 0,4–0,6

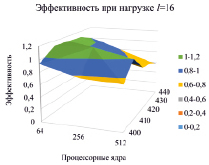
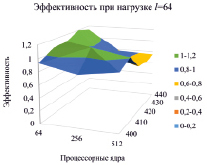
в) процент уровня 0,4–0,6 уменьшился г) нижний уровень 0,6–0,8

Рис. 4. Изменение эффективности при увеличении количества ядер от 64 до 512 (ось x) для невыполнимых 3КНФ размерности от 400 до 440 (ось y) при разной нагрузке на дочерние процессы

Оценку метрик масштабируемости HordeSat для этого класса задач на рассматриваемом интервале получить не удалось, так как на 256 процессорных ядрах была решена только часть задач, на 512 ядрах – ни одной.

Тестирование показало, что для выполнимых 3КНФ, наоборот, лучшие результаты получаются при единичной нагрузке. В этом случае вместо избыточности подзадач в hpcsat используется параметр, регулирующий выравнивание по размеру остаточных КНФ, получаемых при расщеплении исходной булевой функции. Более подробное изложение оценки влияния этого параметра представляет собой материал для описания следующего исследования. В данной статье приведем сравнительную оценку hpcsat и HordeSat на всем наборе случайных выполнимых 3КНФ с использованием метрик без учета этого параметра (табл. 3).

Таблица 3

Оценки зависимости эффективности от p и d для выполнимых 3КНФ

Остальные метрики области параметров запуска имеют следующие значения:

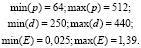
При решении случайных выполнимых 3КНФ эффективность довольно быстро начинает уменьшаться при увеличении как количества процессоров, так и размерности задачи. Накладные расходы HordeSat, понижающие эффективность, связаны с обменом наборами конфликтных дизъюнктов. Решатель hpcsat не использует такой обмен, однако время выполнения зависит от того, когда из очереди запустится подзадача, содержащая решение, тем не менее эффективности hpcsat для данного класса задач несколько лучше.

В целом на основании представленных оценок можно сделать вывод о достаточно хорошей масштабируемости hpcsat, особенно при решении SAT задач, имеющих регулярную структуру, когда булева модель задана аналитически. На основе решателя hpcsat разработан сервис для решения задач булевой выполнимости [14]. Таким образом, обеспечивается свойство горизонтальной масштабируемости при работе в распределенной вычислительной среде (РВС). Интеграция с дополнительным вычислительным узлом, включаемым в эту среду, для использования его ресурсов осуществляется путем установки на этот узел конфигурируемого hpcsomas-агента [15].

Заключение

Выполнена оценка масштабируемости разработанного массового параллельного решателя hpcsat. Выявлены параметры запуска решателя, влияющие на эффективность решения SAT задач трех классов – невыполнимых задач, имеющих регулярную структуру, случайных выполнимых и невыполнимых 3КНФ. Проведено сравнение с существующим параллельным SAT решателем, подтверждающее эффективность hpcsat.

Исследование выполнено при поддержке РФФИ, проект № 15-29-07955-офи_м.

Библиографическая ссылка