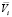В настоящее время для получения воды высокого качества для различных целей широко используются обратноосмотические установки, для успешной эксплуатации которых требуется предварительная очистка воды на микрофильтрах [1]. Микрофильтры выполняются из различных материалов, на сегодняшний день широкое распространение получили фильтрующие элементы из нетканого полимерного материала [2].
Основными характеристиками фильтрующих элементов являются эффективность и грязеемкость. Обеспечение требуемых характеристик эффективности и максимальной грязеемкости установок микрофильтрации является необходимым условием для успешной работы установок обратного осмоса [3].
Целью работы являлась разработка методики расчета параметров фильтрующих элементов из нетканого полимерного материала, позволяющей изготавливать фильтры с оптимальными характеристиками по грязеемкости, перепаду давлений и тонкости фильтрации.
Проведение исследования и оборудование
Для проведения расчета параметров работы фильтрующих элементов из нетканого полимерного материала предварительно проведено исследование их строения и определены основные технологические характеристики работы.
Исследование строения фильтрующего элемента микрофильтра
Объектом исследования являлся фильтрующий элемент для очистки жидкостей от механических примесей, изготовленный по технологии близкой к «meltblown», но имеющей свои особенности, которые позволяют более гибко регулировать параметры поровой структуры фильтрующего слоя (рис. 1).

Рис. 1. Внешний вид фильтрующего элемента
Структура исследуемого фильтрующего элемента состоит из подложки, «отсечного» слоя и фильтрующего слоя.
Каркас обеспечивает геометрическую целостность слоя фильтрующего материала, который в процессе фильтрации испытывает значительные нагрузки из-за разности гидравлических давлений жидкости на входе и выходе фильтрующего элемента. На поверхность каркаса наносится тонкий слой фильтрующего материала – подложка. Данный слой предотвращает миграцию волокон фильтрующего материала в отфильтрованную жидкость.
«Отсечной» слой обеспечивает необходимую тонкость фильтрации и отвечает за параметры эффективности фильтрующего элемента.
Последний слой фильтрующего материала несет на себе основную нагрузку по очистке жидкости. Он имеет наибольшую толщину, которая определяется наружным диаметром фильтрующего элемента. Размер пор плавно увеличивается от «отсечного» слоя до наружного (фильтрующего). Закон изменения размера пор зависит от гранулометрического состава твердых частиц в фильтруемой жидкости и должен выбираться из условия обеспечения максимальной грязеемкости фильтрующего элемента [4].
Проведение расчета параметров фильтрующего слоя
Критерием оптимальности структуры фильтрующего элемента является его максимальная грязеемкость при заданном гранулометрическом составе твердых частиц в фильтруемой жидкости [5].
За основу в разрабатываемой методике расчета параметров фильтрующего слоя взято положение о том, что для достижения максимальной грязеемкости в процессе фильтрации, частицы загрязнений должны равномерно заполнять поры фильтрующего материала. Для этого необходимо, чтобы объемы пор заданных размеров равнялись объемам твердых частиц соответствующих размеров.

Рис. 2. Лабораторный стенд контроля качества фильтров для жидких сред

Рис. 3. Счетчик частиц PAMAS S-4031 WG
Гранулометрический состав кварца молотого пылевидного
|
Размер частиц |
Количество частиц заданного размера |
Объем частиц заданного размера Vi |
Относительный объем частиц заданного размера |
|
мкм |
шт. |
м3 |
% |
|
1,25 |
3248105 |
3,32E-12 |
1,51 |
|
1,75 |
1276588 |
3,58E-12 |
1,63 |
|
2,25 |
616211 |
3,68E-12 |
1,67 |
|
2,75 |
328673 |
3,58E-12 |
1,63 |
|
3,25 |
217495 |
3,91E-12 |
1,78 |
|
3,75 |
201102 |
5,55E-12 |
2,53 |
|
4,25 |
195107 |
7,84E-12 |
3,57 |
|
5,00 |
224536 |
1,47E-11 |
6,70 |
|
5,75 |
45278 |
4,51E-12 |
2,05 |
|
6,50 |
56418 |
8,11E-12 |
3,70 |
|
7,50 |
41463 |
9,16E-12 |
4,17 |
|
9,00 |
40831 |
1,56E-11 |
7,10 |
|
11,00 |
22150 |
1,54E-11 |
7,03 |
|
13,50 |
14319 |
1,84E-11 |
8,41 |
|
16,50 |
6525 |
1,53E-11 |
6,99 |
|
19,50 |
3282 |
1,27E-11 |
5,81 |
|
23,00 |
2162 |
1,38E-11 |
6,28 |
|
27,50 |
1194 |
1,30E-11 |
5,92 |
|
32,50 |
542 |
9,74E-12 |
4,44 |
|
37,50 |
262 |
7,23E-12 |
3,30 |
|
42,50 |
154 |
6,19E-12 |
2,82 |
|
47,50 |
78 |
4,38E-12 |
1,99 |
|
55,00 |
79 |
6,88E-12 |
3,14 |
|
65,00 |
36 |
5,18E-12 |
2,36 |
|
75,00 |
18 |
3,98E-12 |
1,81 |
|
85,00 |
7 |
2,25E-12 |
1,03 |
|
95,00 |
3 |
1,35E-12 |
0,61 |
|
∑Vi = 2,19E-10 |
100,00 |
Исходными данными для расчета параметров фильтрующего слоя являлись сведения о гранулометрическом составе твердых частиц в фильтруемой жидкости. В качестве загрязнителя использовался кварц молотый пылевидный марки Б ГОСТ 9077-82 [4].
Гранулометрический состав загрязнителя определялся на лабораторном стенде (рис. 2).
В емкость объемом 3 л набиралась чистая вода, добавлялся загрязнитель. Затем загрязненная вода подавалась на фильтрующий элемент и отбиралась проба воды до и после него с помощью пробоотборников.
Количество частиц загрязнителя в пробе воды определялось с помощью счетчика частиц (рис. 3).
Используя серию замеров, был определен гранулометрический состав загрязнителя; результаты представлены в табл. 1. В данной таблице представлены также результаты расчета объема частиц загрязнителя в предположении, что все они имеют сферическую форму. В последнем столбце таблицы приведены относительные объемы частиц по всем размерам, вычисленные по формуле
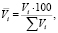 (1)
(1)
где Vi – объем частиц заданного размера, м3; ∑Vi – суммарный объем частиц в принятом интервале размеров, м3.
По относительному объему частиц заданного размера был выделен объем фильтрующего материала, пропорционально объему частиц и определены интервалы диаметров, обуславливающие положение данного объема фильтрующего материала в фильтрующем элементе.
Для вычислений использовалось поперечное сечение фильтрующего элемента (рис.4), с указанием основных геометрических размеров.
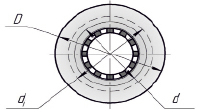
Рис. 4. Сечение фильтрующего элемента
Здесь d – внутренний диаметр, мм; D – наружный диаметр фильтрующего слоя, мм; di – размер, определяющий положение рассматриваемого элемента фильтрующего материала, мм.
Для дальнейших расчетов использована система уравнений (2), в которой относительные объемы твердых частиц заменены на эквивалентные им значения площадей элементов поперечного сечения фильтрующего слоя.
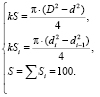 (2)
(2)
Из первого уравнения системы получен коэффициент пропорциональности k. Он представлен в виде формулы
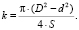 (3)
(3)
Подставив формулу (3) во второе уравнение системы, получим выражение
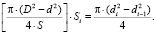 (4)
(4)
Из формулы (4) были определены значения диаметров di по формуле (5):
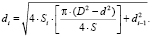 (5)
(5)
Толщина рассматриваемого фрагмента фильтрующего слоя определялась по формуле
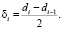 (6)
(6)
В результате проведенных вычислений была получена зависимость среднего размера пор фильтрующего материала от диаметра фильтрующего элемента (рис. 5).
При этом принимали в качестве допущения, что средний размер пор равен среднему размеру частиц.
Для изготовления фильтрующего элемента с заданным законом изменения размера пор по толщине фильтрующего слоя необходимо было получить связь между технологическими параметрами оборудования и параметрами фильтрующего слоя. Основным технологическим параметром, который определяет размер пор в фильтрующем материале, является давление воздуха на регуляторе. Для фильтрующего слоя таким параметром является удельное воздушное сопротивление воздушному потоку.
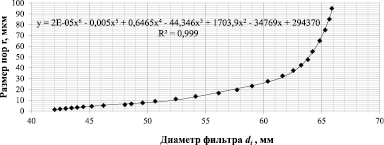
Рис. 5. График зависимости среднего размера пор r фильтрующего материала от диаметра di
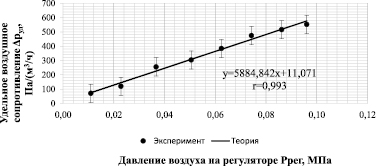
Рис. 6. Экспериментальная и теоретическая зависимости удельного воздушного сопротивления фильтрующего слоя от давления воздуха на регуляторе
Для определения воздушного сопротивления элементов фильтрующего слоя использована зависимость (7), полученная для образцов «отсечного» слоя с номинальной тонкостью фильтрации.
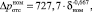 (7)
(7)
где δном – номинальная тонкость фильтрации, мкм.
С учетом принятых обозначений удельное воздушное сопротивление элементов фильтрующего слоя, Па/(м3/ч), определялось по формуле
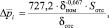 (8)
(8)
где δотс – толщина «отсечного» слоя, исходя из проведенных испытаний, равна δотс = 3 мм; Sотс – площадь фильтрующего материала на «отсечном» слое, м2, определялась по формуле
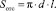 (9)
(9)
Для испытанных ранее нами образцов [4] и в данной работе длина «отсечного» слоя принималась равной l = 40 мм, а диаметр d = 39 мм.
Удельное воздушное сопротивление с учетом данных, представленных выше, было определено по формуле
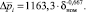 (10)
(10)
Удельное сопротивление фильтрующего материала связано с давлением воздуха на регуляторе определенной зависимостью. В диапазоне давлений от 0,005 МПа до 0,1 МПа эту зависимость можно принять линейной.
На рис. 6 представлена полученная экспериментальная зависимость удельного воздушного сопротивления фильтрующего слоя от давления воздуха на регуляторе, подтверждающая возможность такого допущения. Также на нем представлена теоретическая зависимость данных параметров, полученная с помощью метода наименьших квадратов.
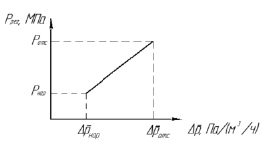
Рис. 7. Линейная зависимость давления воздуха на регуляторе от удельного сопротивления фильтрующего материала
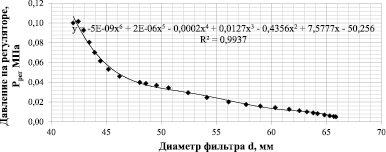
Рис. 8. График зависимости расчетного давления воздуха на регуляторе от диаметра фильтра
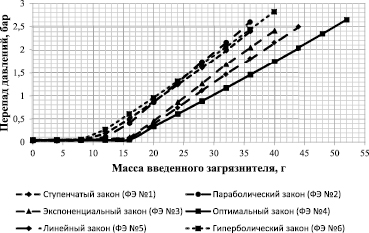
Рис. 9. Характеристики грязеемкости образцов с различными структурами
Задаваясь двумя точками (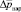 ; Рнар) и (
; Рнар) и (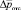 ; Ротс) на рис. 7, получена зависимость для давления воздуха на регуляторе, описываемая формулой
; Ротс) на рис. 7, получена зависимость для давления воздуха на регуляторе, описываемая формулой
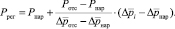 (11)
(11)
Определив значения давления воздуха на регуляторе по формуле (11), получен искомый график зависимости расчетного давления воздуха на регуляторе Ррег от диаметра фильтра di (рис. 8).
Приведенная методика расчета позволяет определять структуру фильтрующего элемента с оптимальными характеристиками по эффективности и грязеемкости. Фильтрующий элемент, изготовленный по полученной зависимости, обладает наибольшей грязеемкостью.
Экспериментальное подтверждение приведенной методики
Для сравнительных испытаний на грязеемкость был проведен расчет структур нескольких фильтрующих элементов, у которых закон изменения давления на регуляторе отличался от оптимального. Использовались следующие законы изменения давления воздуха на регуляторе от диаметра фильтрующего элемента: ступенчатый, параболический, экспоненциальный, линейный, гиперболический. С помощью проведенных расчетов изготовили 6 партий фильтрующих элементов, в каждой из которых было по 5 образцов.
Результаты ресурсных испытаний, проведенных на гидравлическом стенде, представлены на рис. 9.
По сводному графику (рис. 9) видно, что фильтрующий элемент № 4, который был изготовлен нами на предприятии в соответствии с разработанной методикой расчета фильтрующего слоя, имеет наибольшую грязеемкость среди всех испытанных образцов.
В ходе анализа данных получили, что грязеемкость фильтрующего элемента увеличилась на 36 % по сравнению с применяемым в настоящее время на производстве фильтроэлементом, сформированным по ступенчатому закону.
- В результате проведенного исследования получена зависимость удельного воздушного сопротивления фильтрующего материала от давления воздуха на регуляторе. Проведенные испытания позволили сделать вывод о том, что данную зависимость можно принять линейной.
Разработанная методика расчета параметров фильтрующих элементов в дальнейшем может быть использована при изготовлении фильтров с оптимальными характеристиками по грязеемкости, перепаду давлений и тонкости фильтрации для заданных условий эксплуатации.
Библиографическая ссылка
Христофорова М.И., Хролынцев А.А., Яковлева О.В. МЕТОДИКА РАСЧЕТА ОПТИМАЛЬНОЙ СТРУКТУРЫ ФИЛЬТРУЮЩЕГО ЭЛЕМЕНТА ИЗ НЕТКАНОГО ПОЛИМЕРНОГО МАТЕРИАЛА // Фундаментальные исследования. 2017. № 11-2. С. 331-337;URL: https://fundamental-research.ru/ru/article/view?id=41944 (дата обращения: 17.02.2026).