Проведем динамический анализ бруса батана и рапирного механизма металлоткацких станков типа СТР с учетом упругости элементов их привода. Используя методику упрощений, рассмотренную в [1], динамическую модель упругой системы батанного и рапирного механизмов приведем к виду, представленному на рис. 1. Динамическая модель содержит четыре взаимосвязанных контура: I и II – контуры главного и промежуточного валов соответственно (рассматриваем как крутильно-колеблющиеся системы с конечным числом степеней свободы); III – контур бруса батана (рассматриваем как изгибно-колеблющуюся систему с распределенными параметрами); IV – контур рапирного механизма (рассматриваем как крутильно-колеблющуюся систему с конечным числом степеней свободы). Первый, второй и четвертый контуры связаны между собой кулачковой передачей, а второй и третий – рычажной.
На рис. 1 введены следующие обозначения: Ii,j – моменты инерции масс дисков, характеризующие инерционные свойства механизмов; Yб(x, t) – абсолютные перемещения сечений бруса батана; φi,j – абсолютные угловые перемещения дисков (i – номер контура, j – номер диска); EIб – изгибная жесткость бруса; μб – погонная масса бруса; Сi,j – коэффициенты жесткости упругих элементов механизмов; mб – приведенная масса лопасти батана и подбатанного вала; kп – коэффициент, учитывающий упругое сопротивление системы заправки нитей основы на фазе формирования сетки (коэффициент постели); ω – угловая скорость вращения главного вала (в расчетах принимается постоянной величиной); П12, П23 – функции перемещения кулачкового и рычажного механизмов соответственно – П12 = φ22(φ13) = φ2n–1(φ1n–1), П23 = Yб(φ21) = = Yб(φ22) = Yб(φ2n–1) = Yб(φ2n); П14 – переда-точная функция, учитывающая линейную жесткость (Cx) и линейное сопротивление (βк) клиноременной передачи привода – П14 = φ41(φ11), (клиноременная передача привода на рис. 1 не показана). При решении подобных технических задач для упрощения математической модели, используя рекомендации [2], будем считать, что деформируемые элементы батанного и рапирного механизмов являются идеально упругими, то есть они не характеризуются диссипативными свойствами. Тогда движение упругой системы этих механизмов можно представить в виде следующих дифференциальных уравнений:
контур 1 (главный вал)
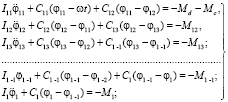(1)
контур 2 (промежуточный вал)
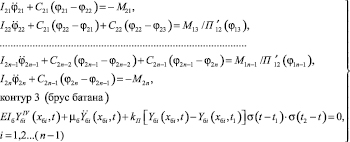(2)
контур 4 (рапирный механизм – считаем, что все звенья рапирного механизма являются абсолютно жесткими и учитываем податливость только клиноременной передачи привода)
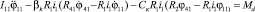. (3)
В уравнениях (1)…(3) приняты следующие обозначения: M12, M13,…, M1n–1, M1n – моменты сопротивления, оказывающие воздействие на главный вал станка со стороны промежуточного вала; M1n – момент сил сопротивления, действующий со стороны механизмов зевообразования, набора товара, отпуска основы; M21, M22,…, M2n–1, M2n – моменты сопротивления, действующие со стороны батана на промежуточный вал [3];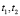 
– периоды времени, соответствующие фазам подхода берда к опушке сетки и отходу от нее; 
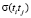– обобщенные функции Хевисайда (единичные функции) [4]; Md – движущий момент на валу двигателя; Mc – момент сопротивления со стороны рапирного механизма, приведенный к валу двигателя.
Системы уравнений (1) и (2) должны соответствовать граничным условиям в краевых сечениях бруса батана и условиям сопряжения участков бруса. Рассмотрим граничные условия и условия сопряжения участков для бруса батана с тремя лопастями, применяемого на металлоткацком станке СТР-130-М, рис. 2.
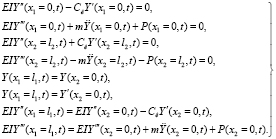(4)
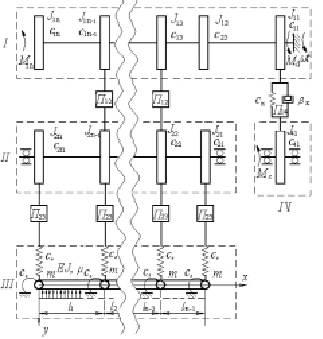
Рис. 1. Динамическая модель кулачково-рычажных батанного и рапирного механизмов при учете упругости элементов привода
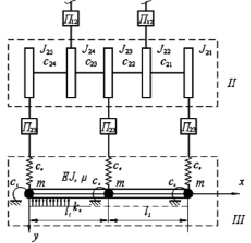
Рис. 2. Динамическая модель трехлопастного кулачково-рычажного батанного механизма при учете упругости элементов привода
В системе (4) обозначено: Cк – приведенная к изгибной крутильная жесткость лопастей батана с учетом жесткости подбатанного вала и его опор; P – усилия, возникающие со стороны привода на сечения бруса батана (характеризуются деформационными параметрами шарнирных соединений рычажной части привода батана).
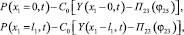
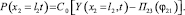(5)
Тогда
,
,
.
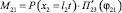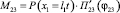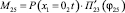Используя относительные координаты, получим
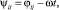i – номер контура; j = 1,…, n – номер контура;
;
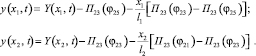(6)
В первой части системы (6) второе и третье слагаемые описывают переносное движение сечений бруса батана. Они учитывают не только кинематическое перемещение бруса, но и перемещение сечений бруса вследствие деформаций звеньев системы привода. В соответствии с рекомендациями [5], функции перемещения П и передаточные функции П' и П" можно аппроксимировать путем разложения их в ряд Тейлора, учитывая только два первых члена ряда
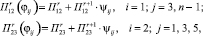(7)
где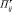 
– функции от кинематических значений параметра φij; r – 0, 1, 2 – порядок производной.
Учитывая выражения (5), (6), (7) и пренебрегая в функциях возмущения малыми членами (второго порядка малости), системы уравнений (1) и (2) представим следующим образом:
для контуров I и II (главный и промежуточный валы)
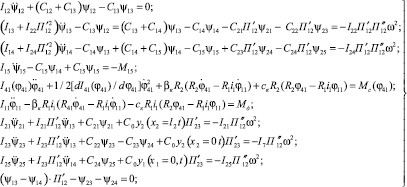(8)
для контура III (бруса батана)
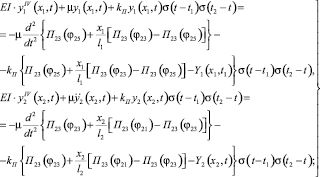(9)
для условий сопряжения участков
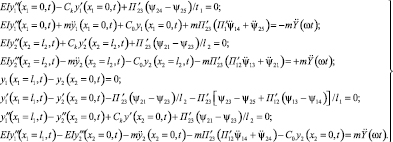(10)
Выражения (8)…(10) являются системой дифференциальных уравнений с переменными коэффициентами. Для решения данной системы воспользуемся методом условного осциллятора [5].
Проанализируем систему однородных уравнений, состоящую из уравнений (8) и (10) с правыми частями равными нулю. Считаем, что частное решение данной системы будет иметь вид аналогичный решению системы с постоянными коэффициентами:
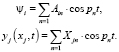(11)
Учитывая выражение (9), уравнение форм изгибных колебаний бруса батана будет иметь следующий вид:
(12)
Далее в рассматриваемую нами систему однородных уравнений подставляем уравнения (11) и (12), т.е. получаем систему алгебраических уравнений в отношении неизвестных амплитуд – Ai, Aj. Затем определитель, составленный из коэффициентов полученной системы, приравняем к нулю, таким образом, получим формальное частное уравнение, из которого определяются зависимости pn(t) корней этого уравнения от времени.
В работе [5] показано, что если соблюдается требование
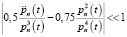, (13)
то рассматриваемую нами систему можно причислить к системам с медленно изменяющимися параметрами. Тогда, применяя метод условного осциллятора [5], запишем решение однородной системы уравнений в следующем виде:
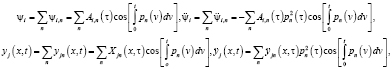(15)
где τ = εt – медленное время; ε – малый параметр. К тому же один из амплитудных коэффициентов для каждой формы, для примера A1n считают равным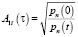 
.
Коэффициенты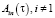 
можно найти, если решение (15) с учетом (12) подставить в систему однородных уравнений, полученную из выражений (8) и (10). Так как A1n(t) и pn(t) известны, то имеющаяся система позволит рассчитать оставшиеся коэффициенты форм упругих колебаний исследуемой динамической модели. Для решения систем уравнений вынужденных колебаний (8) и (9) воспользуемся способом разложения подлежащих нахождению функций в ряд по собственным формам
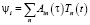, (16)
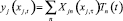. (17)
Обозначим W(x, t) – правую часть первого уравнения системы (9). После преобразований, учитывая выражение (7), имеем
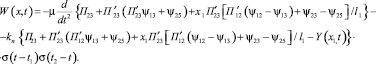(18)
Возмущающую функцию П23(ωt) разложим в ряд по собственным формам колебаний бруса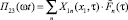 
. Из условия ортогональности нормальных форм получим 
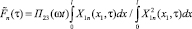, то есть, опуская аргументы в правой части,
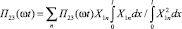. (19)
Соответственно будем иметь
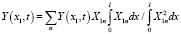. (20)
Принимая во внимание уравнение (12) и что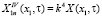 
и подставляя в первое уравнение системы (9) значения (17), (19) и (20) функций П23(ωt) и Y(x1, t), для вычисления неизвестных функций Tn(t) получим выражение
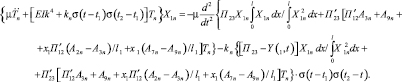(21)
Двукратным дифференцированием соответствующих слагаемых правой части уравнение (21) можно представить в виде
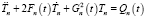. (22)
Выполним в уравнении (22) замену переменных:
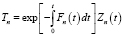. (23)
Проведем подстановку уравнения (23) в (22), после деления на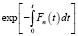 
, имеем
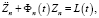(24)
где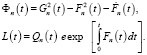 
Представим общее решение уравнения (24) как результат сложения общего решения однородного уравнения
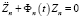(25)
и частного уравнения (24), а именно:
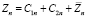(26)
где z1n, z2n – линейно независимые решения уравнения (25);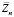 
– частотное решение уравнения (24); C1n, C2n – произвольные постоянные, удовлетворяющие начальным условиям.
Решения уравнения (25) имеют вид
, 
.
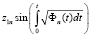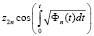Частотное уравнение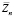 
– можно найти, используя метод вариации произвольных постоянных. Получим
,
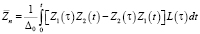где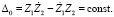 
Решение выражения (26) найдено, значит, найдены и решения уравнений (23) и (25). В соответствии с четвертым уравнением системы (8) имеем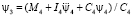 
.
Для рассмотрения учета воздействия технологического сопротивления M4 на колебательный процесс бруса батана функцию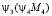 
необходимо подставить в выражение (18), при этом адекватным образом изменится правая часть уравнения (21).
Выводы
Предложена математическая модель решения задачи о вынужденных колебаниях упругой системы батанного и рапирного механизмов металлоткацких станков типа СТР, которая применима к нестационарным условиям работы станка (разгон, установившийся режим с учетом неравномерности вращения главного вала, останов). Данная модель позволит повысить качество анализа влияния колебательных процессов в приводе станка на изгибно-крутильные колебания бруса батана и оценить технологические и конструктивные параметры модернизируемых или проектируемых механизмов.
Библиографическая ссылка
Тувин А.А., Максимов А.А., Аллямов Р.Р. ДИНАМИКА УПРУГОЙ СИСТЕМЫ БАТАННОГО И РАПИРНОГО МЕХАНИЗМОВ МЕТАЛЛОТКАЦКИХ СТАНКОВ ТИПА СТР // Фундаментальные исследования. – 2017. – № 11-1. – С. 133-139;URL: https://fundamental-research.ru/ru/article/view?id=41912 (дата обращения: 16.04.2024).